Глава II. Несобственные интегралы

§1. Несобственные интегралы по неограниченному промежутку

1. Определение несобственного интеграла по неограниченному промежутку

Пусть функция определена на промежутке и интегрируема на любом отрезке .

Определение 1. Несобственным интегралом от функции по бесконечному промежутку (несобственным интегралом 1го рода) называют предел

Если этот предел конечен, то несобственный интеграл называется сходящимся, в противном случае - расходящимся.

Е сли (рис 1), то очевидно, что даёт нам площадь бесконечной криволинейной трапеции.

Принимая во внимание формулу Ньютона-Лейбница и определение несобственного интеграла рода вычислим

,

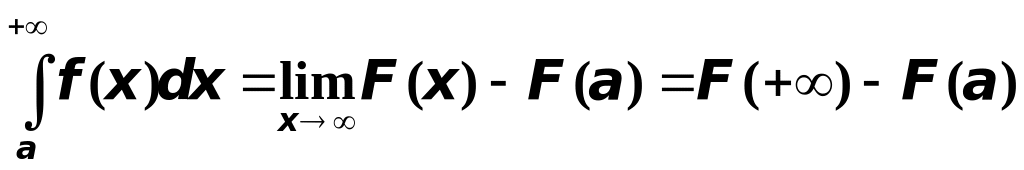где - первообразная функции на любом промежутке . Обобщив формулу Ньютона-Лейбница, можно окончательно написать

,

здесь .

Аналогично определяется и интеграл и его сходимость, т.е.

В том случае, когда бесконечны и верхний и нижний пределы интегрирования, то по определению имеем:

,

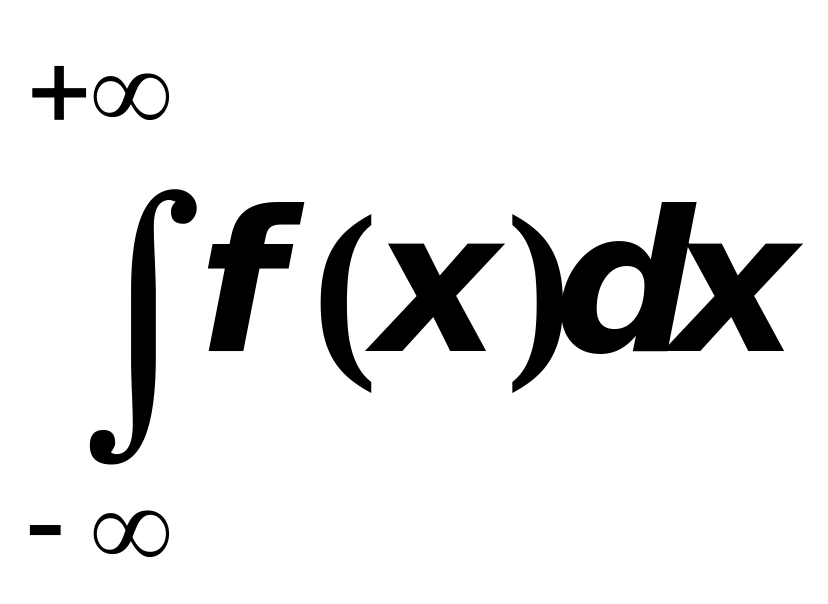где - любое действительное число. При этом несобственный интеграл называется сходящимся, если сходятся оба интеграла, стоящие справа.

2. Главное значение интеграла

Определение. Главным значением несобственного интеграла называется предел

,

которое обозначается так:

(от франц. valleur principal - главное значение)

Заметим, что в определении главного значения несобственного интеграла имеется в виду симметричное возрастание модуля переменной в положительном и отрицательном направлении, в то время как по определению несобственный интеграл мы прежде всего должны заменить суммой

и отдельно исследовать сходимость каждого слагаемого, не накладывая никакой связи на вычисление возникающих при этом несобственных интегралов.

Может оказаться, что несобственный интеграл расходится, а его главное значение сходится.

Очевидно, что для несобственных интегралов справедливы все основные свойства определённого интеграла.

Пример 1. Вычислить

Решение.

Итак, данный интеграл сходится и равен .

Пример 2. Вычислить

Решение. , т.е. данный интеграл расходится.

Пример 3. Исследовать сходимость несобственного интеграла

Решение. , но

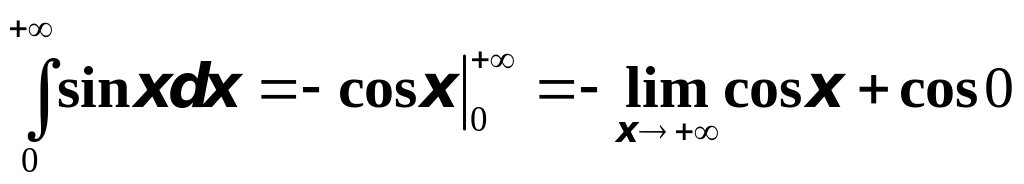
Т.к. не существует, то интеграл расходится, в свою очередь расходится и интеграл , а следовательно можно сделать вывод: данный интеграл расходится.

Рассмотрим теперь 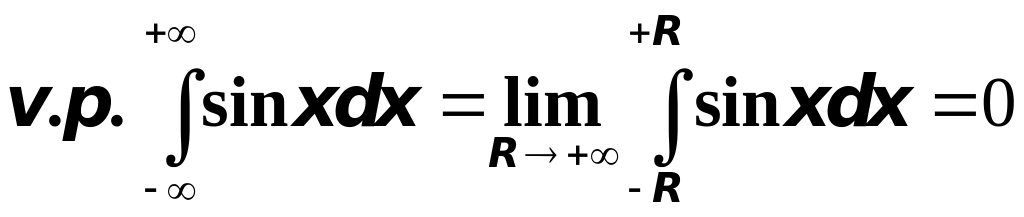, т.к. (как интеграл от нечётной функции по симметричному промежутку).

Ответ: данный интеграл расходится, в то время как его главное значение сходится.

Пример 4. Вычислить, при каком значении параметра несобственный интеграл сходится.

Решение. Ранее мы установили , что при данный интеграл расходится, поэтому при дальнейшем исследовании случай мы рассматривать не будем.

Следовательно

если

т.е.

если

Итак, сходится, если и расходится, если . В дальнейшем этот факт можно использовать как очевидный при решении примеров.

3. Достаточные признаки сходимости несобственных интегралов по неограниченному промежутку

Часто бывает нужно определить, сходится или расходится несобственный интеграл, не находя его первообразной, т.е. оценить сходимость несобственного интеграла. Для этого можно воспользоваться в частности так называемыми признаками сравнения, которые мы оформим в виде теорем.

Теорема 1 (Первый признак сравнения).

Если функции и непрерывны на промежутке и при этом , то тогда

1. если сходится интеграл , то сходится и интеграл ;

2. если интеграл расходится, то расходится и интеграл (рис 2).

Доказательство. Из неравенства

в ытекает 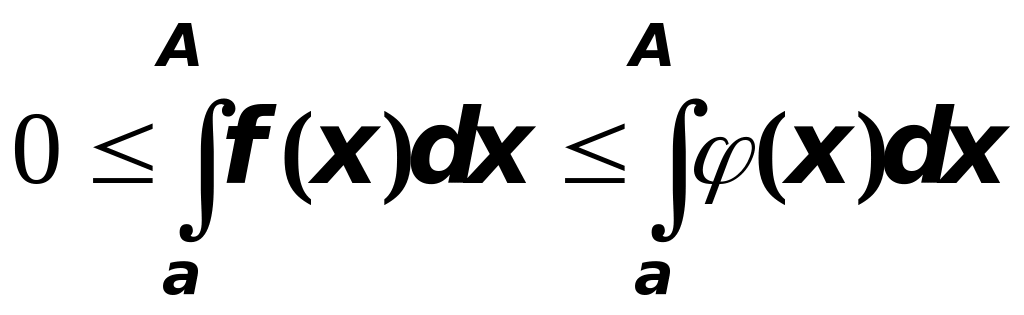, но

т.к. .

Таким образом функция

монотонно возрастает и ограничена сверху, значит существует конечный предел 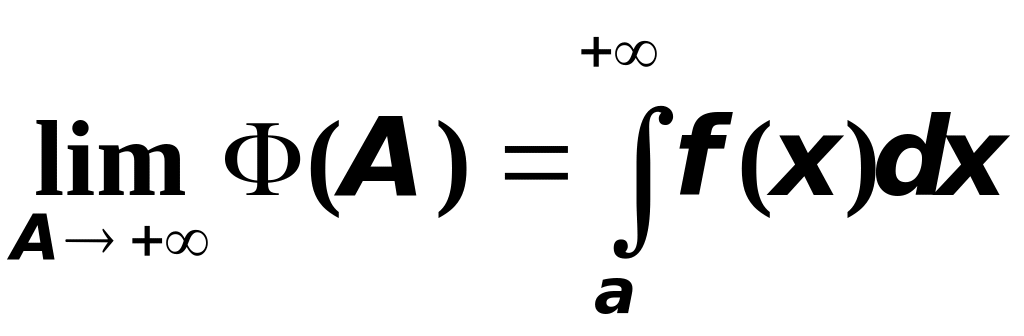, т.е. интеграл сходится.

Пример 5. Оценить сходимость

Решение. Очевидна оценка , а интеграл сходится (см. пример 4, случай ). Следовательно в силу доказанной теоремы сходится.

Пример 6. Исследовать сходимость

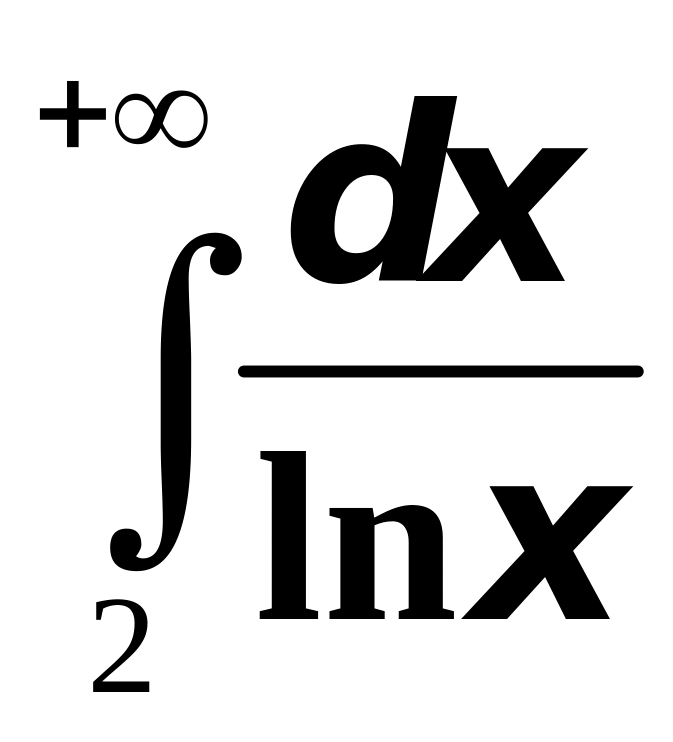
Решение. При , следовательно . Но интеграл , следовательно, расходится и интеграл .

Теорема 2 (Второй признак сравнения).

Если функции и непрерывны на промежутке и неотрицательны, т.е. и , и существует конечный отличный от нуля предел , то тогда интегралы и (где ) в смысле сходимости ведут себя одинаково, т.е. оба сходятся, или оба расходятся.

Доказательство. Допустим, что , причём .

В силу определения предела это означает, что для любого при достаточно больших значениях будет выполнено неравенство , что равносильно или . Предположим сначала, что интеграл сходится, а тогда в силу полученного неравенства и первого признака сравнения следует, что интеграл сходится, значит сходится и .

Допустим теперь, что интеграл расходится, тогда в силу того же неравенства и первого признака сравнения вытекает, что расходится и интеграл , т.е. расходится .