
- •Раздел 1
- •1. Предмет математического программирования
- •1.1. Модель задачи математического программирования
- •1.2. Классификация методов математического программирования
- •2. Линейное программирование
- •2.1. Виды задач линейного программирования
- •Задача о наилучшем использовании ресурсов
- •Задача о раскрое материалов
- •Задача о смесях
- •2.2. Формы записи задач линейного программирования
- •Переход к канонической форме
- •Переход к симметричной форме
- •2.3. Геометрическая интерпретация и графическое решение злп
- •Графический метод решения злп
- •Свойства решений злп
- •Симплексный метод
- •2.5.1. Построение начального опорного плана
- •Нахождение оптимального опорного плана. Переход к нехудшему опорному плану
- •Переход к нехудшему опорному плану
- •3. Двойственность в линейном программировании
- •3.1. Понятие двойственности. Построение двойственных задач
- •Правило построения двойственной задачи
- •Соответствия между неизвестными в паре взаимно двойственных задач
- •Основные теоремы двойственности и их экономическое содержание
Графический метод решения злп
1. С учетом системы ограничений строим область допустимых решений .
2. Строим вектор наискорейшего возрастания целевой функции – вектор градиентного направления.
3. Проводим произвольную линию уровня
(проще всего провести
![]() ,
перпендикулярную к вектору
,
перпендикулярную к вектору
![]() ).
).
4. При решении задачи
на максимум перемещаем линию уровня
в направлении вектора
так, чтобы она касалась области допустимых
решений в ее крайнем положении (крайней
точке). На рисунке выше – это точка
![]() .
В случае решения задачи на минимум линию
уровня
перемещаем в антиградиентном направлении.
На рисунке выше – это точка
.
В случае решения задачи на минимум линию
уровня
перемещаем в антиградиентном направлении.
На рисунке выше – это точка
![]() .
.
5. Определяем оптимальный план
![]() и экстремальное значение целевой функции
.
и экстремальное значение целевой функции
.
В результате решения задачи линейного программирования возможны следующие случаи оптимального плана, которые представлены на рисунке 2.9.


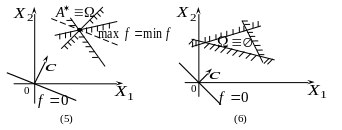
Рис. 2.9.
(1) оптимальный план единственный: линия уровня и область допустимых решений в разрешающем положении имеют одну общую точку;
(2) оптимальных планов бесчисленное множество: в разрешающем положении линия уровня проходит через сторону области допустимых решений;
(3), (4) целевая функция не ограничена: линия уровня, сколько бы ее не перемещали, не может занять разрешающего положения; только в случае (3) возможно решение задачи на минимизацию целевой функции;
(5) область допустимых решений состоит из единственной точки, где целевая функция достигает одновременно и максимального, и минимального значений;
(6) задача не имеет решения: область допустимых решений – пустое множество, т.е. система ограничений задачи несовместна.
Пример 2.5. Решить ЗЛП
![]()
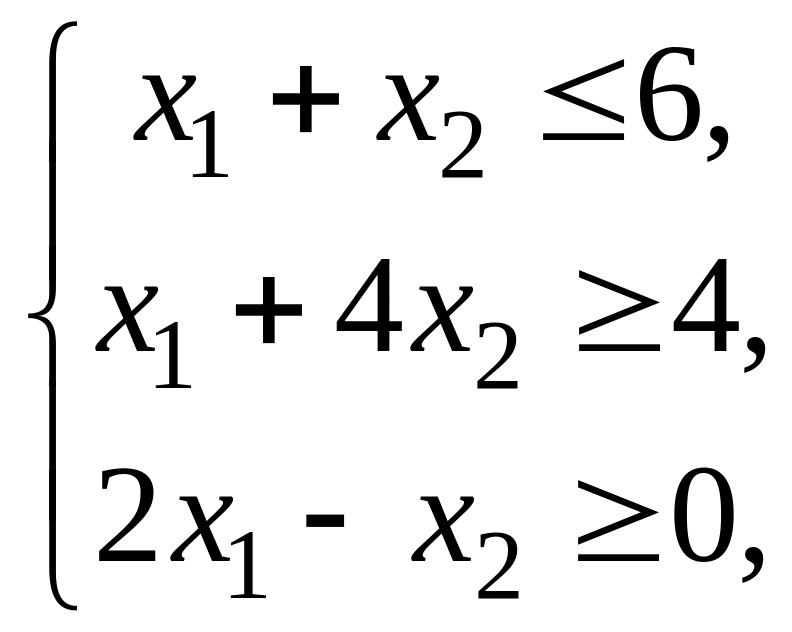
.
Решение. Для построения области допустимых решений строим в системе соответствующие данным ограничениям-неравенствам граничные прямые:
![]() .
.
Находим полуплоскости, в которых
выполняются данные неравенства. Для
этого вследствие выпуклости любой
полуплоскости достаточно взять
произвольную точку, через которую не
проходит соответствующая граничная
прямая, и проверить, удовлетворяет ли
эта пробная точка ограничению-неравенству.
Если удовлетворяет, то данное неравенство
выполняется в полуплоскости, содержащей
пробную точку. В противном случае берется
полуплоскость, не содержащая пробной
точки. В качестве пробной точки часто
удобно брать начало координат
![]() .
Для нашего примера область допустимых
решений – множество точек четырехугольника
ABCD, рис 2.10.
.
Для нашего примера область допустимых
решений – множество точек четырехугольника
ABCD, рис 2.10.

Координаты точки C можно найти из решения системы
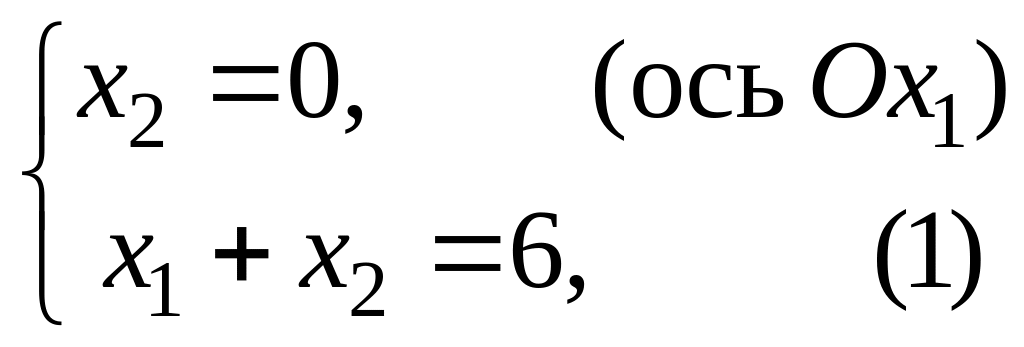
откуда
![]() .
.
Таким образом,
![]() .
.
Ответ: .
Пример 2.6. При производстве продукции
![]() и
и
![]() используют четыре группы оборудования
используют четыре группы оборудования
![]()
![]() и
и
![]() .
На выпуск единицы продукции
расходуется 1; 0,5; 2 и 0 ед. времени
оборудования
и
соответственно, а на выпуск продукции
– 1; 1; 0 и 2 ед. времени оборудования. Фонд
рабочего времени оборудования группы
составляет 18 ед. времени;
.
На выпуск единицы продукции
расходуется 1; 0,5; 2 и 0 ед. времени
оборудования
и
соответственно, а на выпуск продукции
– 1; 1; 0 и 2 ед. времени оборудования. Фонд
рабочего времени оборудования группы
составляет 18 ед. времени;
![]() – 12 ед.;
– 24 ед. и
– 18 ед. Предприятие реализует единицу
продукции
по цене 40 ден. ед.,
– 60 ден. ед.
– 12 ед.;
– 24 ед. и
– 18 ед. Предприятие реализует единицу
продукции
по цене 40 ден. ед.,
– 60 ден. ед.
1) Построить экономико-математическую модель задачи.
2) Графическим методом найти план выпуска продукции, при котором выручка предприятия будет максимальной.
Решение.
1) Запишем условие задачи в виде таблицы.
Вид оборудования |
Продукция |
Фонд рабочего времени, ед. |
|
|
|
||
A B С D |
1 0,5 2 0 |
1 1 0 2 |
18 12 24 18 |
Цена единицы продукции, ден. ед. |
40 |
60 |
|
Пусть объем выпускаемой продукции вида , объем выпуска продукции , т.е. план выпуска продукции предприятием. Прибыль, которую получает предприятие от реализации продукции, стремиться максимизировать, т.е. целевая функция имеет вид
![]() .
.
На производство двух видов продукции
будет затрачено
![]() единиц времени оборудования группы
;
единиц времени оборудования группы
;
![]() оборудования группы
;
оборудования группы
;
![]() оборудования
;
оборудования
;
![]() оборудования
.
При этом, учитывая фонд рабочего времени
каждого вида оборудования, получаем
систему ограничений:
оборудования
.
При этом, учитывая фонд рабочего времени
каждого вида оборудования, получаем
систему ограничений:

По содержанию задачи переменные .
Таким образом, получаем следующую математическую модель, которая является задачей линейного программирования.
![]() ,
,

.
2) Так как план выпуска продукции содержит две переменные, то ЗЛП можно решить графическим способом.
Для построения области допустимых решений строим в системе координат соответствующие данным ограничениям-неравенствам граничные прямые, рис. 2.11.:
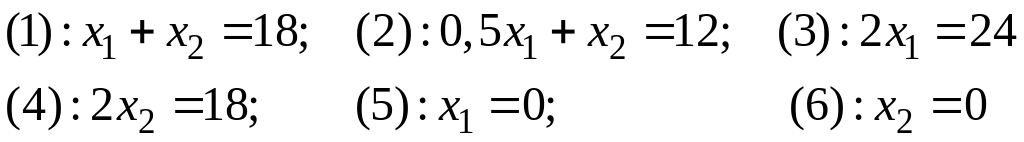 .
.
Область допустимых решений – множество точек многоугольника OABCD.
Строим вектор
![]() и линию уровня
.
Параллельным перемещением прямой
в направлении вектора
находим крайнюю точку
,
в которой целевая функция достигает
максимум. Координаты точки
определяются из решения системы
и линию уровня
.
Параллельным перемещением прямой
в направлении вектора
находим крайнюю точку
,
в которой целевая функция достигает
максимум. Координаты точки
определяются из решения системы
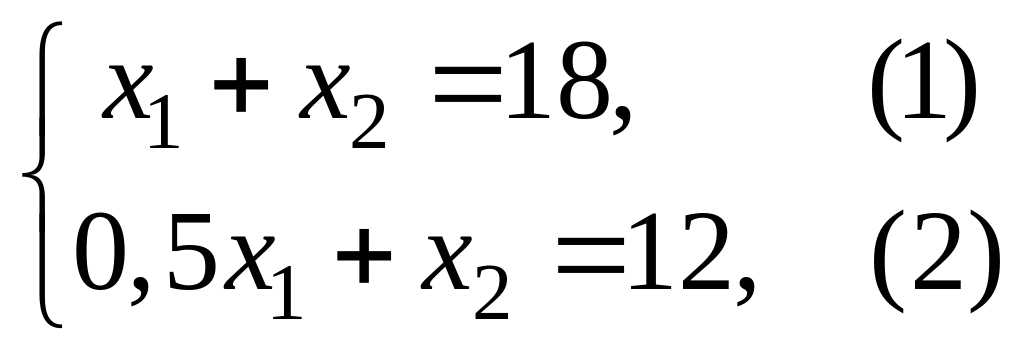 ,
откуда
,
откуда
![]() .
.
Рис. 2.11

Таким образом,
![]() план выпуска
продукции предприятием. Тогда максимальная
прибыль
план выпуска
продукции предприятием. Тогда максимальная
прибыль
![]() (ден. ед.).
(ден. ед.).
Ответ: следует выпускать 12 ед. продукции вида и 6 ед. продукции вида , при этом прибыль составит 840 ден. ед.
Перейдем к геометрической интерпретации ЗЛП с перменными:
; (2.24)
, (2.25)
. (2.26)
Множество планов
![]() ,
компоненты которых удовлетворяют
ограничению равенству
,
геометрически представляет собой
гиперплоскость
-мерного
пространства. Это выпуклое множество.
Множество планов
,
компоненты которых удовлетворяют
неравенству
,
компоненты которых удовлетворяют
ограничению равенству
,
геометрически представляет собой
гиперплоскость
-мерного
пространства. Это выпуклое множество.
Множество планов
,
компоненты которых удовлетворяют
неравенству
![]() ,
образуют полупространство
-мерного
пространства, которое также является
выпуклым множеством.
,
образуют полупространство
-мерного
пространства, которое также является
выпуклым множеством.
Напомним, что выпуклым называется
множество, которое вместе с любыми
своими точками
![]() и
и
![]() содержат и все точки
содержат и все точки
![]() отрезка
отрезка
![]() ,
т.е. точки
,
т.е. точки
![]() ,
где
,
где
![]() ,
являющиеся выпуклыми линейными
комбинациями точек
и
.
Иногда это свойство записывается иначе:
,
являющиеся выпуклыми линейными
комбинациями точек
и
.
Иногда это свойство записывается иначе:
![]() ,
где
,
где
![]() .
.
Множество планов, удовлетворяющих системе ограничений ЗЛП (2.25), (2.26), представляет собой пересечение конечного числа полупространств и потому является выпуклым. Отсюда следует теорема, которую примем без доказательства.
Теорема 2.1. Множество планов ЗЛП выпукло.
Множество планов ЗЛП в практически важных случаях чаще всего представляет собой либо выпуклый многогранник, либо выпуклую многогранную область.
Целевую функцию (2.24) геометрически можно
рассматривать как семейство параллельных
гиперплоскостей
![]() ,
каждой из которых соответствует
определенное значение параметра
.
Вектор
,
каждой из которых соответствует
определенное значение параметра
.
Вектор
![]() ,
перпендикулярный к гиперплоскостям
,
указывает направление наискорейшего
возрастания функции
.
,
перпендикулярный к гиперплоскостям
,
указывает направление наискорейшего
возрастания функции
.
С учетом сказанного задача (2.24) – (2.26)
геометрически сводится к нахождению
точки
![]() многогранника (многоугольной области),
определяемого неравенствами (2.25), (2.26),
через которую проходит гиперплоскость
семейства (2.24), соответствующая наибольшему
значению
.
многогранника (многоугольной области),
определяемого неравенствами (2.25), (2.26),
через которую проходит гиперплоскость
семейства (2.24), соответствующая наибольшему
значению
.
Графическим методом можно решить ЗЛП
с
![]() переменными, если в ее канонической
записи число неизвестных
и число линейно независимых уравнений
связаны соотношением
переменными, если в ее канонической
записи число неизвестных
и число линейно независимых уравнений
связаны соотношением
![]() .
В этом случае каноническую форму задачи
преобразовывают в симметричную, которая
будет содержать не более двух переменных.
Решая эту задачу графически, находят
два компонента оптимального плана.
Подставляя их в ограничения задачи,
определяют и остальные компоненты.
.
В этом случае каноническую форму задачи
преобразовывают в симметричную, которая
будет содержать не более двух переменных.
Решая эту задачу графически, находят
два компонента оптимального плана.
Подставляя их в ограничения задачи,
определяют и остальные компоненты.
Пример 2.7. Найти
![]()
при ограничениях

![]() .
.
Решение. В данной задаче число
неизвестных
![]() ,
а число уравнений в системе ограничений
,
а число уравнений в системе ограничений
![]() .
Так как
.
Так как
![]() ,
то задачу можно решить графически.
,
то задачу можно решить графически.
Решим систему ограничительных уравнений
относительно любых трех неизвестных.
В данном случае проще всего решить
систему относительно
![]() ,
,
![]() и
и
![]() .
Получаем
.
Получаем

![]() .
.
Подставляем выражения для , и в целевую функцию.
![]()
![]() .
.
Из системы ограничений получаем
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
Таким образом, ЗЛП с двумя переменными принимает вид:
![]()
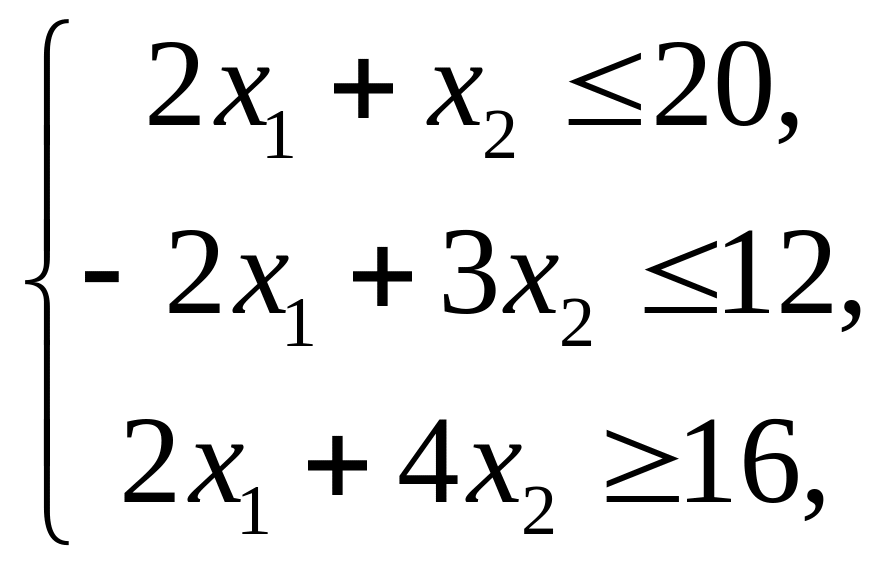
.
Для построения области допустимых решений строим в системе координат соответствующие данным ограничениям-неравенствам граничные прямые, рис. 2.12.:

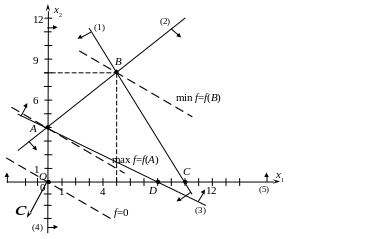
Рис. 2.12
Для нашего примера область допустимых решений – множество точек четырехугольника ABCD, рис 2.12.
Строим вектор
![]()
![]() .
Перпендикулярно вектору
проводим линию уровня f=0.
Параллельным перемещением прямой f=0
находим крайнюю точку
.
Перпендикулярно вектору
проводим линию уровня f=0.
Параллельным перемещением прямой f=0
находим крайнюю точку
![]() ,
в которой целевая функция достигает
максимума, и точку
,
в которой целевая функция достигает
максимума, и точку
![]() ,
в которой целевая функция достигает
минимума.
,
в которой целевая функция достигает
минимума.
Далее подставляем координаты точек
и
в выражения для
,
и
,
и находим остальные координаты
экстремальных точек:
![]() и
и
![]() .
.
При этом
![]() ,
,
![]() .
.
Ответ:
![]() ,
,
![]() .
.
