2.2. Формы записи задач линейного программирования

Модель задачи линейного программирования может быть записана в одной из приведенных ниже форм.

1. Общая, или произвольная, форма записи (ОЗЛП):

,

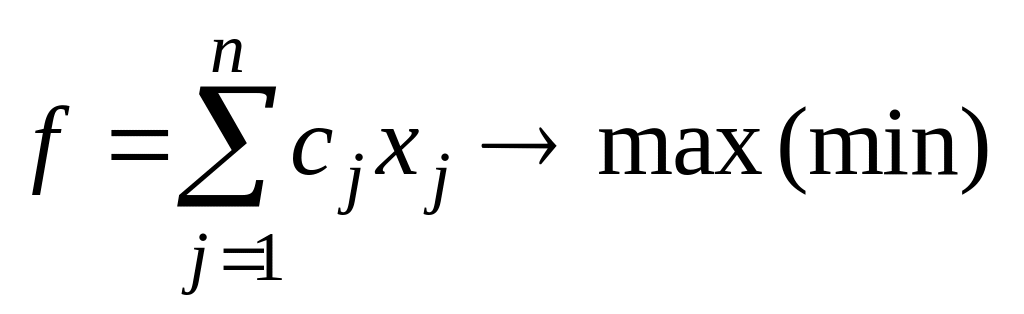при ограничениях:

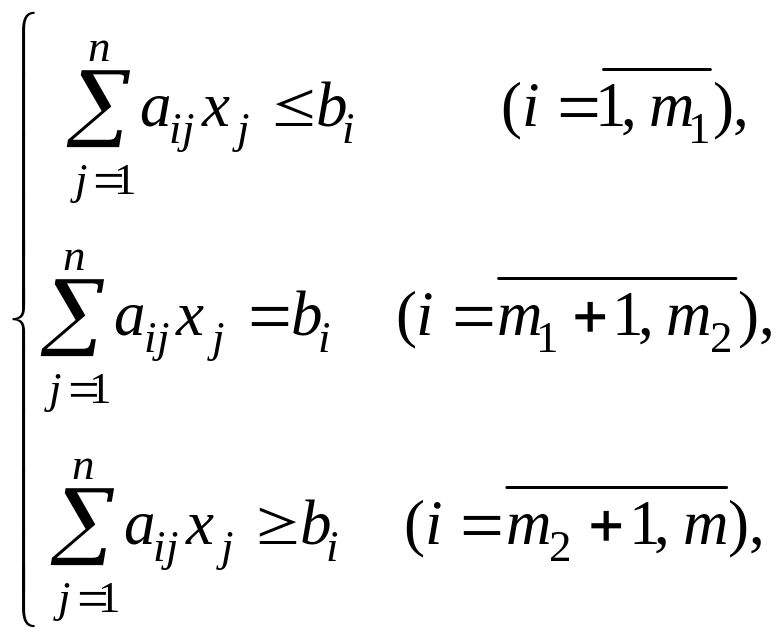
2. Симметричная, или стандартная, форма записи (СФЗЛП):

, ,

, ,

3. Каноническая, или основная, форма записи (КФЗЛП)

,

,

.

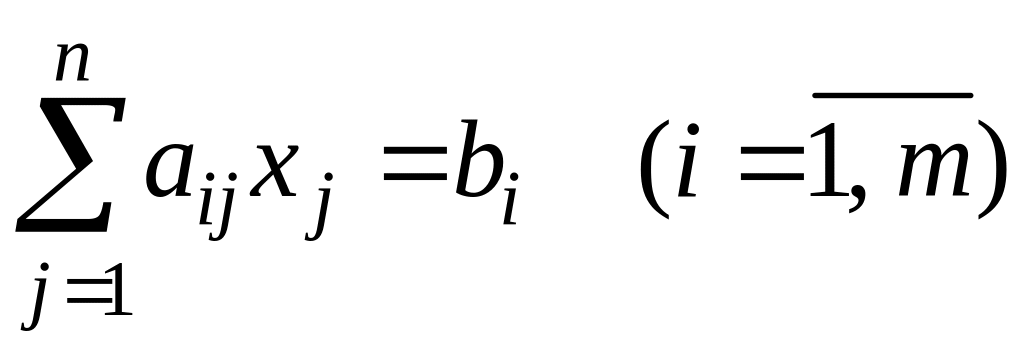Для канонической формы записи ЗЛП иногда используется матричная запись. Введем обозначения:

, , , ,

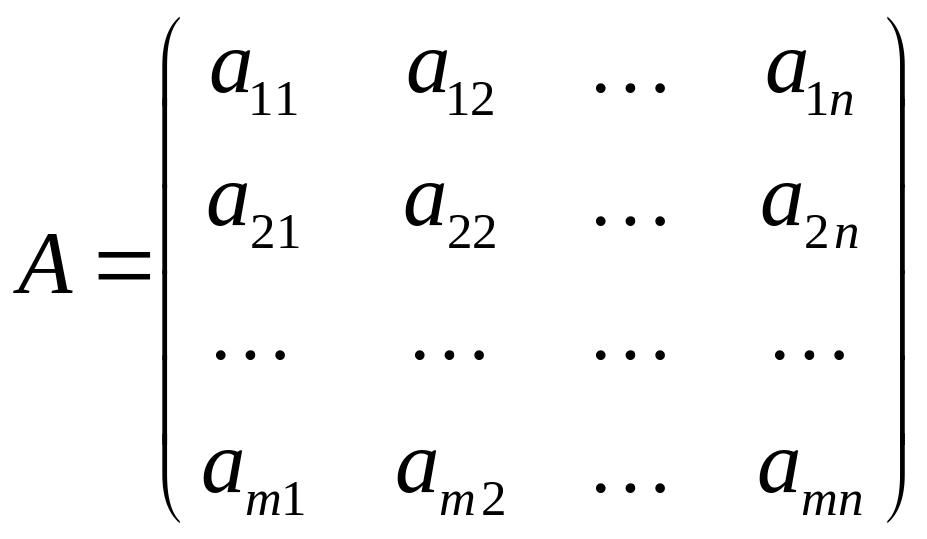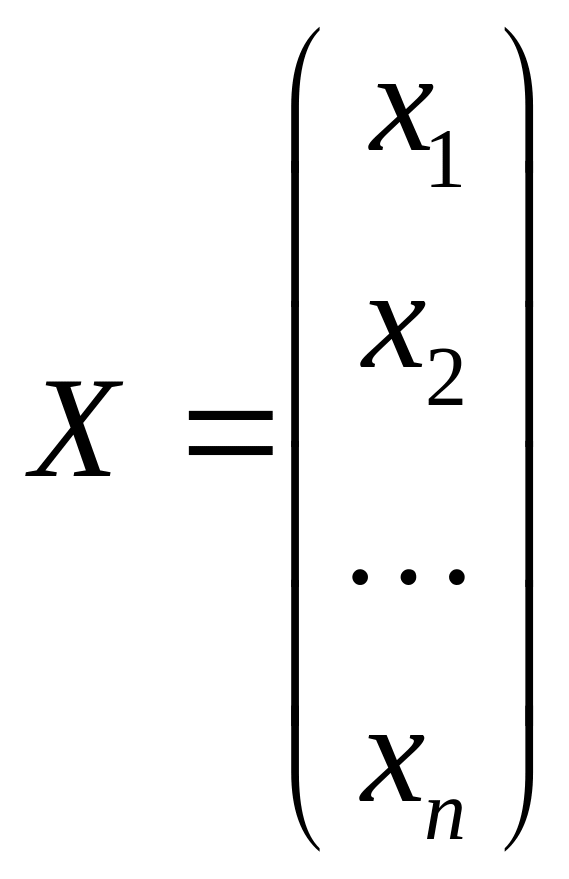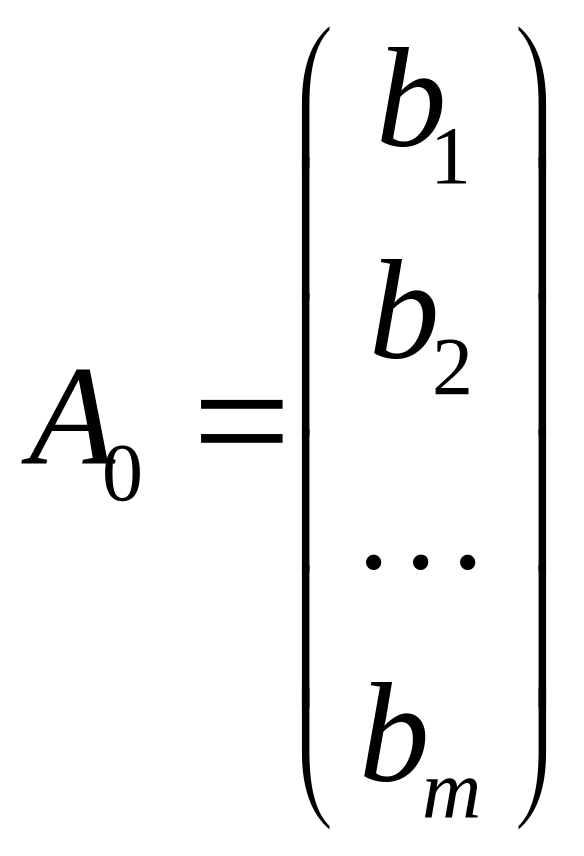где  матрица-строка,  матрица системы уравнений,  матрица-столбец переменных,  матрица-столбец свободных членов.

Тогда каноническая форма задачи примет вид:

;

, ,

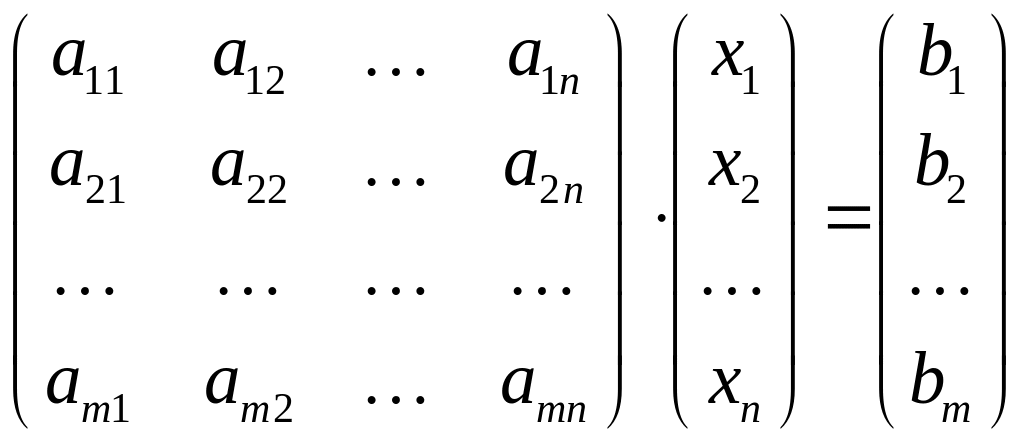или

, .

Полезной является также, векторная форма ЗЛП. Для столбцов матрицы введем обозначения:

, , …, , …, .

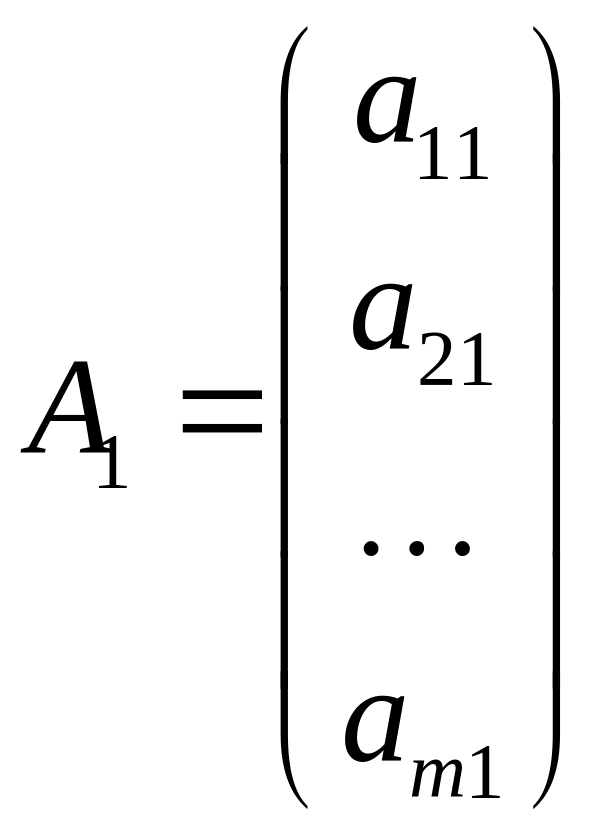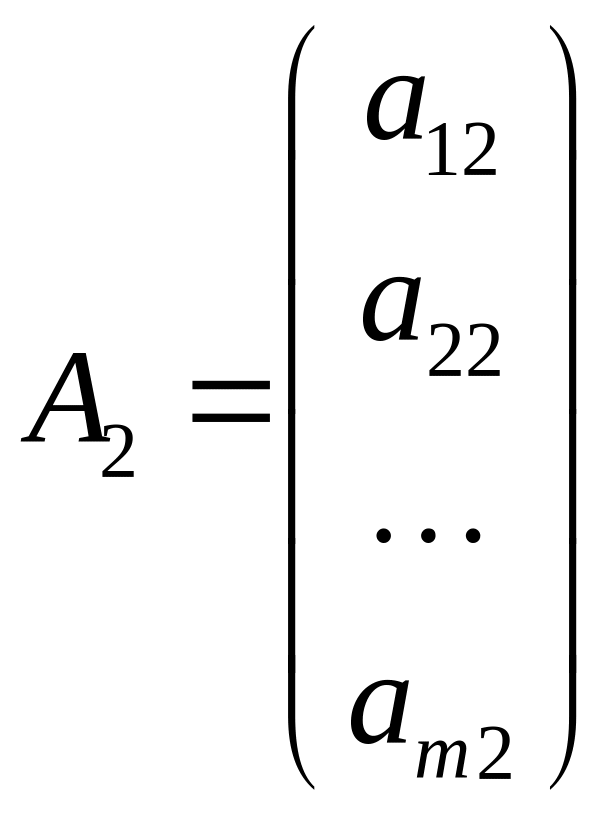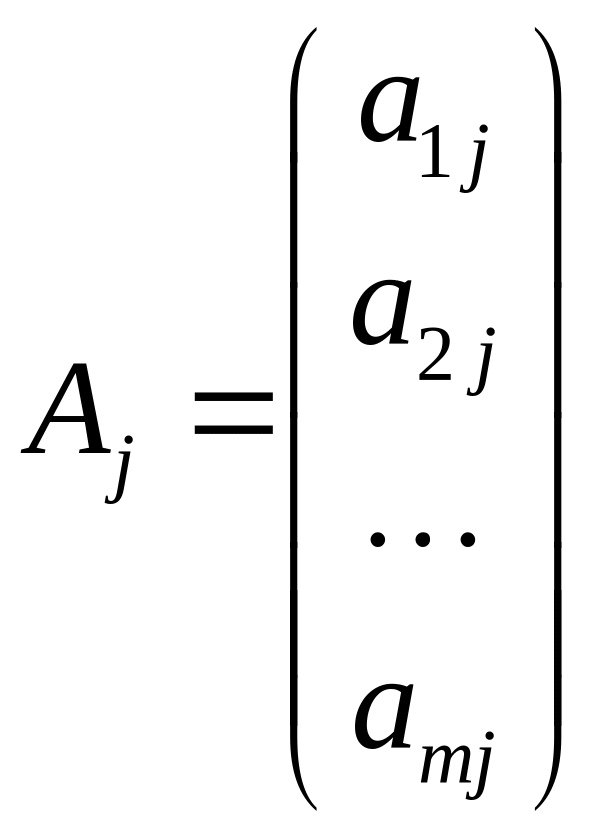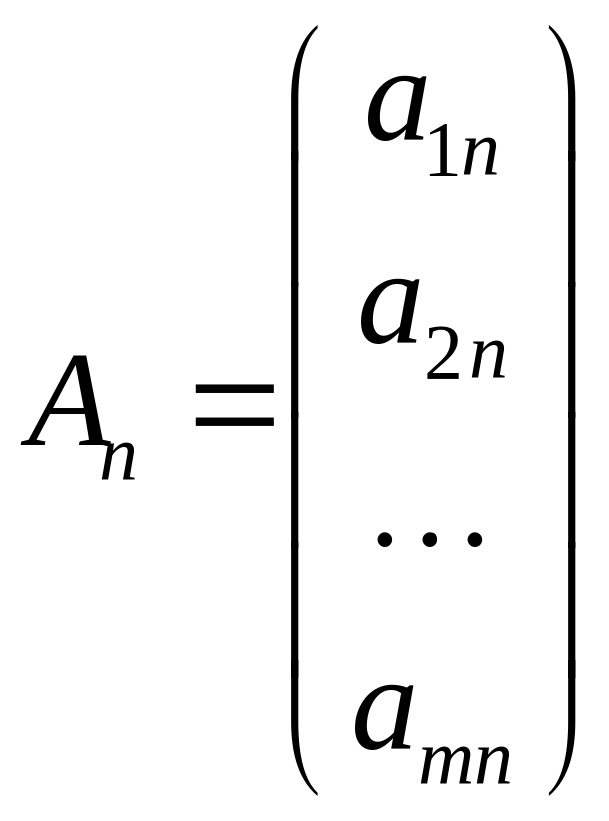Тогда каноническая запись в векторной форме примет вид:

;

, ,

где  скалярное произведение векторов и .

Указанные выше три формы записи ЗЛП эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть сведена к другой форме, т.е. если имеется способ нахождения оптимального решения задачи в одной из указанных форм, то тем самым может быть определен оптимальный план задачи в любой другой форме (говорят о стратегической эквивалентности задачи в любой из форм).

Так при необходимости задачу минимизации можно заменить задачей максимизации, и наоборот. Для функции одной переменной это утверждение очевидно. В самом деле, если – точка минимума функции , то для функции она является точкой максимума, так как графики функций и симметричны относительно оси абсцисс (см. рисунок 2.1).

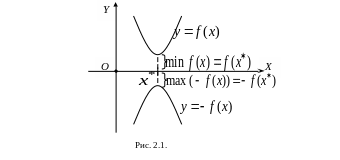
Итак,

.

Данное равенство верно и в случае функции n переменных:

.

Переход к канонической форме

Как следует из примеров задач линейного программирования, в них большинство ограничений задается неравенствами. Наиболее широко используемые методы решения ЗЛП применяются лишь к задачам, записанным в канонической форме. Поэтому приходится переходить от любой формы ЗЛП к ее каноническому виду, причем нужно быть уверенным, что эти формы эквивалентны.

Пусть исходная ЗЛП имеет вид:

; (2.11)

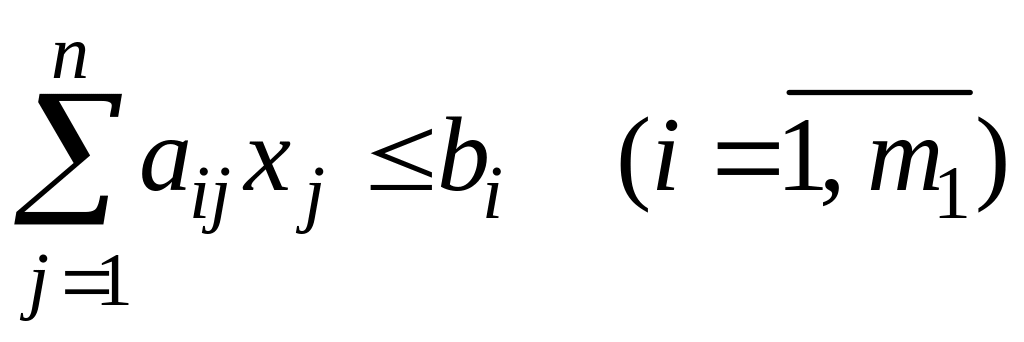, (2.12)

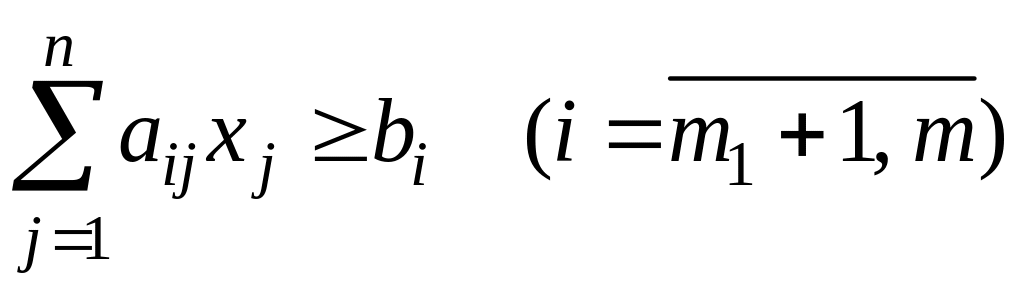, (2.13)

. (2.14)

Преобразуем ее к каноническому виду.

Введем дополнительных (балансовых) неотрицательных переменных . Для того, чтобы неравенства типа « » (2.12) преобразовать в равенства, к их левым частям прибавляем дополнительные переменные , после чего система неравенств (2.12) примет вид:

.

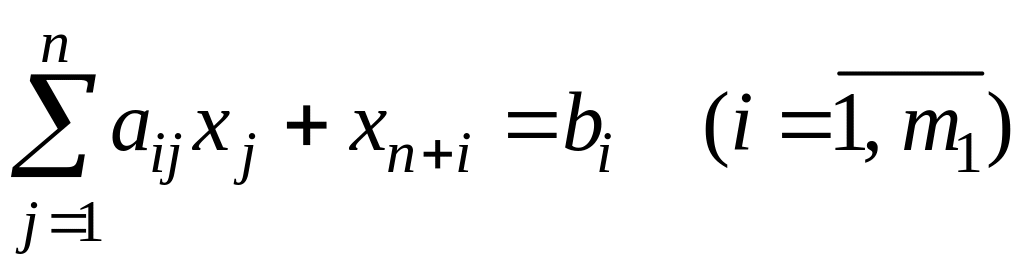Для того, чтобы неравенства типа « » (2.13) преобразовать в равенства, из их левых частей вычитаем дополнительные переменные , после чего система неравенств (2.13) примет вид:

.

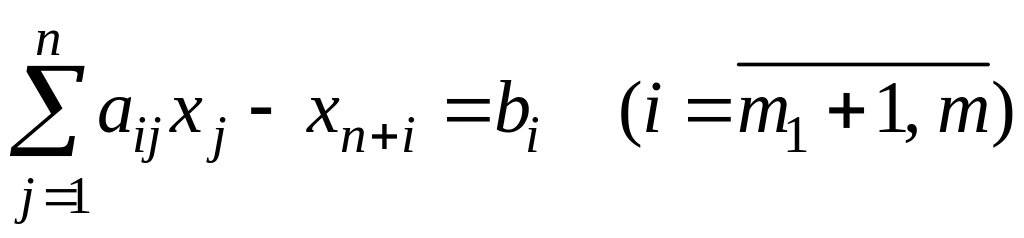Система полученных уравнений с условием неотрицательности дополнительных переменных называют эквивалентной исходной системе неравенств.

Дополнительные переменные в целевую функцию вводятся с коэффициентами, равными нулю. Получаем задачу:

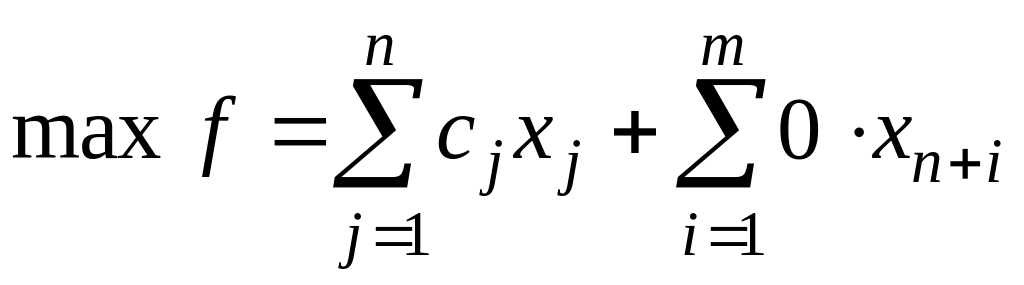; (2.15)

, (2.16)

, (2.17)

, . (2.18)

Задача (2.15)  (2.18) имеет каноническую форму. Задачи (2.11)  (2.14) и (2.15)  (2.18) тесно связаны между собой.

Замечание. Если дана ЗЛП, в которой , то функция заменяется .

Отметим экономический смысл дополнительных переменных. Они в каждой задаче прямо связаны с ее экономическим содержанием.

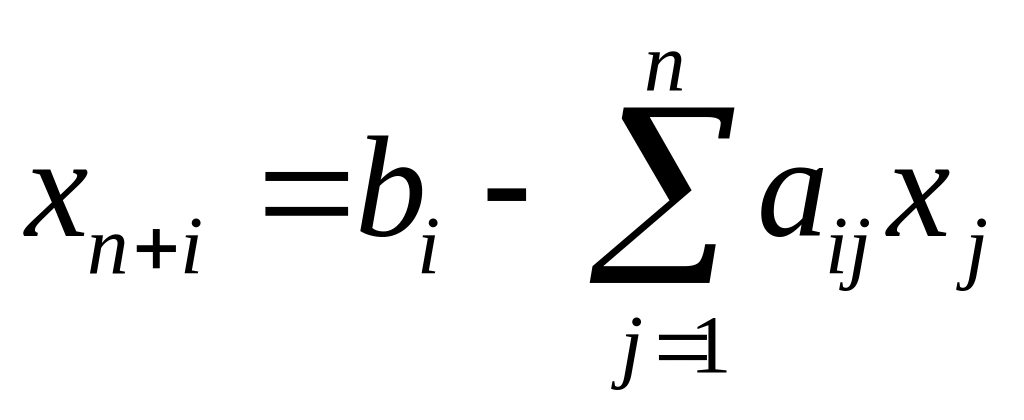
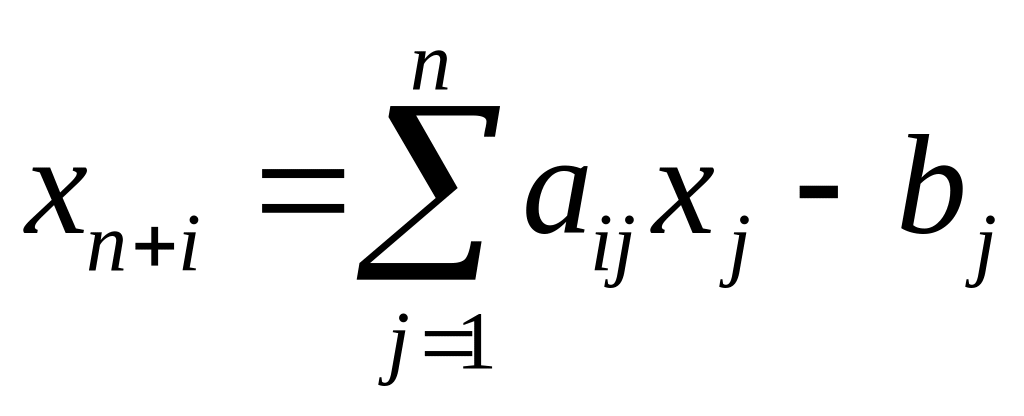Например, для задачи (2.1)  (2.3) о наилучшем использовании ресурсов  дополнительная переменная, которая показывает величину неиспользованного ресурса. Для задачи о смесях (2.8)  (2.10)  дополнительная переменная, которая показывает потребление соответствующего питательного вещества в оптимальном плане сверх нормы.

В ряде производственно-экономических ситуациях не на все переменные налагаются условия неотрицательности. В подобных ситуациях, даже если ограничения представлены в виде равенств, задача не будет канонической. Для представления такой задачи в каноническом виде каждую из переменных , на которые не наложено условие неотрицательности, заменим разностью двух неотрицательных переменных и , т.е. , где , .

Пример 2.3. Привести к канонической форме записи ЗЛП:

.

Решение. Заменим функцию на . Из левых частей ограничений типа «» вычтем неотрицательные переменные , а к левой части ограничения типа «» прибавим неотрицательную переменную . Переменную , которая может быть произвольного знака, заменим разностью двух неотрицательных переменных:

.

В результате получаем модель задачи в каноническом виде:

. 
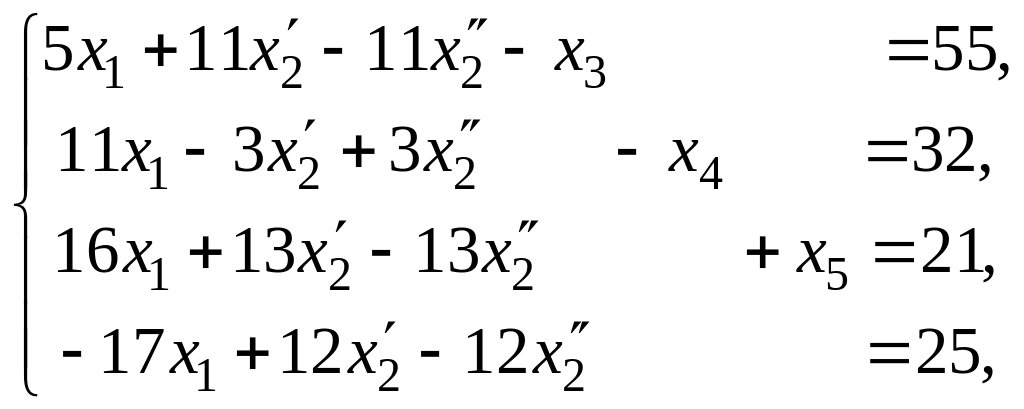
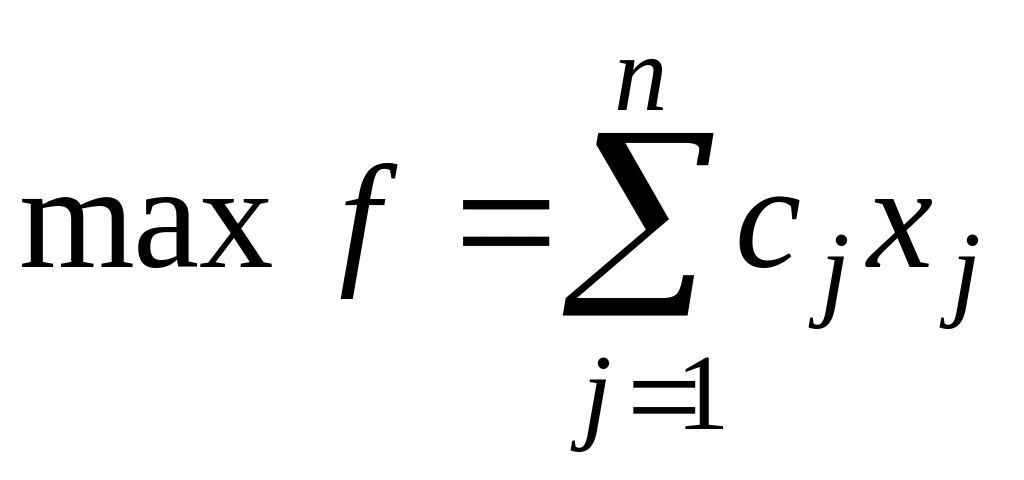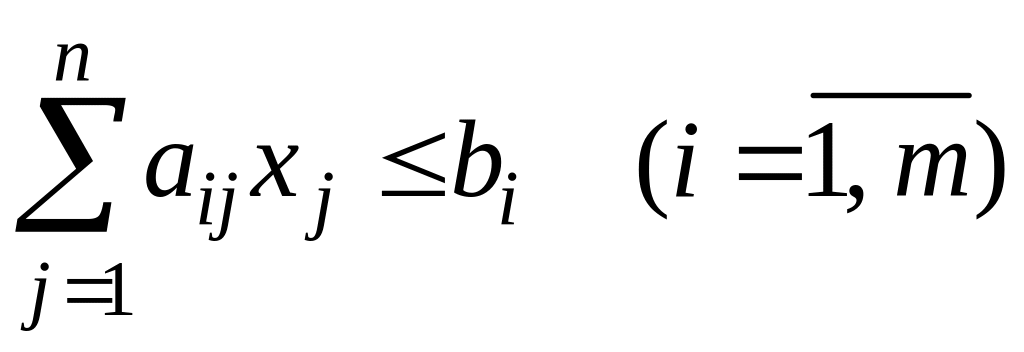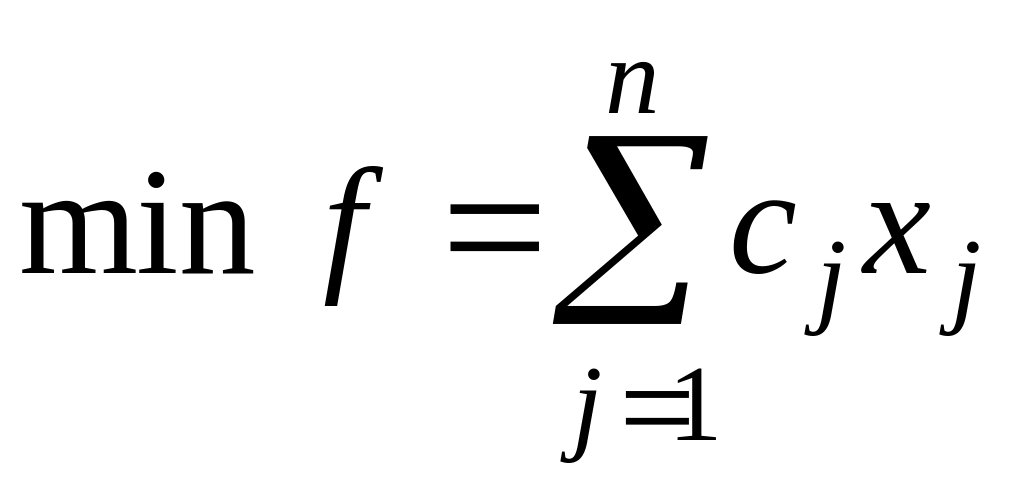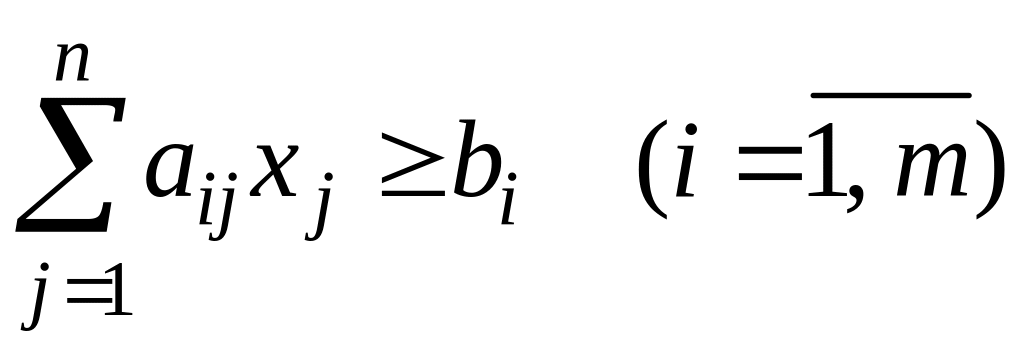