
- •Раздел 1
- •1. Предмет математического программирования
- •1.1. Модель задачи математического программирования
- •1.2. Классификация методов математического программирования
- •2. Линейное программирование
- •2.1. Виды задач линейного программирования
- •Задача о наилучшем использовании ресурсов
- •Задача о раскрое материалов
- •Задача о смесях
- •2.2. Формы записи задач линейного программирования
- •Переход к канонической форме
- •Переход к симметричной форме
- •2.3. Геометрическая интерпретация и графическое решение злп
- •Графический метод решения злп
- •Свойства решений злп
- •Симплексный метод
- •2.5.1. Построение начального опорного плана
- •Нахождение оптимального опорного плана. Переход к нехудшему опорному плану
- •Переход к нехудшему опорному плану
- •3. Двойственность в линейном программировании
- •3.1. Понятие двойственности. Построение двойственных задач
- •Правило построения двойственной задачи
- •Соответствия между неизвестными в паре взаимно двойственных задач
- •Основные теоремы двойственности и их экономическое содержание
Задача о смесях
В различных отраслях производства возникает проблема составления таких рабочих смесей на основе исходных материалов, которые обеспечивали бы получение конечного продукта, обладающего определенными свойствами. К этой группе задач относятся задачи о выборе диеты, составлении кормового рациона в животноводстве, горючих и смазочных смесей, смесей для получения бетона в строительстве и т.д. Высокий уровень затрат на исходные материалы и необходимость повышения эффективности производства выдвигают на первый план следующую задачу: получить продукцию с заданными свойствами при наименьших затратах на исходные сырьевые материалы.
Модель задачи о наилучшем составе смеси рассмотрим на примере задачи о диете.
Имеются пищевые продукты, известные
под номерами
![]() .
Они содержат различные питательные
вещества, обозначаемые номерами
.
Они содержат различные питательные
вещества, обозначаемые номерами
![]() (углеводы, белки, жиры, витамины,
микроэлементы и др.). Единица
-го
продукта содержит
(углеводы, белки, жиры, витамины,
микроэлементы и др.). Единица
-го
продукта содержит
![]() единиц
-го
питательного вещества. Для нормальной
жизнедеятельности в заданный промежуток
времени нужно потреблять не менее
единиц
-го
питательного вещества. Для нормальной
жизнедеятельности в заданный промежуток
времени нужно потреблять не менее
![]() единиц
-го
питательного вещества. Обозначим через
единиц
-го
питательного вещества. Обозначим через
![]() стоимость единицы продукта
-го
вида. Требуется выбрать рацион минимальной
стоимости, содержащий необходимое
количество питательных веществ.
стоимость единицы продукта
-го
вида. Требуется выбрать рацион минимальной
стоимости, содержащий необходимое
количество питательных веществ.
Получаем следующую математическую модель: найти план выпуска количество продуктов каждого вида, обеспечивающих необходимое количество питательных веществ при минимальных затратах на исходные продукты
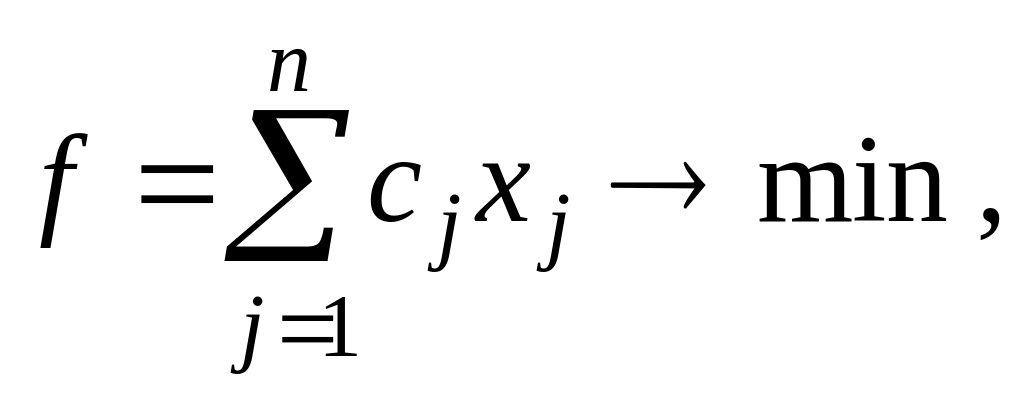 (2.8)
(2.8)
при ограничениях
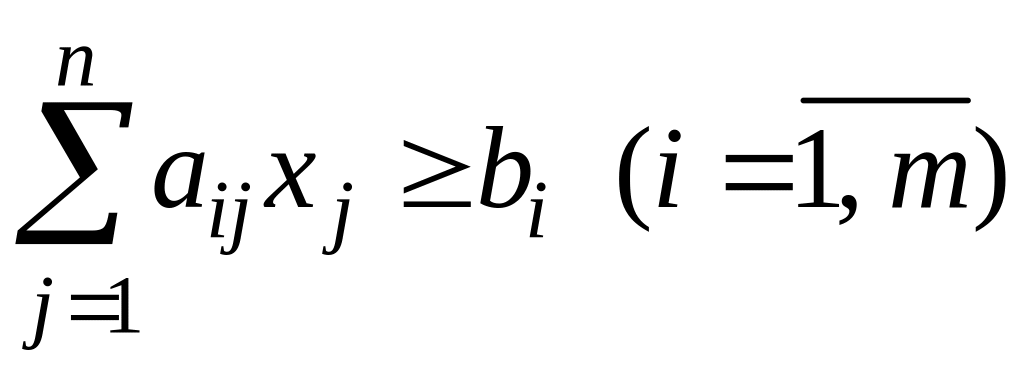 ,
(2.9)
,
(2.9)
и условиях неотрицательности
, (2.10)
где
– вектор цен, т.е. стоимость единицы каждого вида продукта;
количество единиц -го питательного вещества в единице -го вида продукта;
потребность в питательных веществах каждого вида.
К задачам линейного программирования относится также и транспортная задача, формулировка и математическая модель которой будут приведены позже.
Рассмотрим примеры задач линейного программирования.
Пример 2.1. При изготовлении изделий
![]() и
и
![]() используются токарные и фрезерные
станки, а также сталь и цветные металлы.
По технологическим нормам на производство
единицы изделия
требуется 300 и 200 единиц соответственно
токарного и фрезерного оборудования
(в станко-часах), 10 и 20 единиц стали и
цветных металлов (в килограммах). Для
производства единицы изделия
требуется 400, 100, 70 и 50 соответствующих
единиц тех же ресурсов. Цех располагает
12400 и 6800 станко-часов оборудования, 640 и
840 кг материалов. Прибыль от реализации
единицы изделия
составляет 6 тыс. ден. ед.,
– 16 тыс. ден. ед. Требуется:
используются токарные и фрезерные
станки, а также сталь и цветные металлы.
По технологическим нормам на производство
единицы изделия
требуется 300 и 200 единиц соответственно
токарного и фрезерного оборудования
(в станко-часах), 10 и 20 единиц стали и
цветных металлов (в килограммах). Для
производства единицы изделия
требуется 400, 100, 70 и 50 соответствующих
единиц тех же ресурсов. Цех располагает
12400 и 6800 станко-часов оборудования, 640 и
840 кг материалов. Прибыль от реализации
единицы изделия
составляет 6 тыс. ден. ед.,
– 16 тыс. ден. ед. Требуется:
1) свести исходные данные в таблицу, удобную для построения модели;
2) составить математическую модель задачи (показатель эффективности – прибыль).
Решение.
1) Обозначим через
![]() число изделий
,
через
число изделий
,
через
![]() – изделий
,
через
– изделий
,
через
![]() – суммарную прибыль от реализации
производственных изделий. Исходные
данные удобно представить в виде таблицы.
– суммарную прибыль от реализации
производственных изделий. Исходные
данные удобно представить в виде таблицы.
Ресурсы |
Затраты на единицу изделия |
Объем ресурса |
Вид ограничений |
|
|
|
|||
Станки, станко-ч токарные фрезерные Сталь, кг Цветные маталлы, кг |
300 200 10 20 |
400 100 70 50 |
12400 6800 640 840 |
≤ ≤ ≤ ≤ |
Прибыль, тыс. ден. ед. |
6 |
16 |
|
|
План выпуска, шт. |
x1 |
x2 |
|
|
2) Так как каждое изделие
дает прибыль 6 тыс. ден. ед., а таких
изделий изготавливается
ед., то все изделия
дадут прибыль
![]() ;
аналогично изделия
обеспечат прибыль
;
аналогично изделия
обеспечат прибыль
![]() .
Суммарную прибыль можно записать в виде
целевой функции, которая максимизирует
прибыль
.
Суммарную прибыль можно записать в виде
целевой функции, которая максимизирует
прибыль
![]() .
.
Токарного оборудования на выпуск одного
изделия
требуется 300 станко-часов, на изделие
– 400 станко-часов. Тогда для изготовления
изделий
и
изделий
потребуется токарного оборудования
![]() (станко-часов). Так как общий фонд рабочего
времени токарных станков не может
превышать 12400 станко-ч, должно выполняться
неравенство
(станко-часов). Так как общий фонд рабочего
времени токарных станков не может
превышать 12400 станко-ч, должно выполняться
неравенство
![]() .
.
Аналогично можно записать условия, налагаемые на фонд рабочего времени фрезерных станков:
![]() ,
,
и лимитирующие материалы: по стали
![]() ,
,
по цветным металлам
![]() .
.
Итак, искомый план задачи
![]() .
Тогда математическая модель задачи
определяется следующим образом.
.
Тогда математическая модель задачи
определяется следующим образом.
Целевая функция
![]() .
.
Система ограничений
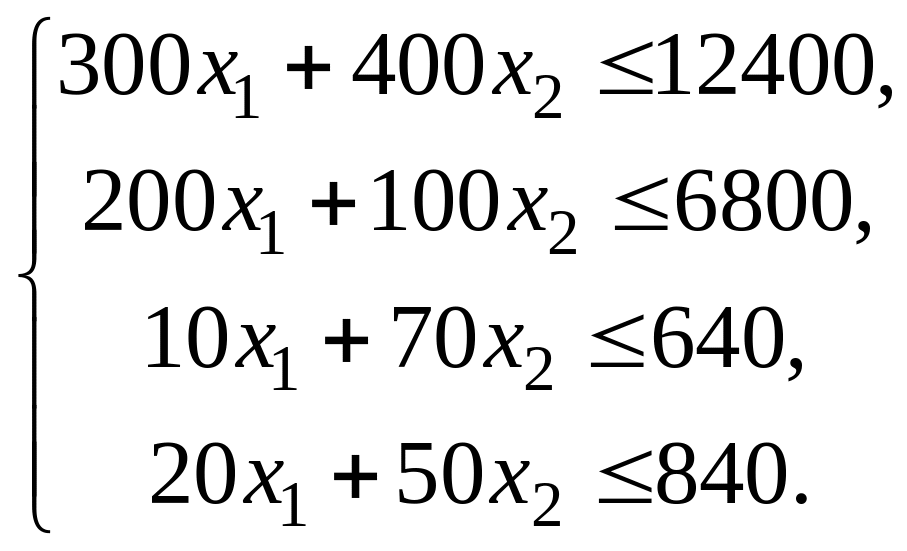
Переменные и не могут быть выражены отрицательными числами, поэтому
![]() .
.
Пример 2.2. На предприятии имеется
листовой материал, представляющий
прямоугольники размера 70110
см2. Требуется выкроить прямоугольные
заготовки типов
![]() ,
число которых соответственно равно
220, 120 и 80. Размеры заготовок следующие:
,
число которых соответственно равно
220, 120 и 80. Размеры заготовок следующие:
![]()
![]()
![]() .
.
Требуется:
1) составить возможные варианты раскроя;
2) построить математическую модель
раскроя материала, минимизирующую
отходы и удовлетворяющую потребность
в заготовках типов
![]() .
.
Решение.
1) Составим хотя бы четыре возможных варианта раскроя листового материала. Заштрихованные места – это отходы, полученные при разрезе листов.
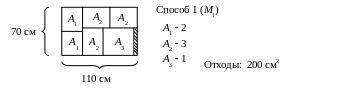
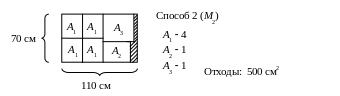
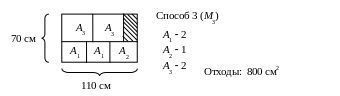
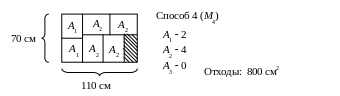
2) Для построения математической модели раскроя листового материала, полученные варианты заносим в таблицу.
Вид заготовки |
Размеры заготовки, см2 |
Способы раскроя |
Потребность в заготовках, шт. |
|||
М1 |
М2 |
М3 |
М4 |
|||
А1 А2 А3 |
3530 3040 4540 |
2 3 1 |
4 1 1 |
2 1 2 |
2 4 0 |
220 120 80 |
Отходы, см2 |
200 |
500 |
800 |
800 |
|
|
Пусть
![]() план задачи, где
план задачи, где
![]() число листов,
раскраиваемых соответствующими способами
число листов,
раскраиваемых соответствующими способами
![]()
![]()
![]() и
и
![]() .
Получаем следующую математическую
модель задачи:
.
Получаем следующую математическую
модель задачи:
![]() ,
,
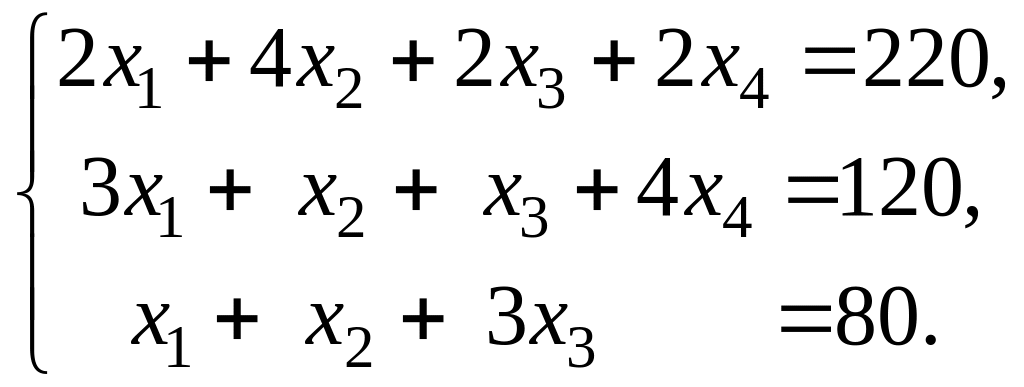
![]()

 f
f