2. Линейное программирование

2.1. Виды задач линейного программирования

Линейное программирование – раздел математического программирования, применяемый при разработке методов отыскания экстремума линейной функции нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования. Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений.

Особенностью ЗЛП является то, что экстремума целевая функция достигает на границе области допустимых решений.

Задача о наилучшем использовании ресурсов

Пусть некоторая производственная единица (цех, завод, объединение и т.д.), исходя из конъюнктуры рынка, технических или технологических возможностей и имеющихся ресурсов, может выпускать n различных видов продукции (товаров), известных под номерами, обозначенными индексом , где каждый j-ый вид продукции обозначим . Предприятие при производстве этих видов продукции должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т.д.). Все виды этих ограничивающих факторов будем называть ресурсами. Пусть их число равно m; поставим с соответствие им индекс . Ресурсы ограничены, и их количества равны соответственно условных единиц. Таким образом, – вектор ресурсов.

Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам производства и т.д. Примем в качестве такой меры, например, цену реализации , т.е. – вектор цен.

Известны также технологические коэффициенты , которые указывают, сколько единиц -го ресурса требуется для производства единицы продукции -го вида. Матрицу коэффициентов называют технологической и обозначают буквой , т.е. .

Обозначим через план выпуска продукции вида , которые обеспечивают предприятию максимум объема реализации при имеющихся объемах ресурсов.

Получаем следующую математическую модель: найти план выпуска продукции видов , обеспечивающий максимум объема реализации в стоимостном выражении

(2.1)

при ограничениях на лимитируемые ресурсы

, (2.2)

и условиях неотрицательности

, (2.3)

где

– вектор цен, т.е. цена реализации единицы каждого вида продукции;

 технологический коэффициент, указывающий, сколько единиц -го ресурса требуется для производства единицы продукции -го вида;

– вектор ресурсов, где -ая компонента вектора соответствует количеству ресурса -го вида.

Аналогичная математическая модель составляется для задачи о выборе оптимальных технологий.

Задача о раскрое материалов

Суть задачи об оптимальном раскрое состоит в разработке таких технологически допустимых планов раскроя, при которых получается необходимый комплект заготовок, а отходы (по длине, площади, объему, массе или стоимости) сводятся к минимуму. Рассмотрим простейшую модель раскроя по одному измерению. Более сложные постановки ведут к задачам целочисленного программирования.

Постановка задачи раскроя по одному измерению длинномерных материалов (прутков, труб, профильного проката и др.) следующая. Пусть имеется штук исходного материала, длина каждого из которых равна . Нужны заготовки видов, длины которых равны . Известна потребность в заготовках каждого вида, которая составляет . Изучение вопроса раскроя (построение технологической карты раскроя) показывает, что можно выделить приемлемых вариантов раскроя исходного материала длиной на заготовки длиной . Обозначим через количество заготовок -го вида, получаемое при раскрое единицы исходного материала по -му варианту,  отходы при раскрое единицы исходного материала по -му варианту.

План задачи , где – количество единиц исходного материала, планируемое к раскрою по -му варианту.

Функция цели – минимум отходов, получаемых при раскрое:

(2.4)

при ограничениях на число единиц исходного материала

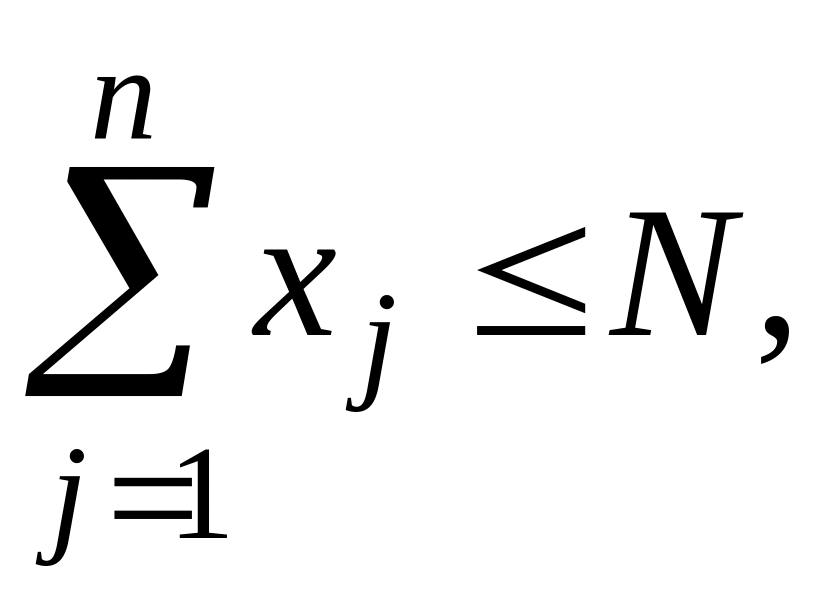(2.5)

на удовлетворение ассортиментного спроса потребителей

(2.6)

и условиях неотрицательности

, (2.7)

где

 отходы при раскрое единицы исходного материала по -му варианту;

 количество заготовок -го вида, получаемое при раскрое единицы исходного материала по -му варианту;

– количество исходного материала, длина каждой из которых равна ;

– потребность в заготовках каждого вида.