Соответствия между неизвестными в паре взаимно двойственных задач
Очевидно, что задача, двойственная двойственной, совпадает с исходной. Поэтому безразлично, какую задачу принять в качестве прямой, а какую – двойственной. Следует говорить о паре взаимно двойственных задач.
Рассмотрим пару двойственных ЗЛП:
Прямая задача |
Двойственная задача |
; , , |
; , , |
Сформулируем несколько теорем (без доказательства).
Теорема 3.1. Для любых допустимых
планов
и
прямой и двойственной ЗЛП справедливо
неравенство
,
т.е.
.
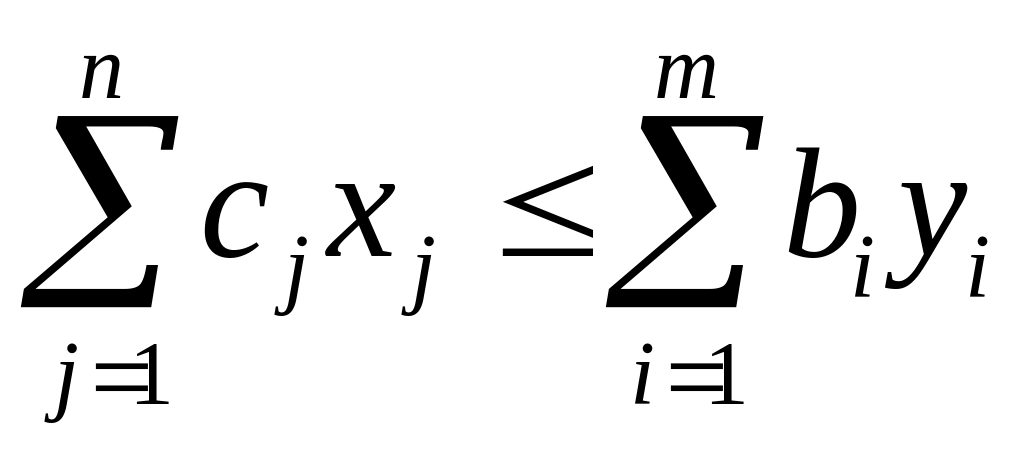Экономическое содержание неравенства
состоит в том, что для любого допустимого
плана производства
и любого допустимого вектора оценок
ресурсов
общая созданная стоимость не превосходит
суммарной оценки ресурсов.
Теорема 3.2 (критерий оптимальности Канторовича).
Если для некоторых допустимых планов
и
пары двойственных задач выполняется
равенство
,
то
и
являются оптимальными планами
соответствующих задач.
Экономическое содержание теоремы 3.2. состоит в том, что план производства и вектор оценок ресурсов являются оптимальными, если цена всей произведенной продукции и суммарные оценки ресурсов совпадают.
Теорема 3.3 (малая теорема двойственности).
Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них.
Как известно, каждую из пары двойственных
задач можно привести к каноническому
виду, путем введения в первую задачу
балансовых неизвестных
,
а во вторую задачу – балансовых переменных
.
Тогда пара двойственных задач примет
вид:
Прямая задача |
Двойственная задача |
;
|
;
|
,
,
,
,Теперь между переменными двойственных задач можно установить соответствие, сопоставляя свободным переменным (СП) одной задачи базисные переменные (БП) другой, и наоборот:
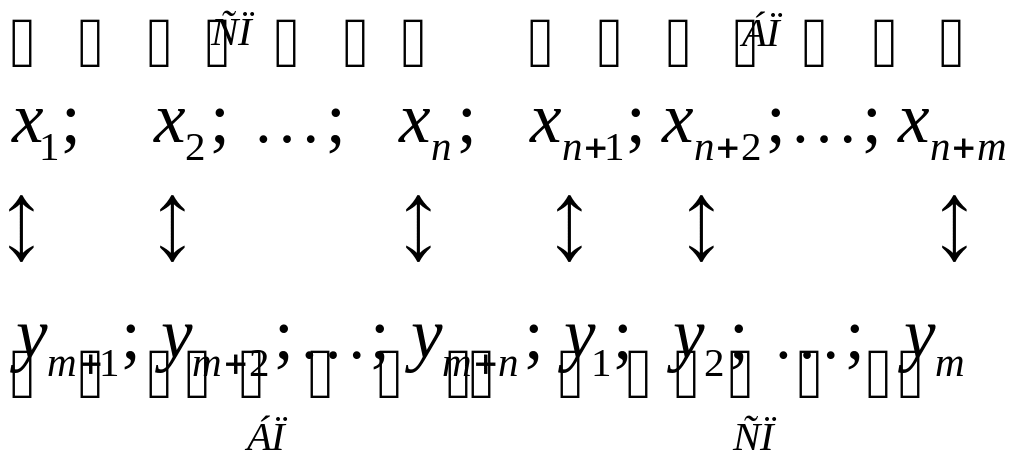(3.7)
Можно выразить базисные переменные в каждой из пары двойственных задач. Получаем
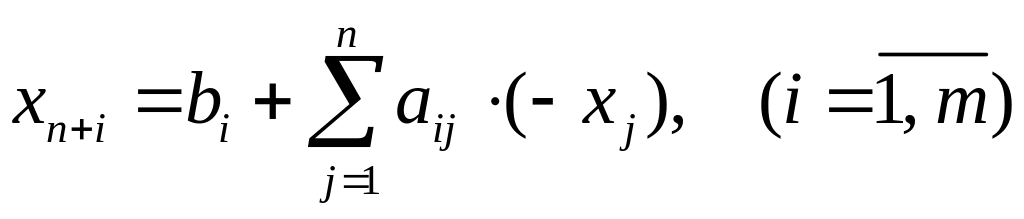
и
.
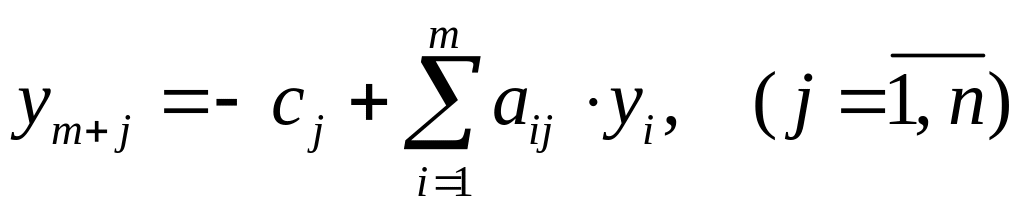Это дает возможность записать данные пары двойственных задач в виде таблиц (табл. 3.1 и 3.2):
Таблица 3.1 Таблица 3.2
и
.
Или же обе таблицы можно записать в виде объединенной таблицы (табл. 3.3):
.
Пример 3.3. Для следующей ЗЛП найти оптимальное решение пары двойственных задач:
;
.
Решение. Прямая задача исходной ЗЛП имеет вид:
;
.
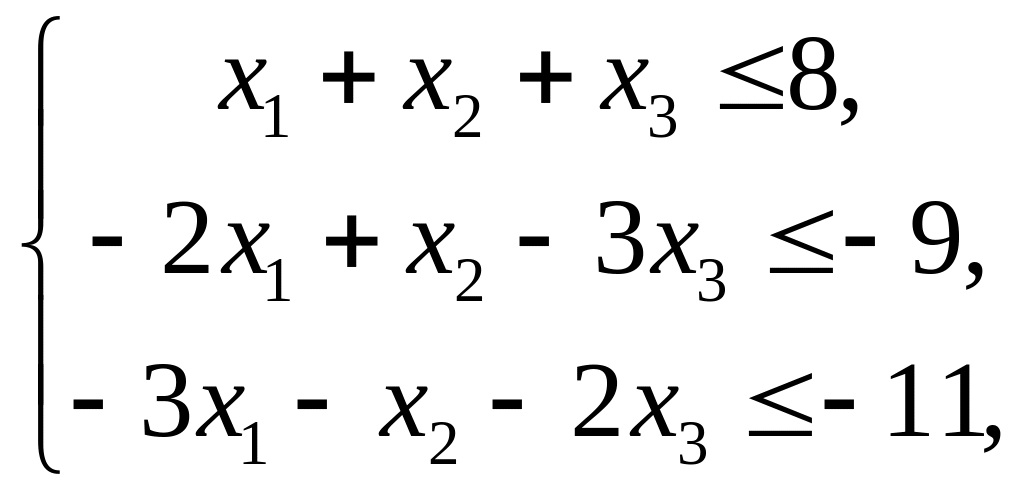
Двойственная задача (см. решение примера 3.1) имеет следующий вид:
;
.
Обе задачи можно привести к каноническому
виду путем введения балансовых переменных
в ограничения прямой задачи и
в ограничения двойственной задачи.
Получаем следующие системы ограничений
каждой пары двойственных задач:
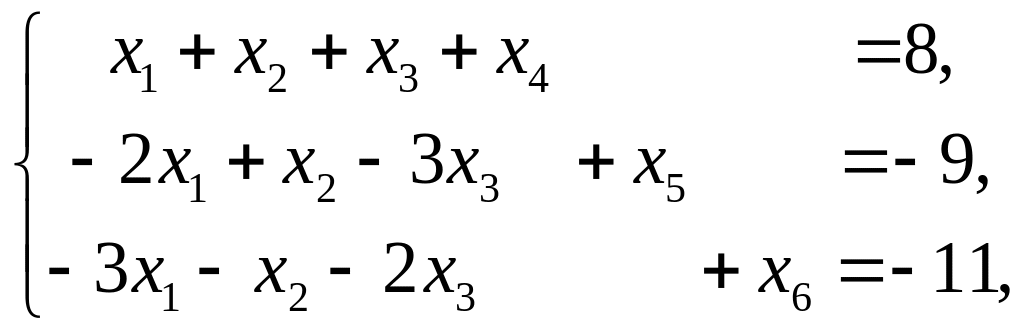
и
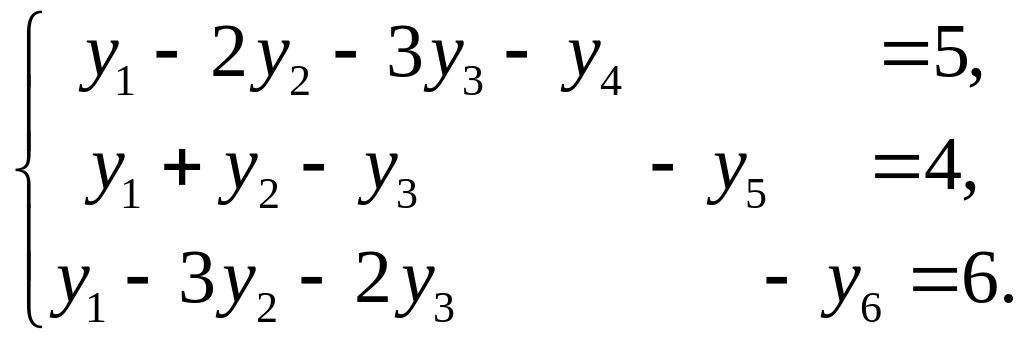
Между переменными можно установить следующее соответствие:
Составляем объединенную симплексную таблицу:
.
За разрешающий элемент берем
,
так как в
-строке
максимальный по модулю отрицательный
элемент
.
Делаем один шаг жордановых исключений.
Получаем следующую симплексную таблицу:
Поскольку в
-строке
все элементы положительные, то получили
следующий единственный оптимальный
план
и
.
Согласно полученному результату
оптимальный план двойственной задачи
и
.
Итак, пара двойственных задач имеет
следующие оптимальные решения:
,
и
.
Ответ: , , .
Замечание. Для решения примера 3.3 можно было бы воспользоваться одной из симплексных таблиц пары двойственных задач (табл. 3.1 или табл. 3.2), а не объединенной симплексной таблицей.
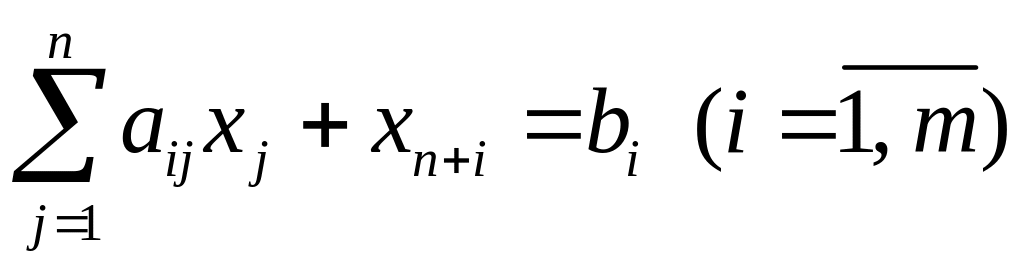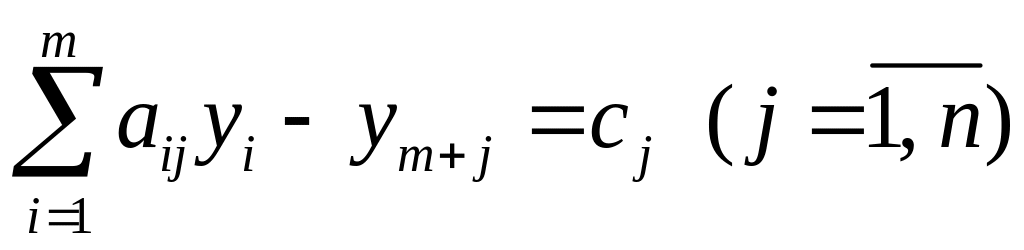