
- •Раздел 1
- •1. Предмет математического программирования
- •1.1. Модель задачи математического программирования
- •1.2. Классификация методов математического программирования
- •2. Линейное программирование
- •2.1. Виды задач линейного программирования
- •Задача о наилучшем использовании ресурсов
- •Задача о раскрое материалов
- •Задача о смесях
- •2.2. Формы записи задач линейного программирования
- •Переход к канонической форме
- •Переход к симметричной форме
- •2.3. Геометрическая интерпретация и графическое решение злп
- •Графический метод решения злп
- •Свойства решений злп
- •Симплексный метод
- •2.5.1. Построение начального опорного плана
- •Нахождение оптимального опорного плана. Переход к нехудшему опорному плану
- •Переход к нехудшему опорному плану
- •3. Двойственность в линейном программировании
- •3.1. Понятие двойственности. Построение двойственных задач
- •Правило построения двойственной задачи
- •Соответствия между неизвестными в паре взаимно двойственных задач
- •Основные теоремы двойственности и их экономическое содержание
3. Двойственность в линейном программировании
3.1. Понятие двойственности. Построение двойственных задач
Понятие двойственности служит иллюстрацией одного из законов диалектики - закона единства и борьбы противоположностей. К аналогичным в математике относятся понятия «плюс» и «минус», «дифференцирование» и «интегрирование», в физике – «положительный» и «отрицательный» заряды, «северный» и «южный» магнитные полюса, в биологии – индивидуумы «мужского» и «женского» вида и т.д.
В линейном программировании понятие
двойственности рассмотрим на примере
задачи оптимального использования
сырья. Пусть на предприятии решили
использовать отходы основного
производства. В плановом периоде
появились отходы сырья
видов в объемах
единиц (![]() ).
Из этих отходов, учитывая специализацию
предприятия, можно наладить выпуск
видов неосновной продукции. Обозначим
через
норму расхода сырья
-го
вида на единицу
-й
(
).
Из этих отходов, учитывая специализацию
предприятия, можно наладить выпуск
видов неосновной продукции. Обозначим
через
норму расхода сырья
-го
вида на единицу
-й
(![]() )
продукции,
цена реализации
единицы
-й
продукции (реализация обеспечена).
Неизвестные величины задачи:
объемы выпуска
-й
продукции, обеспечивающие предприятию
максимум выручки.
)
продукции,
цена реализации
единицы
-й
продукции (реализация обеспечена).
Неизвестные величины задачи:
объемы выпуска
-й
продукции, обеспечивающие предприятию
максимум выручки.
Математическая модель задачи:
![]() ;
(3.1)
;
(3.1)
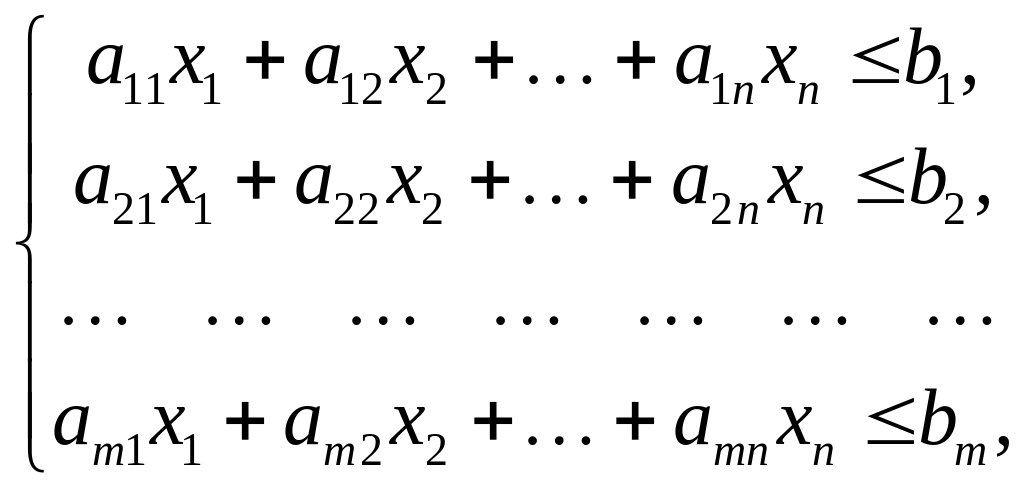 (3.2)
(3.2)
![]() .
(3.3)
.
(3.3)
Предположим далее, что с самого начала
при изучении вопроса об использовании
отходов основного производства на
предприятии появилась возможность
реализации их некоторой организации.
Необходимо установить прикидочные
оценки (цены) на эти отходы. Обозначим
их
![]() .
Оценки должны быть установлены исходя
из следующих требований, отражающих
несовпадающие интересы предприятия и
организации:
.
Оценки должны быть установлены исходя
из следующих требований, отражающих
несовпадающие интересы предприятия и
организации:
общую стоимость отходов сырья покупающая организация стремится минимизировать;
предприятие согласно уступить отходы только по таким ценам, при которых оно получит за них выручку, не меньшую той, что могло бы получить, организовав собственное производство.
Эти требования формализуются в виде следующей ЗЛП.
Требование 1 покупающей организации – минимизировать покупки:
![]() ;
(3.4)
;
(3.4)
Требование 2 предприятия, реализующего отходы сырья, можно сформулировать в виде системы организаций. Предприятие откажется от выпуска каждой единицы продукции первого вида, если
![]()
где левая часть означает выручку за сырье, идущее на единицу продукции первого вида, правая – ее цену.
Аналогичные рассуждения легко провести в отношении выпуска продукции каждого вида. Поэтому требование предприятия, реализующего отходы сырья, можно формализовать в виде следующей системы ограничений:
 (3.5)
(3.5)
По смыслу задачи оценки должны быть неотрицательными:
![]() .
(3.6)
.
(3.6)
Переменные
![]() называются двойственными оценками
или объективно обусловленными
оценками. В зарубежной литературе
их называют теневыми ценами.
называются двойственными оценками
или объективно обусловленными
оценками. В зарубежной литературе
их называют теневыми ценами.
Задачи (3.1) (3.3) и (3.4) (3.6) называются парой взаимно двойственных ЗЛП. Так как задачи (3.1) (3.3) и (3.4) (3.6) записаны в симметричной форме, их принято называть парой симметричных двойственных задач.
Пара взаимно двойственных симметричных задач в виде коечных сумм имеет вид:
Прямая задача |
Двойственная задача |
, |
|
или в матричной форме:
Прямая задача |
Двойственная задача |
, |
|
Можно показать, что если в качестве прямой принять задачу (3.4) (3.6) об определении оптимальных оценок сырья, то двойственной к ней будет задача (3.1) (3.3) об определении оптимального плана выпуска продукции.
Из моделей (3.1) (3.3) и (3.4) (3.6) непосредственно видно, что, имея математическую модель одной из этих задач, можно легко построить модель двойственной к ней задачи.
Сопоставляя модели (3.1) (3.3) и (3.4) (3.6), можно сформулировать правило построения двойственной задачи.

 ;
; ,
,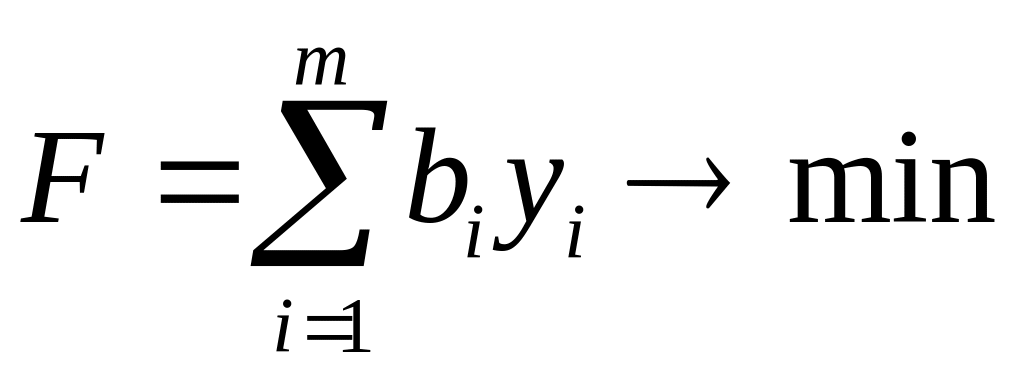 ;
; ,
,