.5. Биномиальный закон распределения случайной величины
Случайная
величина
дискретного типа называется распределенной
по биномиальному закону, если ее возможные
значения
,
а вероятность того, что
определяется формулой Бернулли
,
(
.15)
где
.
Биномиальное
распределение реализуется, когда
случайная величина
выражает
число появлений некоторого события
при
независимых
испытаниях с двумя исходами:
.
Вероятность появления события
постоянна и равна
.
Математическое ожидание и дисперсия случайной величины, распределенной по биномиальному закону, равны соответственно
.
(
.16)
.6. Нормальный закон распределения случайной величины
Случайная
величина
называется распределенной по нормальному
закону с параметрами
,
коротко:
если плотность распределения вероятности
имеет вид:
(
.17)
Математическое
ожидание и дисперсия совпадают с
параметрами нормального закона
распределения:
–
среднее квадратичное отклонение.
Функция распределения случайной величины :
(
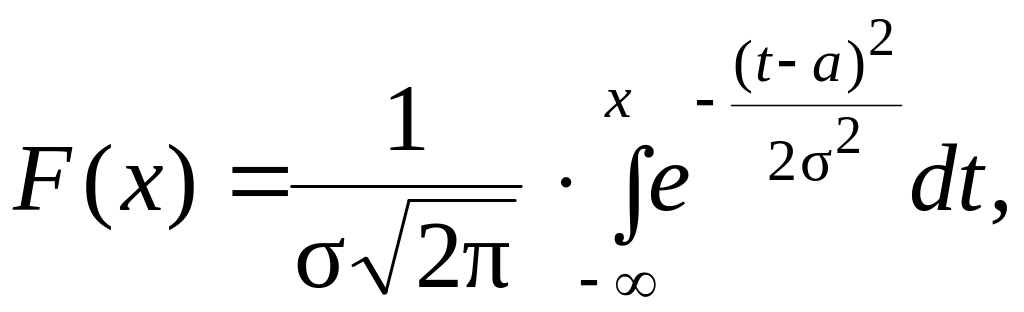.18)
или
где
– интегральная функция Лапласа.
Используем
связь функции
со стандартной функцией Лапласа
:
.
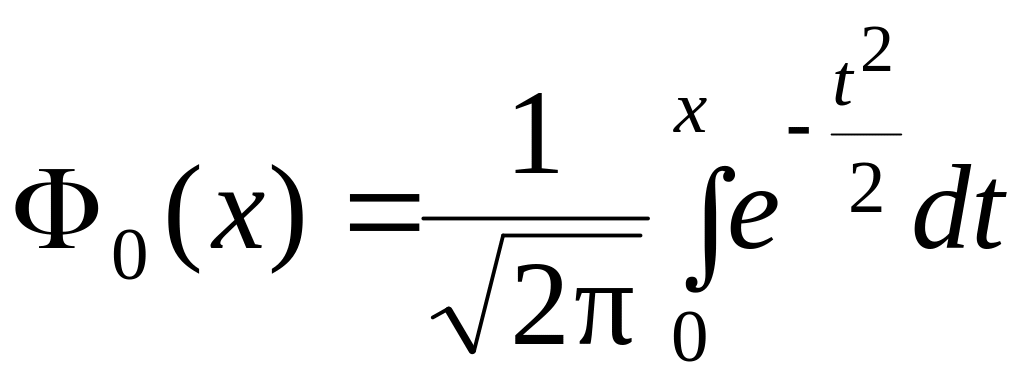Функция
распределения
примет вид:
.
Для вероятностей попадания в заданный интервал получим выражения:
;
(
.19)
(
.20)
(
.21)
Для вероятности попадания в симметричный относительно математического ожидания интервал справедлива формула:
(
.22)
.7. Примеры расчета
Задача
.1.
Случайная
величина
задана таблицей распределения. Найти
вероятность
,
интегральную функцию распределения
,
математическое ожидание
,
дисперсию
,
среднее квадратичное отклонение
и
вероятность события:
.
Построить график функции распределения
.
Таблица 2
-
0
1
2
4
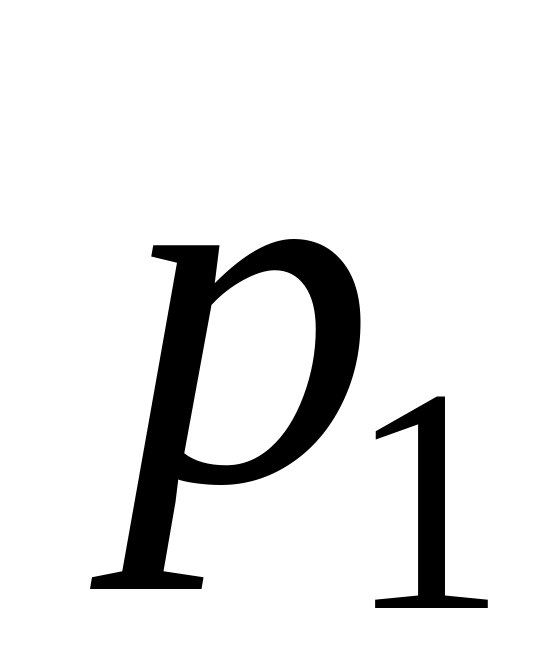
0,14
0,46
0,28
Решение.
Так как +0,14+0,46+0,28=1, то =1- 0,14- 0,46- 0,28=0,12.
Функцию распределения дискретной случайной величины найдем по формуле ( .3):
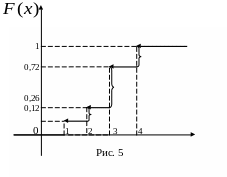
График функции распределения случайной величины представлен на рис.5.
Вероятность попадания в интервал находим по формуле ( .2):
Математическое ожидание, дисперсию дискретной случайной величины находим по формулам (2.8) и (2.9):
Среднее
квадратичное отклонение
Ответ:
рис.5;
Задача
.2.
В коробке 10 деталей, из них 3 нестандартных.
Для проверки наудачу извлечены 3 детали.
Найти ряд распределения случайной
величины
– число нестандартных деталей в
контрольной партии, функцию распределения
случайной
величины
вероятность
события
.