Задача о "расшивке узких мест производства"

При выполнении оптимальной производственной программы второй и третий ресурсы используются полностью, т.е. образуют узкие места производства. Будем их заказывать дополнительно. Пусть T (t₁, t₂, t₃) – вектор дополнительных объемов ресурсов. Так как мы будем использовать найденные двойственные оценки ресурсов, то должно выполняться условие:

H + Q ^-1T 0.

Задача состоит в том, чтобы найти вектор T (0, t₂, t₃), максимизирующий суммарный прирост прибыли

W = 8t₂ + 2t₃ (1)

при условии сохранения двойственных оценок ресурсов (и, следовательно, структуры производственной программы)

(2)

предполагая, что можно надеяться получить дополнительно не более 1/3 первоначального объема ресурса каждого вида

t ₁ 316

0 <=1/3* 216 (3)

t₃ 199

По смыслу задачи t₁  0, t₃  0

2 8 + 1/28*t₁  0

7 - 4/7*t₁ - 1/7*t₃  0

23 –3/28*t₁ + 2/7 t₃  0

t₁  316/3

t₃  199/3

t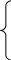 ₁  -784

4/7*t₁ + 1/7*t₃  7

–3/28*t₁ + 2/7 t₃  23

t₁  316/3

t₃  199/3

t₁  0, t₃ 0

y₃

Grad W = (4;3)

A(0;49)

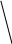
y₁

Находим координаты точки А(t1,t2). t₁ = 0, t₂ =49, и прирост прибыли составляет 0*4+49*3=147 рублей.

cj	31	14	25	50	b	x4+i	yi	ti
aij	4	0	8	7	316	0	-3/28	0
	3	2	5	1	216	7	0	49
	5	6	3	7	199	0	2/7	0
xj	23	0	28	0	1861			147
j	0	8	0	20

3. Транспортная задача линейного программирования

Транспортная задача формулируется следующим образом. Однородный продукт, сосредоточенный в m пунктах производства (хранения) в количествах а₁, а₂, ... а_m единиц, необходимо распределить между n пунктами потребления, которым необходимо соответственно b₁, b₂, ... b_n единиц. Стоимость перевозки единицы продукта из i-го пункта отправления в j-ый пункт назначения равна с_ij и известна для всех маршрутов. Необходимо составить план перевозок, при котором запросы всех пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах производства и общие транспортные расходы по доставке продуктов были минимальными.

Для решения транспортной задачи чаще всего применяется метод потенциалов.

Пусть исходные данные задачи имеют вид:

2 3 4 1

А(40, 60, 70) В (36; 32; 40; 53); С = 4 2 1 2

2 7 7 1

Общий объем производства а _i = 40+60+70 = 170; требуется всем потребителям b_i = 36+32+40+53 = 161, т.е. имеем открытую модель транспортной задачи. Для превращения ее в закрытую вводим фиктивный пункт потребления с объемом потребления 170-161 = 9 единиц, причем тарифы на перевозку в этот пункт условимся считать равными нулю, помня, что переменные, добавляемые к левым частям неравенств для превращения их в уравнения, входят в функцию цели с нулевыми коэффициентами.

Первое базисное допустимое решение легко построить по правилу северо-западного угла.

Потребление	b1 = 36	b2 = 32	b3 = 40	b4 = 53	b5 = 9
Производство
а1 = 40	36	4			*	p1 =0
a2 = 60		28	32			p2
a3 = 70			8	53	9	p3
	q1	q2	q3	q4	q5

Следует иметь в виду, что по любой транспортной таблице можно восстановить соответствующий предпочитаемый эквивалент системы уравнений, в таблице записаны лишь правые части уравнений, причем номер клетки показывает, какая неизвестная в соответствующем уравнении является базисной. В любой транспортной таблице должно быть m + n - 1 занятых клеток.

Обозначим через  ) вектор симплексных множителей или потенциалов. Тогда _ij = A_ij - с_ij

i = 1,m; j = 1,n

откуда следует

 _ij = p_i + q_j - c_ij i = 1,m; j = 1,n

Один из потенциалов можно выбрать произвольно. Положим, что р₁ = 0. Остальные потенциалы находим из условия, что для базисных клеток . В данном случае получаем

₁₁ = 0, p₁ + q₁ - c₁₁ = 0, 0 + q₁ - 2 = 0, q₁ = 2

₁₂ = 0, p₁ + q₂ - c₁₂ = 0, 0 + q₂ -3 = 0, q₂ = 3

₂₂ = 0, p₂ + q₂ - c₂₂ = 0, р₂ +3 - 2 = 0, р₂ = 1

₂₃ = 0, p₂ + q₃ – c₂₃ = 0, 1 + q₃ - 1 = 0, q₃ = 0

₃₃ = 0, p₃ + q₃ – c₃₃ = 0, р₃ + 0 - 7 = 0, p₃ = 7

₃₄ = 0, p₃ + q₄ – c₃₄ = 0, 7 + q₄ - 1 = 0, q₄ = 6

₃₅ = 0, p₃ + q₅ – c₃₅ = 0, 7 + q₅ - 0 = 0, q₅ = -7

З атем по формуле

_ij = p_i + q_j - c_ij i = 1, m; j = 1, n

вычисляем оценки всех свободных клеток:

₂₁ = p₂ + q₁ - c₂₁ = 1 + 2 - 2 = 1

₃₁ = p₃ + q₁ - c₃₁ = 7 + 2 - 2 = 7

₃₂ = p₃ + q₂ - c₃₂ = 7 + 3 - 7 = 3

₁₃ = p₁ + q₃ – c₁₃ = 0 + 0 - 4 = -4

₁₄ = p₁ + q₄ – c₁₄ = 0 + 6 - 1 = 5

₂₄ = p₂ + q₄ – c₂₄ = 1 + 6 - 2 = 5

₁₅ = p₁ + q₅ – c₁₅ = 0 - 7 - 0 = -7

₂₅ = p₂ + q₅ – c₂₅ = 1 - 7 - 0 = -6

Находим наибольшую положительную оценку

max ( ) = 7 =_

Для найденной свободной клетки 31 строим цикл пересчета - замкнутую ломаную линию, соседние звенья которой взаимно перпендикулярны, сами звенья параллельны строкам и столбцам таблицы, одна из вершин находится в данной свободной клетке, а все остальные - в занятых клетках. Это будет 31-11-12-22-23-33. Производим перераспределение поставок вдоль цикла пересчета

36	4			36-	4+			28	12
	28	32			8-	32+			20	40
		8				8-		8

_MAX = 8

Получаем второе базисное допустимое решение:

Потребление	b1 = 36	b2 = 32	b3 = 40	b4 = 53	b5 = 9
Производство
а1 = 40	28	12			*	p1 =0
a2 = 60		20	40			p2
a3 = 70	8			53	9	p3
	q1	q2	q3	q4	q5

Находим новые потенциалы, новые оценки.

₁₁ = 0, p₁ + q₁ – c₁₁ = 0, 0 + q₁ – 2 = 0, q₁ = 2

₁₂ = 0, p₁ + q₂ – c₁₂ = 0, 0 + q₂ – 3 = 0, q₂ = 3

₂₂ = 0, p₂ + q₂ – c₂₂ = 0, р₂ + 3 – 2 = 0, р₂ = 1

₂₃ = 0, p₂ + q₃ – c₂₃ = 0, 1 + q₃ – 1= 0, q₃ = 0

₃₃ = 0, p₃ + q₃ – c₃₃ = 0, р₃ + 0 – 7 = 0, p₃ = 7

₃₄ = 0, p₃ + q₄ – c₃₄ = 0, 7 + q₄ - 1 = 0, q₄ =-6

₁₅ = 0, p₁ + q₅ – c₁₅ = 0, 0 + q₅ - 0 = 0, q₅ = 0

₂₁ = p₂ + q₁ - c₂₁ = 1 + 2 – 4 = -1

₃₁ = p₃ + q₁ - c₃₁ = 7 + 2 – 2 = 7

₃₂ = p₃ + q₂ - c₃₂ = 7 + 3 – 7 = 3

₁₃ = p₁ + q₃ – c₁₃ = 0 + 0 – 4 = -4

₁₄ = p₁ + q₄ – c₁₄ = 0 - 6 – 1 = -7

₂₄ = p₂ + q₄ – c₂₄ = 1 - 6 – 2 = -7

₂₅ = p₂ + q₅ – c₂₅ = 1 + 0 – 0 = 1

₃₅ = p₃ + q₅ – c₃₅ = 7 + 0 – 0 = 7

Находим наибольшую положительную оценку

max ( ) = 7 =_

Для найденной свободной клетки 31 строим цикл пересчета 11-31-14-34. Производим перераспределение поставок вдоль цикла пересчета

28			28-				28
8	53		8+	53-		36	25

_MAX = 28

Потребление	b1 = 36	b2 = 32	b3 = 40	b4 = 53	b5 = 9
Производство
а1 = 40		12		28	*	p1 =0
a2 = 60		20	40			p2
a3 = 70	36			25	9	p3
	q1	q2	q3	q4	q5

Находим новые потенциалы, новые оценки.

₁₁ = 0, p₁ + q₁ – c₁₁ = 0, 0 + q₁ – 2 = 0, q₁ = 2

₁₂ = 0, p₁ + q₂ – c₁₂ = 0, 0 + q₂ – 3 = 0, q₂ = 3

₂₂ = 0, p₂ + q₂ – c₂₂ = 0, р₂ + 3 – 2 = 0, р₂ = 1

₂₄ = 0, p₂ + q₄ – c₂₄ = 0, 1 + q₄ – 2 = 0, q₄ = 1

₃₄ = 0, p₃ + q₄ – c₃₄ = 0, p₃ + 1 - 1 = 0, p₃ = 0

₃₃ = 0, p₃ + q₃ – c₃₃ = 0, 0 + q₃ – 7 = 0, q₃ = 7

₁₅ = 0, p₁ + q₅ – c₁₅ = 0, 0 + q₅ - 0 = 0, q₅ = 0

₂₁ = p₂ + q₁ - c₂₁ = 1 + 2 – 4 = -1

₃₁ = p₃ + q₁ - c₃₁ = -2 + 2 – 2 = -2

₃₂ = p₃ + q₂ - c₃₂ = 0 + 3 – 7 = -4

₁₃ = p₁ + q₃ – c₁₃ = 0 + 7 – 4 = -3

₁₄ = p₁ + q₄ – c₁₄ = 0 - 1 – 1 = -2

₂₃ = p₂ + q₃ – c₂₃ = 1 + 7 – 1 = -7

₂₅ = p₂ + q₅ – c₂₅ = -3 + 0 – 0 = -3

₃₅ = p₃ + q₅ – c₃₅ = 0 + 0 – 0 = 0

Я получил таблицу, для которой все _ij  0 i = 1,m; j = 1,n

Оценки удовлетворяют условию оптимальности, следовательно решение

оптимально.