Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

«Тульский государственный университет»

Кафедра «Финансы и менеджмент»

Методические указания к

САМОСТОЯТЕЛЬНОЙ РАБОТЕ СТУДЕНТА

по дисциплине «ЭКОНОМЕТРИКА»

Направление подготовки: 080100 «Экономика» Специальности подготовки: 080105 «Финансы и кредит»,

080109 «Бухгалтерский учет и аудит», 080102 «Мировая экономика»

Форма обучения: очная

Тула 2011 г.

Методические указания составлены доц. Гучек Н.Е и обсуждены на заседании кафедры «Финансы и менеджмент» факультета Экономики и менеджмента,

протокол № 1_ от « _30_ » _августа_ 2011г.

зав. каф. __________________ Е.А Федорова

Методические указания пересмотрены и утверждены на заседании кафедры «Финансы и менеджмент» факультета Экономики и менеджмента,

протокол № __ от « __ » ______ 201__г.

зав. каф. __________________ Е.А Федорова

В соответствии с учебным планом студенты 3-го курса экономического

профиля по дисциплине «Эконометрика» должны выполнить две самостоятельные работы, где они должны показать умение применять знания, полученные на лекционных и практических занятиях в результате изучения данного курса.

Студент в результате изучения дисциплины должен:

з н а т ь:

- основные понятия, категории и инструменты эконометрики, ее роль и место в комплексе экономических задач;

- основные особенности ведущих школ и научных направлений;

- методы построения эконометрических моделей объектов, явлений и процессов.

у м е т ь:

- осуществлять поиск информации по полученному заданию, сбор и анализ данных для решения поставленных экономических задач;

- осуществлять выбор инструментальных средств для обработки экономических данных в соответствии с поставленной задачей, анализировать результаты расчетов и обосновывать полученные выводы;

- стоить эконометрические модели, анализировать и интерпретировать полученные результаты;

- прогнозировать на основе полученных моделей поведение экономических объектов, процессов на макро и микро уровнях.

в л а д е т ь:

- методологией эконометрического исследования;

- методикой построения эконометрических моделей;

- методами и приемами анализа экономических явлений и процессов с помощью эконометрических моделей;

- навыками самостоятельной работы и работы со специальными таблицами и литературой.

Задача самостоятельной работы – выработать у студентов твердые навыки исследования и решения определенного круга задач, привить способность к самостоятельному аналитическому мышлению и умению работать со справочной литературой и таблицами.

Самостоятельная работа № 2

Множественная регрессия

В множественном (многомерном) регрессионном анализе пытаются найти зависимость одной зависимой переменной от нескольких независимых: .

Связь между переменной Y и m независимыми факторами можно охарактеризовать функцией регрессии : которая показывает, каково будет в среднем значение переменной переменной Y, если переменные примут конкретные значения.

Линейная модель множественной регрессии имеет вид: .

Это уравнение содержит значения неизвестных параметров ( ). Эти неизвестные параметры (случайные величины) оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки.

Модель линейной регрессии, в которой вместо истинных значений параметров подставлены их оценки (а именно такие модели регрессии и применяются на практике), имеет в матричном виде следующее соотношение: ,

где Y – вектор зависимой переменной размерности (n 1), представляющий собой n наблюдений значений ;

Х – матрица n наблюдений независимых переменных , размерность матрицы Х равна (добавлен единичный столбец для определения );

А - подлежащий оцениванию вектор (матрица – столбец) неизвестных параметров в размерности ;

- вектор случайных отклонений (возмущений) размерности (n 1).

Таким образом, имеем следующие матрицы:

; .

Неизвестные параметры определяются с помощью МНК.

Рассмотрим решение типовых задач.

Задача 1. По 30 регионам известны следующие данные о годовом потреблении мяса на душу населения (кг) y, доходе на душу населения за год (тыс. руб.) х₁ и годовом потреблении рыбы на душу населения (кг) х₂:

; ; ; ; ; ;

; ; .

Необходимо найти:

1. Построить линейное уравнение множественной регрессии.

2. Найти коэффициент множественной детерминации, в том числе скорректированный. Сделать выводы.

3. Оценить значимость уравнения регрессии через F-критерий Фишера с вероятностью 0,95.

4. Оценить целесообразность включения в модель фактора х₂ после фактора х₁, используя частный F-критерий.

5. Определить частные коэффициенты корреляции и сделать выводы.

6. Определить частные средние коэффициенты эластичности и сделать выводы.

7. Предполагая прогнозные значения х₁=100 и х₂=35, найти с вероятностью 0,95 интервальную оценку прогнозного значения функции регрессии, а также доверительный интервал для индивидуального прогнозного значения потребления мяса.

8. Оценить вероятностью 0,95 доверительный интервал для значимого коэффициента регрессии.

Решение: 1.Линейное уравнение множественной регрессии y от х₁ и х₂ имеет вид .

Для расчета его параметров применим МНК. Система нормальных уравнений составит

Решим систему уравнений, используя определители

, , ,

где - определитель системы;

а, b₁, b_2, - частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными правой части системы.

=181870920, а=8353465200, b₁=29743200, b₂=-5904900,

,

,

.

Получаем уравнение

С увеличением годового дохода на душу населения на 1 тыс. руб. годовое потребление мяса -у возрастает на 0,16 кг при фиксированном значении годового потребления рыбы; с увеличением годового потребления рыбы на 1 кг годового потребление мяса у снижается на 0,03 кг при фиксированном значении годового душевого дохода.

2. Коэффициент множественной детерминации определяем на основе парных коэффициентов корреляции по следующей формуле:

Вычислим парные коэффициентов корреляции

,

,

,

.

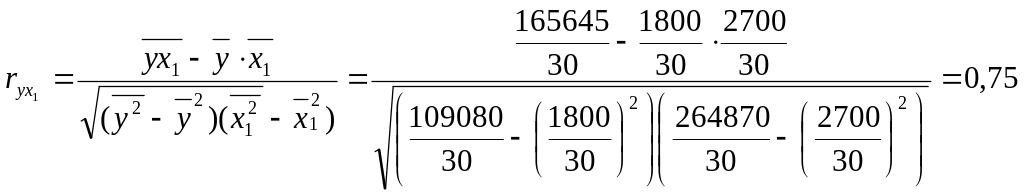Коэффициент множественной корреляции составил: R=0,75018.

Значимость у от х₁ и х₂ характеризуется как тесная; вариация потребления мяса на душу населения на 56% определяется вариацией учтенных в уравнении факторов – дохода на душу населения и годового потребления рыбы. Прочие факторы, не включенные в модель, составляют 44% от общей вариации у.

Скорректированный коэффициент множественной детерминации определяется по формуле

,

где n – число наблюдений;

m – число параметров при переменных х.

.

3.Значимость уравнения регрессии оцениваем через общий F-критерий Фишера:

.

Табличное значение критерия при уровне значимости =0,05 и числе степеней свободы 2 и 27 равно F_табл=3,35. Сравнивая F_табл и F_факт, делаем вывод о статистической значимости уравнения в целом.

4. Частные F_xi-критерий оценивают целесообразность включения в модель одного фактора после других. Частный F_х2-критерий оценивает целесообразность включений х₂ после фактора х₁:

.

Табличное значение критерия при уровне значимости  =0,05 и числе степеней свободы 1 и 27 равно F_табл=4,21. Сравнивая F_табл и F_х2, делаем вывод о нецелесообразности включения х₂ после фактора х₁, так как F_х2< F_табл..

5.Частные коэффициенты корреляции рассчитаем по рекуррентной формуле:

,

.

Значимость коэффициентов парной и частной корреляции отличаются по абсолютной величине из-за наличия связи между факторами (r_х1х2=-0,65).

6.Частные средние коэффициенты эластичности используются для характеристики относительной силы влияния х₁ и х₂ на у.

.

;

.

С увеличением годового душевого дохода населения на 1% от среднего уровня годовое потребление мяса возрастает на 0,245% от своего среднего уровня при фиксированном значении годового потребления рыбы. С увеличением на 1% от среднего уровня годового потребления рыбы годовое потребление мяса снижается на 0,011% от своего среднего уровня при фиксированном значении годового душевого дохода. Сила влияния годового дохода х₁ на годовое потребление мяса больше, чем сила влияния годового потребления рыбы х₂.

7.Определяем точечный прогноз годового потребления мяса путем подстановки в уравнение регрессии прогнозных значений факторных признаков (х₁=100 и х₂=35):

.

Стандартная ошибка регрессии (S) определяется по формулам:

или ;

.

Стандартная ошибка составляет 7% от среднего значения результативного признака.

Ошибку прогнозного значения функции регрессии получим по формуле ,

где ; ; ; , где - присоединенная матрица (Х^ТХ);

,

где а_ij – элементы матрицы, получаемые как ;

М_ij - матрица, получаемая вычеркиванием из (Х^ТХ) i-ой строки и j-го столбца.

.

Табличное значение критерия Стьюдента при уровне значимости =0,05 и числе степеней свободы n-m-1=27 равно: t_таб=2,05.

Интервальная оценка прогнозного значения функции регрессии определяется по формуле:

,

,

,

.

Определяем доверительный интервал для индивидуального прогнозного значения потребления мяса по формуле

,

,

,

,

.

Годовое потребление мяса будет находиться в интервале от 49,1 до 73,1 кг при душевом доходе 100 тыс.руб. и годовом потреблении рыбы 35 кг.

Доверительный интервал коэффициента регрессии определяется на основе стандартной ошибки ( ):

.

В уравнении коэффициент регрессии b₁ статистически значим, а коэффициент регрессии b₂ статистически незначим. Стандартную ошибку коэффициента регрессии ( ) можно определить разными способами:

а) , ,

,

, ;

б) ;

в)

г) ,

где а₁₁ – диагональный элемент присоединенной матрицы (а₁₁=14440);

- определитель исходной матрицы факторов;

.

Получим доверительный интервал коэффициента регрессии b₁:

.

С вероятностью 0,95 коэффициент регрессии будет находиться в интервале

.

Интервал не содержит нулевого значения, следовательно, коэффициент регрессии является статистически значимым.

Задача 2

По данным в таблице 1 изучается зависимость индекса человеческого развития y от переменных:

x₂ - расходы на конечное потребление в текущих ценах, % к ВВП

x₃ –расходы домашних хозяйств, % к ВВП

Исходные данные:

таблица 1

Страна	y	x2	х3
Австрия	0,904	75,5	56,1
Австралия	0,922	78,5	61,8
Белоруссия	0,763	78,4	59,1
Бельгия	0,923	77,7	63,3
Великобритания	0,918	84,4	64,1
Германия	0,906	75,9	57,0
Дания	0,905	76	50,7
Индия	0,545	67,5	57,1
Испания	0,894	78,2	62,0
Италия	0,9	78,1	61,8
Канада	0,932	78,6	58,6
Казахстан	0,74	84	71,7
Китай	0,701	59,2	48,0
Латвия	0,744	90,2	63,9
Нидерланды	0,921	72,8	59,1
Норвегия	0,927	67,7	47,5
Польша	0,802	82,6	65,3
Россия	0,747	74,4	53,2
США	0,927	83,3	67,9
Украина	0,721	83,7	61,7
Финляндия	0,913	73,8	52,9
Франция	0,918	79,2	59,9
Чехия	0,833	71,5	51,5
Швейцария	0,914	75,3	61,2
Швеция	0,923	79	53,1