Лаборотонрая работа М-5

Изучение законов динамики вращательного движения твердого тела вокруг неподвижной оси на маятнике обербека

1. Цель работы:

Экспериментальная проверка зависимостей между физическими величинами, характеризующими вращение твердого тела вокруг неподвижной оси.

2. Приборы и принадлежности: маятник Обербека, комплект перегрузов, миллисекундомер.

3. Описание экспериментальной установки и подготовка установки к измерениям.

Маятник Обербека представляет собой инерционное колесо в виде крестовины (рис.1). На четырех взаимно перпендикулярных стержнях могут перемещаться грузы m´. На горизонтальной оси крестовины имеется двухступенчатый диск радиуса r₁ и r₂, на который наматывается нить. Один конец нити прикреплен к диску, а на втором конце нити, перекинутой через неподвижный блок, подвешен груз m, состоящий из основного груза, на который могут помещать добавочные грузы. Под влиянием падающего груза нить разматывается с диска и вызывает ускорение вращения крестовины вокруг неподвижной горизонтальной оси. Маятник с помощью неподвижного кронштейна установлен на вертикальной колонне, на которой нанесена миллиметровая шкала для подсчета длины перемещения грузов. На вертикальной колонне (1) прикреплены два кронштейна: нижний (2) неподвижный и верхний (3) подвижный. Подвижный кронштейн (3) можно перемещать вдоль колонны (1) и фиксировать его в любом положении, определяя таки образом длину пути Н грузов. Установка снабжена двумя фотоэлектрическими датчиками (4 и 5), вырабатывающими электроимпульсы соответственно начала и конца измерения времени движения грузов. Маятник с грузами удерживается в состоянии покоя с помощью тормозного электромагнита. На основании колонны жестко закреплен миллисекундомер (6), к которому подключены фотодатчики. Само основание прибора снабжено регулируемыми ногами (7), обеспечивающими горизонтальную установку прибора.

Работа с прибором допускается только при наличии заземления.

На установке можно провести прямое измерение времени движения груза массой m на пути Н и получить, таким образом, множество значений времени при различных m,H,ρ и радиусах намотки r₁ и r₂ и различных положениях грузов m.

Ясно, что проведение измерений времени при всех возможных комбинациях указанных величин- нереальная задача. Кроме того, неясно что с результатами делать дальше и что с их помощью можно определить.

Ответы на последние вопросы дает теоретическая модель экспериментальной ситуации. Она же позволяет составить план измерений и обработки результатов.

Любая теоретическая модель дает приближенное описание экспериментальной ситуации, поскольку пренебрегает влияниям многих реально имеющих место эффектов.

Ниже рассмотрены две модели возрастающей сложности. Чем сложнее модель, тем сложнее с ней работать.

При выполнении работы вы должны вначале выполнить задания 1.1 – 1.4* модели I и только после этого вместо задания модели 1.5* можно выполнять задание 2.1** модели II.

В модели I сформулированы и обязательные задания и необязательные, которые помечены звездочкой (*), и за которые вы получаете дополнительные баллы к рейтингу. Задание модели II, помеченное двумя звездочками (**), необаятельное, но оценивается наиболее высоко.

Ниже дается необходимая для выполнения работы и обработки результатов информация по каждой модели.

Внимание! Для отчета по работе необходимо изучить также материал приложений.

Модель I. В этой модели считается, что трение в оси блока (8) отсутствует, этот блок невесом, а момент сил трения Μ_тр, в оси блока с крестовиной не зависит от угловой скорости вращения. В этих условиях ускорение груза массой m постоянно на всем отрезке Н и равно:

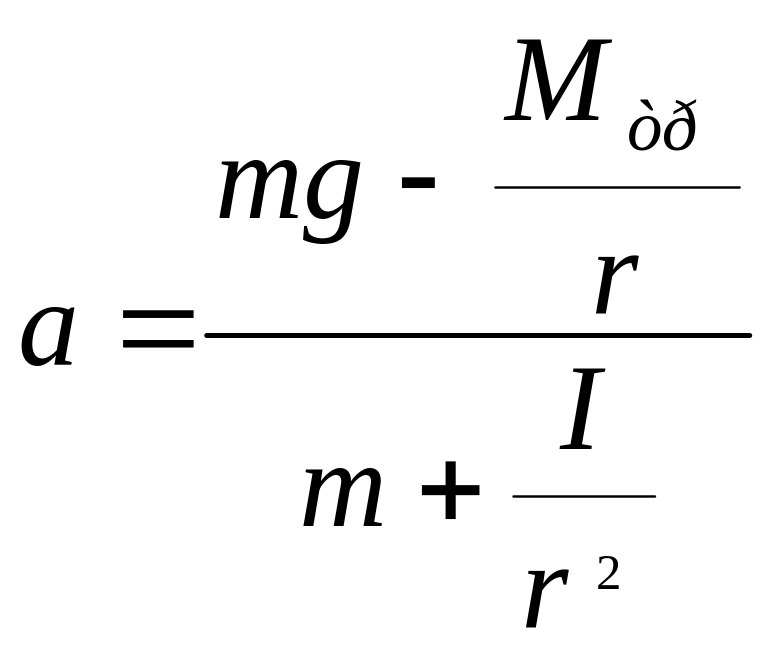
где r – радиус намотки, I – момент инерции блока с крестовиной (r=r₁ либо r₂, I - определяется положением грузов массой m´ каждый и моментом инерции блока без грузов I₀).

С другой стороны, на основании кинематических соображений, если а – постоянная величина, то , где Н – задаваемое перемещение груза, t – измеренное время его движения. Тогда

(1.1) .

формула (1.1) является основной для работы в рамках модели I.

Задание 1.1 Проверка независимости момента сил трения Μ_тр от угловой скорости вращения блока

а) освободите стержни крестовины от грузов m’ и убедитесь, что блок с крестовиной находится в безразличном равновесии в любом из возможных положений, когда нить с грузом m не прикреплена к блоку. Если это не так, то добейтесь состояния безразличного равновесия путем незначительного ввинчивания или вывинчивания стержней крестовины в ось блока. В дальнейшем следует строго следить за тем, чтобы эти условия не нарушались следствии случайно возможных вращений стержней в гнездах, особенно при последующем закреплении на стержнях грузов массой m’. Закрепите грузы m’ на указанном преподавателем расстоянии ρ оси и опять проверьте, находится ли система в состоянии безразличного равновесия. Если это не так, небольшими смещениями грузов на стержнях крестовины добейтесь, чтобы это состояние имело место. Последующие измерения временно нужно будет провести не мене чем при 5 значениях Н, поэтому согласуйте с преподавателем рабочий интервал значений Н и шаг измерений Н в пределах этого интервала. Установите кронштейн (3) на минимальное значение Н из рабочего интервала. Закрепите один конец диска нити на диске радиуса r=r₁ или r=r₂ по указанию преподавателя, перекиньте нить с подвешенным на другом её конце грузом (основной груз + указанное преподавателем число добавочных грузов) через неподвижный блок и добейтесь, чтобы нижний край груза m совпал с чертой на корпусе верхнего фотодатчика (4).

Идея проверки

Если Μ_тр не зависит от угловой скорости вращения, то при различных Н правая часть формулы (1.1) постоянна и зависимость (t²) от H должна быть линейной:

(1.1.1)

Поэтому, если нанести экспериментальные точки (Н_i,t_i²) на координатную плоскость, по оси абсцисс которой откладывается Н, а на оси ординат – (t²), то экспериментальные точки должны лежать на прямой;

а) проведите измерения t_i при различных H_i (при каждом H_i не менее 3-х раз и в качестве t_i примите среднее из полученных значенийменее 3-х раз и в качестве лежать на прямойой накладыи различных Н правая часть формулы ()е грузом=р1 или ррр=р2 по указанно) и убедитесь визуально в линейной зависимости (t²) от (Н);

б) более строгого рассмотрения требует привлечение метода наименьших квадратов (МНК) и критериев согласия, например Х² – критерия Пирсона.

Обозначим в (1.2) t²=y, Н=х, 2/а=k. Тогда y=kx

В приложении III показано, что наилучшее в смысле МНК значение коэффициента k для зависимости имеет вид:

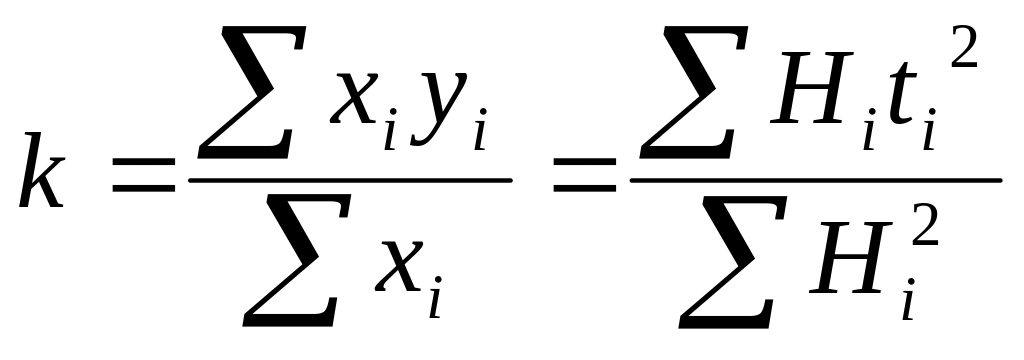(1.1.2)

где суммирование производится по всем задаваемым H_i и измеренным t_i. Найдите k по формуле (1.3) и проведите на координатной плоскости (Н,t²) эту наилучшую в смысле МНК прямую. Для применения Х² – критерия следует далее вычислить величину

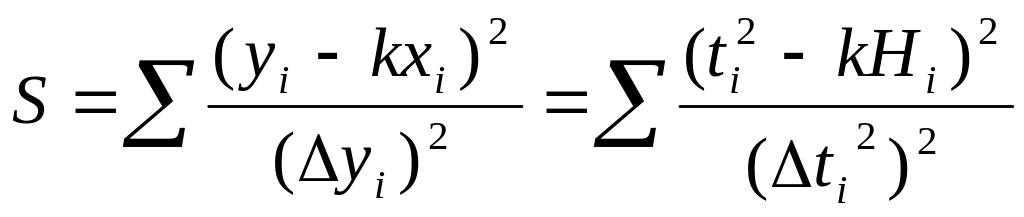
где y_i=2t t_i – погрешность в определении величины y_i=t_i² в i-м измерении. Поскольку t_i определяется прямым образом, то

При использовании электронных измерителей времени с цифровой индексацией можно принять t_{i разб} >> t_{i град} и t_{i отсч}. Поэтому t_{i разб} ≈ t_i

Тогда для величины y_i=t_i² погрешность будет равна

y_i=2t_i t_i

Таким образом

Затем величину S сравните с табличным значением для Х² – критерия так, как это делалось в работе (М-1), и найдите уровень значимости проверяемой гипотезы о независимости Мтр от угловой скорости вращения.

Задание 1.2  Оценка момента сил трения М_тр.

Основная идея оценки состоит в следующем. Пусть m_min – минимальная масса груза m, при которой система приходит в движение, т.е. при m < m_min система покоится. Тогда из формулы (1.1) при a = 0 получим

М_тр= m_min gr, (1.2.1)

где r – радиус намотки на блоке с крестовиной. Поскольку даже основной груз без добавочных уже приводит систему в движение, то для определения m_min используется другая нить с очень легкой платформой, на которую можно помещать дополнительные грузы массы из набора, находящегося на рабочем месте.

а) закрепите нить с платформой на меньшем радиусе r₁ ступенчатого блока с крестовиной, перекиньте нить через неподвижный блок (8) и кладите на платформу дополнительные грузы до тех пор, пока система не придет в движение. Проделайте опыт несколько раз, усреднив значение m_min. По формуле (1.2.1), положив r=r₁, найдите М_тр;

б) повторите измерение при большом радиусе намотки r₂ и опять найдите М_тр по формуле (1.21), положив r=r₂;

в) сравните полученные в пунктах а) и б) значение М_тр и письменно сформулируйте выводы.

Задание 1.3  Определение момента инерции ступенчатого блока с крестовиной и момента сил трения

Допустим, что мы измерили t₁, движение груза массой m, на заданном перемещении H при радиусе намотки r₁, а затем время t₂ движения того же груза, на том же перемещении при радиусе намотки r₂. Положение грузов m’ в обоих случаях не изменилось. Тогда при постоянстве М_тр имеем согласно формуле (1.1)

;

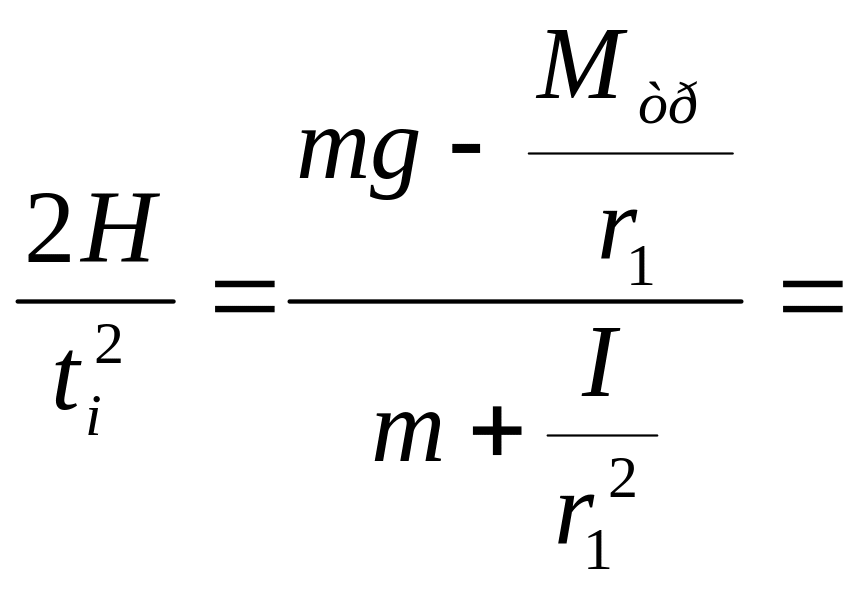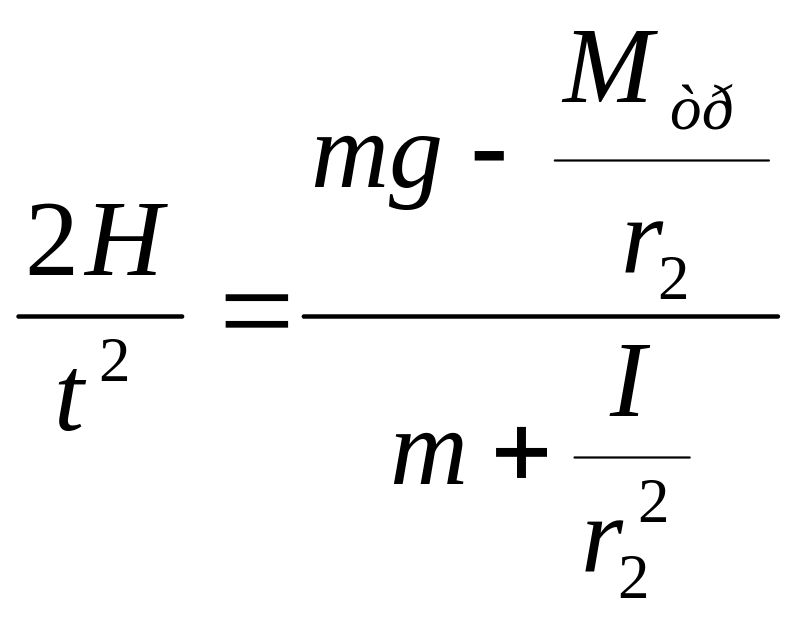
Решая систему, находим

(1.3.1)

Таким образом, для определения момента инерции и момента сил трения имеем следующую программу действий:

а) согласуйте с преподавателем выбор H и m. Лучше, если H будет как можно больше, т.е. в качестве H можно принять максимальное H из рабочего интервала задания 1.1;

б) измерьте несколько раз время движения груза при радиусе намотки r=r₁ и найдите среднее значение t₁;

в) измерьте несколько раз время движения того же груза при радиусе намотки r=r₂ и найдите среднее значение t₂;

г) по формулам (1.3.1) найдите I и М_тр;

д) повторите измерение п.п. б) – г) при другим массах груза m (не менее трех значений) и усредните полученные результаты для I и М_тр;

е) вычисление погрешностей I и М_тр исходя из формулы (1.3.1) достаточно громоздко и малопоучительно, поэтому примите в качестве погрешностей I и М_тр погрешность разброса при различных массах грузов m;

ж) сравните М_тр со значением найденным в предыдущем задании и сформулируйте письменно причины возможных расхождений.

Задание 1.4* Проверка аддитивности момента инерции

Пусть I₀ – момент инерции блока с крестовиной без грузов. Если каждый груз считать материальной точкой, находящейся на расстоянии r – от оси, то вследствие аддитивности момента инерции состоящей в том, что момент инерции составного тела равен сумме моментов инерции частей, момент инерции I при наличии грузов на крестовине будет равен

I=I₀+4m’ρ² (1.4.1)

Если учесть, что фактически каждый груз является полым цилиндром длиной L, внешним радиусом r и внутренним r’, то вместо (1.4.1) будем иметь

Целью данного задания является проверка формулы (1.41) или (1.42) вытекающих из аддитивности момента инерции.

а) момент инерции крестовины с грузом был определен в предыдущем задании. Поэтому тщательно определите величину ρ. При строгой симметрии системы величина ρ для всех грузов должна быть одной и той же. Реально, однако, когда при выполнении предыдущих упражнений пришлось добиваться без различного равновесия системы, расстояние ρ для различных грузов оказались слегка различными. Можно показать, что при небольших различиях ρ для различных грузов формулы (1.41), (1.42) нужно подставлять среднее арифметическое отдельных значений. Рекомендуем это сделать самостоятельно в качестве упражнений;

б) снимите грузы m’ с крестовины и повторите все измерения предыдущего задания, определив момент инерции I₀ крестовины без грузов и момент силы трения М_тр в этом случае;

в) подставляя в формулы (1.41) и (1.42) значение I из предыдущего задания и I₀, ρ, проверьте выполнение условия аддитивности. Сформулируйте письменно вывод о том, какая из формул точнее;

г) сравните значение М_тр при наличии грузом m’ на крестовине и значение М_тр, когда они отсутствуют. Опыт показывает, что момент сил трения в оси любого блока можно представить в виде суммы двух частей: приблизительно постоянной, не зависящей от нагрузки на ось составляющей и составляющей, пропорциональной нагрузке на ось блока (реакции оси).

Рекомендуем самостоятельно продумать причины возникновения этих составляющих и обсудить их с преподавателем.

При выполнении задания 1.3 изменялась масса m приводящих систему в движение грузов, а также радиус намотки. Это приводит, как показано в приложении II к очень незначительному изменению реакции оси и поэтому можно было считать М_тр все время постоянным. Напротив, когда грузы m’ сняты с крестовины, нагрузка на ось изменяется значительно, поэтому изменяется значительно и та составляющая М_тр, которая пропорционально нагрузке.

Попробуйте самостоятельно, на основе результатов предыдущих заданий, пользуясь консультацией преподавателя, оценить ту или другую составляющие М_тр.

Задание 1.5* Определение момента инерции ступенчатого блока с крестовиной и момента сил трения по методу наименьших квадратов

Перепишем формулу (1.1) в виде

Обозначим

m(g-a)=Z, a=x, ,

Тогда получим

Z=Ax+B (1.5.1)

Основная идея определения момента инерции состоит в следующем. Определяя время движения груза t_i на заданном отрезке H при различных значениях m_i массы груза, можно найти

и Z_i=m_i(g-a_i)

Где g= 9,8 м/с² – ускорение свободного падения. Зависимость между Z и Х согласно (1.5.1) линейная. Соответствует ли это действительности? Можно убедиться визуально, нанеся на координатную плоскость (Х,Z) экспериментальные точки. Коэффициент А и B можно найти по МНК (приложение IV).

; (1.5.2)

Где

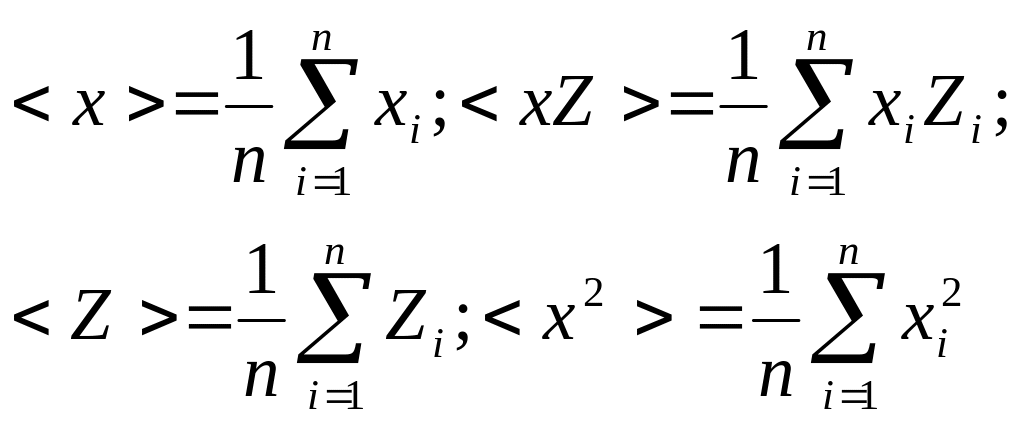
n – число измерений

Таким образом, нужно реализовать следующую программу:

а) установите кронштейн 4 на наибольшем возможном расстоянии Н из рабочего интервала задания 1.1. Радиус намотки (r₁ или r₂) выберите по указанию преподавателя;

б) измерьте время движения основного груза на заданном расстоянии Н несколько раз и результат усредните. Обозначьте это среднее время t₁ а массу основного груза – m₁, найдите

в) добавьте к основному грузу один добавочный, повторите измерение времени и найдите:

где t₂ – среднее время движения в этом случае, m₂ – масса основного грузка с добавочным;

г) добавьте еще один добавочный груз, найдите t₃, x₃, Z₃ и т.д.;

д) на координатной плоскости (x,Z) нанесите экспериментальные точки (x_i,Z_i) и оцените визуально лежат ли они на прямой. Результаты удобно организовывать в виде следующей таблицы

H=…м, r=…м

Время движения (с)	ti (c)	(к*с-2)	mi (кг)	(H)	(м2с-4)	Zixi (Н*м*с-2)
…	…	…	…	…	…	…

е) по формулам (1.5.2) найдите А и B. Проведите, используя найденные значения на плоскости (x,Z) наилучшую прямую согласно уравнению 1.5.1;

ж) найдите момент инерции крестовины и момент силы трения по формулам

I=Ar²; M_тр=Br;

з) сравните найденное значение М_тр с тем, которое было получено в задании 1.2. Сформулируйте причины возможных отличий;

и) строгие формулы для расчета погрешностей определения величин А и B по МНК громоздки и малонаглядны. Поэтому для оценки этих погрешностей можно воспользоваться следующим приближенным графическим способом.

Для оценки погрешности величины B смещайте параллельно самой себе вниз наилучшую прямую, построенную на координатной плоскости (x,Z) в пункте e) до тех пор, пока выше ее не окажется примерно вдвое больше точек, чем снизу. Затем следует смещать ее вверх, пока снизу не окажется примерно вдвое больше точек, чем сверху. Расстояние между этими прямыми по вертикали обозначим ₁B. Тогда погрешность в определении B равна:

Считая для простоты, что радиус намотки r известен со значительно меньшей погрешностью, получим:

М_тр=r B

Для оценки погрешности в определении величины А участок оси Х, на котором находится экспериментальная точка, делится на три равные части и средний участок в дальнейшей работе не участвует. Поворачивайте наилучшую прямую так, чтобы на левом участке ее оказалось примерно вдвое больше точек, чем под ней, а на правом – наоборот. Затем прямая поворачивается так, чтобы на левом участке примерно 2/3 точек лежали ниже прямой, а на правом – выше ее.

1) Пусть ₁А – разница в угловых коэффициентах этих прямых. Тогда погрешность в определении А равна

и погрешность в определении момента инерции:

I=r² A

Найдите М_тр и I и запишите окончательные результаты для I и М_тр

Модель 2. Эта модель отличается от модели 1 тем, что в ней учитывается момент сил трения в оси блока (8) – М’_тр. Нагрузка на ось этого блока значительно меньше, чем на ось блока с крестовиной, поэтому при одинаковой конструкции узла трения можно пренебречь той составляющей М’_тр, которая пропорциональна нагрузке, и считать, что М’_тр –постоянная величина, обусловленная креплением оси. В этих условиях теория приложения II дает следующее выражение для ускорения груза

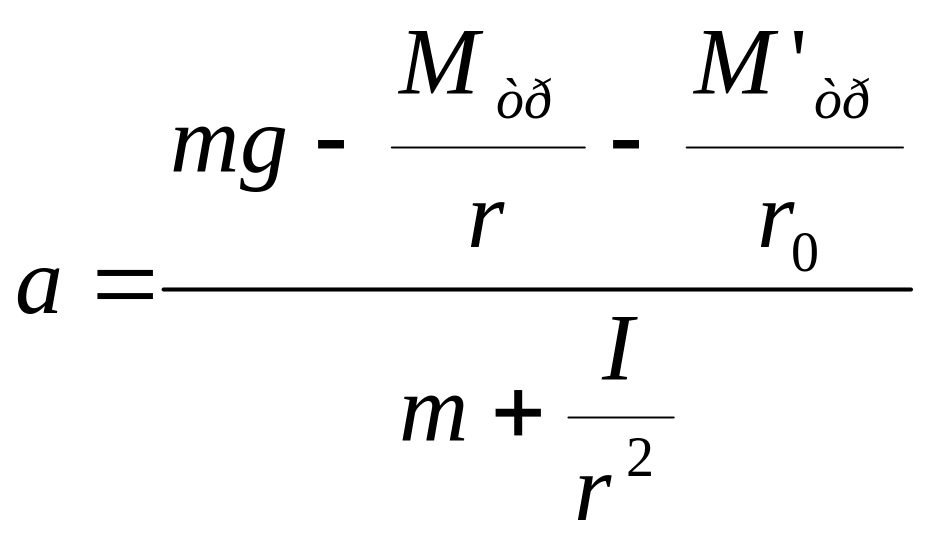
(2.1)

где - ускорение груза, которое при независимости М_тр и М’_тр от угловой скорости вращения будет при заданных m, иии, ррр постоянны. Преобразуем (2.1) следующим образом

Введем обозначения

Тогда получим

Z=gy+Ax+B (2.2)

Задавая разные значения массы грузов m_i=y_i и определяя ускорения a_i=x_i и Z_i=y_ix_i можно с помощью МНК определить наилучшие значения констант g, A, B соответствующие линейной зависимости П.2, решив следующую систему уравнений, которую рекомендуем получить самостоятельно:

где n - число значений масс грузов m_i при которых производились опыты.

С учетом вышеприведенных обозначений систему можно представить в виде:

(2.3)

Таким образом, нужно реализовать следующую программу.

Задание 2.1** Определение ускорения свободного падения, момента инерции блока с крестовиной и момента сил трения в осях блока.

а) установите грузы m` на крестовине так, как в задании 1.3 и добейтесь безразличного равновесия системы, когда к ней не прикреплена нить;

б) закрепите нить на блоке радиусом r=r₁ и измерьте несколько раз время движения основного груза на заданном расстоянии Н. Обозначьте среднее время t₁, массу основного груза m₁ и найдите

в) повторите измерения, используя основной груз + один добавочный, найдите t₂ и , суммарную массу основного груза и одного добавочного обозначьте m₂;

г) повторите измерения, используя основной груз + два добавочных суммарной массой m₃, найдите t₃ и и т.д.

д) поставьте численные значения в систему (2.3) и решите систему, найдя А,g,В;

с) найдите момент инерции системы

ж) повторите измерения п.п. б-г при радиусе намотки r=r₂, вновь подставьте численные значения в формулу (2.3), найдя в результате решения системы значения постоянных А`,g`,В` и момента инерции ;

з) усредните результаты для I и g, соответствующие r=r₁ и r=r₂. Сравните значение I с найдены в задании 1.3, а значении g – со стандартным g=9.81м/с²;

и) решая систему уравнений

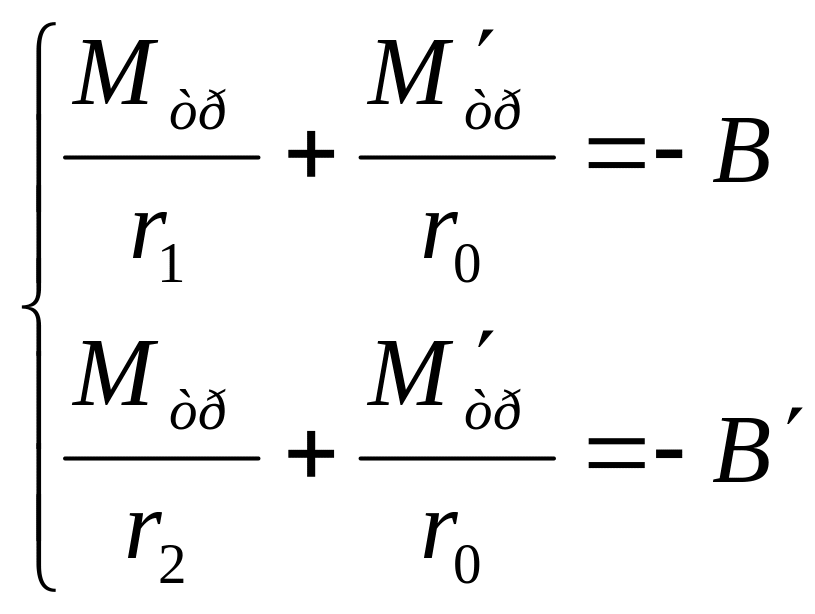
найдите моменты сил трения в осях обоих блоков. Сравните результат для М_тр с тем, который был получен в задании 1.3 и письменно сформулируйте выводы;

к) поскольку расчет погрешностей на основе формул (2.3) громоздок и малопоучителен, рассчитайте погрешности для I и g как погрешности разброса при r=r₁ и r=r₂. В качестве погрешностей М_тр и М_тр примите значение, найденное в задании 1.3

Приложение 1. Основные сведения по динамике вращательного движения твердого тела вокруг неподвижной оси.

1. Движение твердого тела, при котором две его точки остаются неподвижными, называется вращением тала вокруг неподвижной оси. Прямая, соединяющая эти точки, называется ось вращения тела. При вращении вокруг неподвижной оси все точки тела описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны к ней. Положение твердого тела в пространстве полностью определяется значением φ угла поворота тела из некоторого начального положения.

2. Для характеристики быстроты вращения тела вокруг оси служит угловая скорость. Угловой скоростью называется быстрота изменения (а точнее производная) угла поворота φ по времени:

(П 1.1)

Вращение считается равномерным, если ω=const.

3. --- величиной, характеризующей быстроту (и направление) изменения угловой скорости , производная от угловой скорости или вторая производная угла поворота по времени

Модуль угловой скорости и углового ускорения связаны соответственно с модулями линейной скорости V и линейного ускорения a соотношениями:

(П 1.3)

где r- радиус окружности вращения.

4. Моментом силы относительно неподвижной точки (полюса) называется векторная величина , равная векторному произведению радиус-вектора , проведенного из этой точки в точку приложения силы, на вектор силы :

(П 1.4)

Модуль момента силы

(П 1.5)

где - угол между векторами и , а – плечо силы.

При переносе точки приложения силы вдоль линии её действия момент той силы относительно одной и той же неподвижной точки не изменяется. Если линия действия силы проходит через точку С (рис. П.1), то момент силы относительно этой точки равен нулю.

5. Момент силы относительно неподвижной оси OZ называется скалярная величина М_z, равная проекции на эту ось вектора момента силы относительно произвольной точки на оси. Значение М_z не зависит от выбора положения точки на оси.

Главный момент относительно неподвижной оси системы сил равен алгебраической сумме моментов относительно этой оси всех сил.

6. Моментом инерции математической системы относительно неподвижной оси OZ называется физическая величина I_z, равная сумме произведений масс всех n материальных точек на квадраты расстояний по оси:

(П 1.6)

где m_i и ρ_i – масса i-ой точки и ее расстояние от оси.

Момент инерции тела

(П 1.7)

где d=D·dV - масса малого элемента объема тела; dV – плотность; ρ – расстояние от элемента dV до оси OZ.

Для однородного тела (D=const)

(П 1.8)

Момент инерции тела является мерой инертности во вращательном движении.

7. Теорема Гюйгенса-Штейнера: Момент инерции тела I относительно произвольной оси равен сумме момента инерции тела I_с относительно оси, проходящей через центр масс тела параллельно данной оси, и произведения массы тела m на квадрат расстояния d между осями:

(П 1.9)

8. Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси имеет вид:

(П 1.10)

где I – момент инерции тела (системы тел) относительно оси вращения: М – сумма проекций на ось вращения моментов всех внешних сил, действуюших на тело (систему); ε – угловое ускорение.

ПРИЛОЖЕНИЕ 2. Применение законов динамики вращательного и поступательного движения при наличии идеальных связей.

Рассмотрим систему, состоящую из блока 1 с моментом инерции I, который может вращаться вокруг неподвижной горизонтальной оси О₁ и блока 2 с моментом инерции I`, вращающегося вокруг оси О<sub>2</sub>. Радиусы блоков обозначим r и r<sub>0</sub> соответственно. Невесомая нерастяжимая нить (идеальная связь) приводит блоки во вращение посредством привязанного к ней груза массой m. В осях блоков действуют моменты сил трения М<sub>тр</sub> и М`_тр, и – силы реакций осей блоков. Вследствие невесомости нити , . Запишем основное уравнение динамики вращательного движения для каждого блока, учитывая, что моменты и , и равны нулю:

где ε, ε` – угловые ускорения блоков. Второй закон Ньютона, записанный для груза массой m в проекции на вертикально вниз направленную ось, имеет вид:

Если проскальзывание нерастяжимой нити по блокам отсутствует, то , . Тогда для движения системы мы имеем следующую систему уравнений:

ф

Переход от фигурирующих в уравнениях динамики вращательного движения угловых ускорений к ускорению груза оправдывается тем, что ускорение груза легче экспериментально определить на основе прямых измерений времени движения груза.

Выражая Т₁, из последнего уравнения, подставляя во второе, и выражая из него Т₂, которое затем подставим в первое уравнение, получим следующее выражение для ускорения груза

(*)

Поскольку формула (*) является следствием законов динамики вращательного и поступательного движения, то ее экспериментальная проверка является одновременно и проверкой правильности применения этих законов для данной экспериментальной ситуации. Любая экспериментальная ситуация описывается в рамках некоторой модели, в которой пренебрегается влиянием реально имеющих место в действительности эффектов. Формула (*) и дает пример такого описания, в котором масса нити считается пренебрежимо малой, нить считается нерастяжимой, скольжение нити по блокам отсутствует, сопротивлением воздуха при выводе формулы (*) мы также пренебрегли. В работе используются еще более простые модели 1 и 2.

Во-первых, в обеих моделях масса блока 2 считается пренебрежимо малой по сравнению с массой блока 1. При сравнимых по величине радиусах r и r₀ это позволяет пренебречь слагаемым по сравнению с . Тогда

(**)

Моменты сил трения, во-вторых, считаются не зависящими от угловых скоростей вращения. Это позволяет считать при заданной массе груза m и фиксированном моменте инерции I ускорения постоянным и находить его из кинематического соотношения

где t – время движения груза m на заданном перемещении Н (подразумевается, конечно, что движение начинается из состояния покоя).

Моменты сил трения в осях блоков М_тр и М`<sub>тр</sub> каждый может быть представлен в виде суммы двух составляющих: постоянной, обусловленной особенностями крепления оси в подшипниках и переменной, зависящей от реакции и осей. В реальной установке масса груза m значительно меньше массы блока М<sub>1</sub>, поэтому R`<<R и можно, следовательно, полагать, что М`тр – постоянная величина.

Именно и это предполагается в модели 2. Кроме того, по той же причине сила R при изменении массы m грузов также изменяется незначительно и при различных m, но при фиксированной массе М₁ блока, М_тр остается постоянным. Перечисленные выше предположения вместе с формулой (**) и дают модель 2.

В модели 1 используются дальнейшие упрощения: предпологается, что трение в оси блока 2 вообще отсутствует.

Тогда имеем

(***)

Рекомендуем самостоятельно сформулировать условия, при которых это предположение оправдано, если пологать, что конструкции узла крепления осей блоков устроены одинаково.

ПРИЛОЖЕНИЕ 3. МНК для зависимости y=kx.

Задача состоит в том, чтобы подобрать такое значение k, при котором прямая у=kх наилучшим образом аппроксимировала экспериментальные результаты (т.е. наиболее близко подходила к экспериментальным точкам). Идея метода МНК в том, что значение коэффициента k будет оптимальным, если сумма квадратов разностей экспериментальных значений y_i и значений y`<sub>i</sub>, вычисленных по формуле y`_i =kх _i минимальная:

Условие экстремума функции дает

откуда

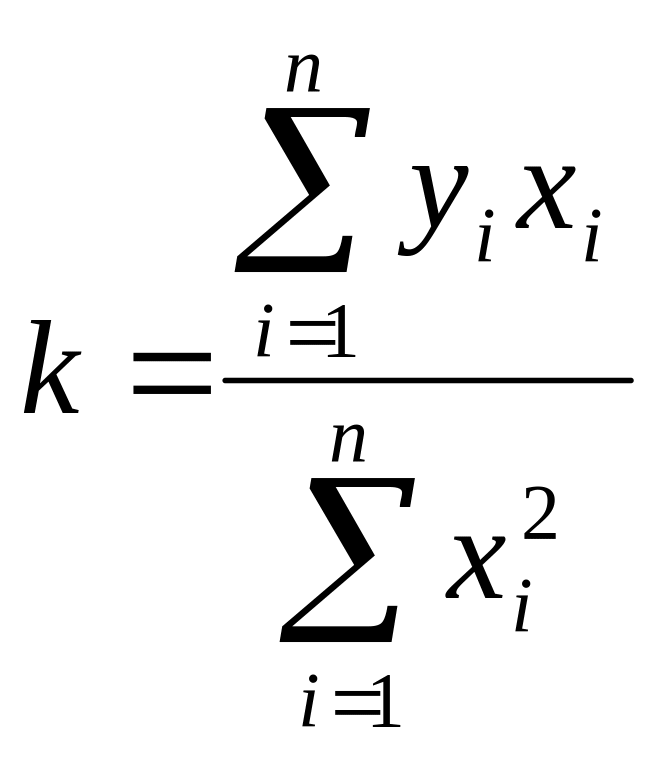
Вычисления по методу наименьших квадратов удобно организовать в виде таблицы.

i	xi	yi	xi2	xiyi
1 . . . n	x1 . . . xn	y1 . . . yn	x12 . . . xn2	x1y1 . . . xnyn

ПРИЛОЖЕНИЕ 4. МНК для зависимости Z=Ах+В

Рассуждая таким же образом, как и в Приложении 3 для нахождения оптимальных значений коэффициентов А и В минимизируем формулу

Запишем условие минимума

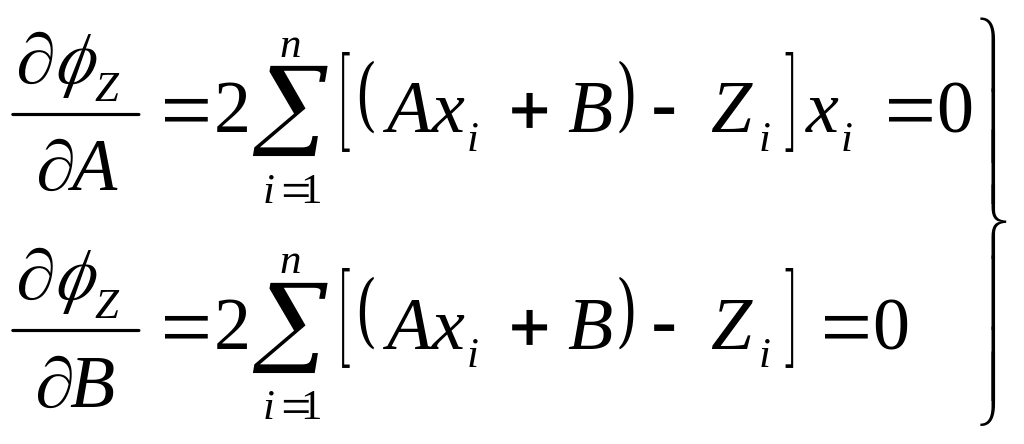
Сократив каждое уравнение системы на 2 и раскрыв скобки, получим

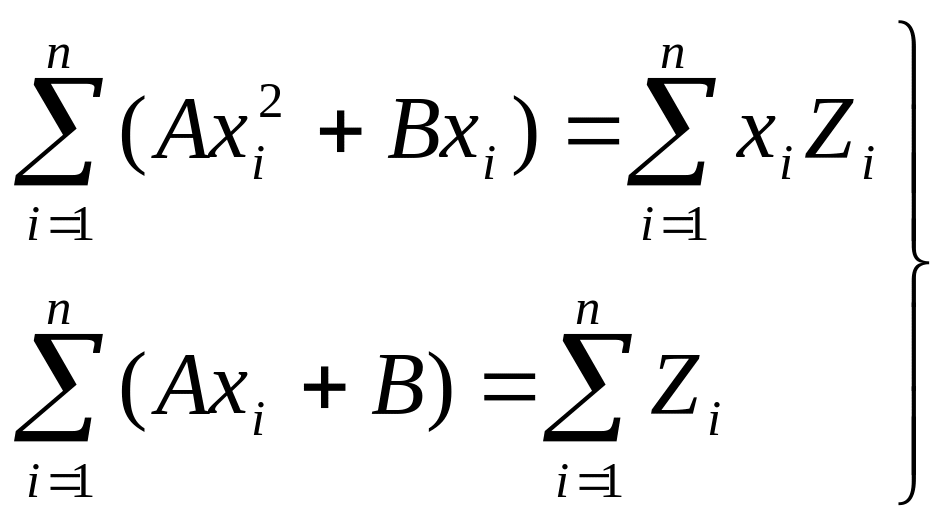
Введем следующие обозначения:

Тогда система примет вид:

Решив систему, получим

ПРИЛОЖЕНИЕ 5. Момент инерции цилиндра.

При определении момента инерции I_к крестовины с грузами m` по формуле (1.4.1) каждый из четырех грузов рассматривался как материальная точка. На самом деле каждый груз представляет из себя однородный полый цилиндр, ось вращения которого проходит через центр крестовины (рис. П 5.1) перпендикулярно к его продольной геометрической оси.

Выделим мысленно бесконечно короткий цилиндрик с массой dm`, находящийся от оси вращения на расстоянии х. Для его момента инерции по теореме Гюйгенса-Штейнера можно написать

(П 5.1)

а для момента инерции всего цилиндра

(П 5.2)

Первое слагаемое в правой части формально совпадает с выражением для момента инерции однородного бесконечно тонкого стержня.

Следовательно,

(П 5.3)

Момент I_C инерции относительно поперечной геометрической оси, проходящей через центр масс цилиндра, можно найти по формуле (П 5.3), если цилиндр разделить на два цилиндра с высотой /2 и массами m`/2. Тогда получим

(П 5.3)

момент инерции всей системы можно вычислить по формуле

(П 5.3)

или

(П 5.3)