Эконометрика 11

Оглавление

Лабораторный практикум по парной регрессии и корреляции 1

РЕШЕНИЕ ЗАДАЧИ 5

ТЕМА 2 Отбор факторов при построении множественной регрессии 14

Вопрос 3: «Мультиколлинеарность». 21

РЕШЕНИЕ ТИПОВОЙ ЗАДАЧИ 22

Решение задач с помощью MS Excel 30

ТЕМА 3 Регрессионные модели с переменной структурой 34

Вопрос 1. «Фиктивные переменные во множественной регрессии». 34

Вопрос 2. Предпосылки метода наименьших квадратов 39

Вопрос 3. «Гетероскедатистичность» 43

РАЗДЕЛ 3 44

Лекция 6: «ХАРАКТЕРИСТИКИ ВРЕМЕННЫХ РЯДОВ» 44

Вопрос 1: «ОСНОВНЫЕ ЭЛЕМЕНТЫ ВРЕМЕННОГО РЯДА» 44

Вопрос 2: «АВТОКОРРЕЛЯЦИЯ УРОВНЕЙ ВРЕМЕННОГО РЯДА И ВЫЯВЛЕНИЕ ЕГО СТРУКТУРЫ» 45

Вопрос 3: «Моделирование тенденции временного ряда» 52

Вопрос 4: «Моделирование сезонных и циклических колебаний» 52

Вопрос 5: «Моделирование тенденции временного ряда при наличии структурных изменений». 57

Лабораторный практикум по парной регрессии и корреляции

Парная (простая) линейная регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной рассматривается как функция одной независимой (объясняющей) переменной x , т.е. это модель вида:

,

где: y – зависимая переменная (результативный признак);

х – независимая, объясняющая переменная (признак-фактор)

Так же y называют результативным признаком, а x признаком-фактором. Знак «^» означает, что между переменными x и y нет строгой функциональной зависимости.

Практически в каждом отдельном случае величина y складывается из двух слагаемых:

где y – фактическое значение результативного признака; – теоретическое значение результативного признака, найденное исходя из уравнения регрессии; – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии. Случайная величина называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.

Различают линейные и нелинейные регрессии.

Линейная регрессия: y=a+b*x+ε.

Нелинейные регрессии делятся на два класса: регрессия, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессия, нелинейные по оцениваемым параметрам.

Регрессии, нелинейные по объясняющим переменным:

• Полиномы разных степеней y=a+b₁*x+b₂*x²+b₃*x³+ε

• Равносторонняя гипербола

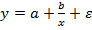
Регрессии, нелинейные по оцениваемым параметрам:

Степенная y=a*x^b*ε

Показательная y=a*b^x*ε

Экспоненциальная y=e^a+b*x*ε

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квардатов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических минимальна, т.е.

Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b:

Можно воспользоваться готовыми формулами, которые вытекают из этой системы:

Ковариация – числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий. Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r_xy для линейной регрессии (

И индекс корреляции p_xy - для нелинейной регрессии

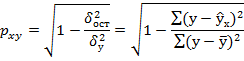
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.

Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:

Допустимый предел значений - не более 8-10%.

Средний коэффициент эластичности показывает, на сколько процентов в средней по совокупности изменится результат у от свой средней величины при изменении фактора х на 1% от своего среднего значения:

После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Оценка значимости уравнения регрессии в целом производится на основе F -критерия Фишера, которому предшествует дисперсионный анализ.

Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной y от среднего значения раскладывается на две части – «объясненную» и «необъясненную»

Где:

Схема дисперсионного анализа имеет вид, представленный в таблице (n – число наблюдений, m – число параметров при переменной x)

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Дисперсия на одну степень свободы
Общая
Факторная		m
Остаточная

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду (степени свободы – это числа, показывающие количество элементов варьирования, которые могут принимать произвольные значения, не изменяющие заданных характеристик). Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F -критерия Фишера (коэффициент (индекс) детерминации R²)

Коэффициент детерминации – квадрат коэффициента или индекса корреляции.

F-тест( F-критерий Фишера – оценивание качества уравнения регрессии – состоит в проверке гипотезы Н₀ о статистической значимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера F_факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

где:

n – число единиц совокупности;

m – число параметров при переменных х.

F_табл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.

Если F_табл < F_факт, то Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если F_табл > F_факт , то гипотеза Н₀ не отклоняется и признается статистическая значимость, ненадежность уравнения регрессии.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитывается t-критерий Стьюдента и доверительные интервалы каждой из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка знамчимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:

Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

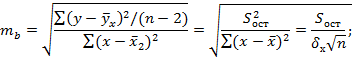
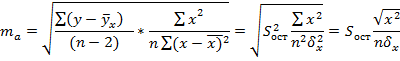
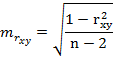
Домашнее задание

Сравнивая фактическое и критическое (табличное) значения t-статистики – t_табл и t_факт – принимаем или отвергаем гипотезу Н₀.

Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством

Если tтабл < tфакт, то Н₀ отклоняется, т.е. a,b и признается случайная природа формирования a,b, или

Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:

Формулы для расчета доверительных интервалов имеют следующий вид:

Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.

Прогнозное значение y_p определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения х_р . Вычисляется средняя стандартная ошибка прогноза

где

и строится доверительный интервал прогноза: