Контрольные вопросы

1. Объяснить работу принципиальной схемы заряжания и разряжания конденсатора.

2. Записать закон изменения заряда на пластинах конденсатора при разрядке.

3. Как связана сила тока разрядки конденсатора с зарядом на его пластинах?

4. Каков закон убывания силы тока во времени при разрядке конденсатора

5. Что такое время релаксации и как оно связано с параметрами электрического контура?

6. Как графически определить время релаксации?

7. Когда при изучении релаксационных процессов можно использовать измерительные приборы постоянного тока?

8. Как по кривой зависимости силы тока от времени при разрядке конденсатора определить величину заряда конденсатора?

9. Где используется инерционность процесса зарядки-разрядки конденсатора?

Примеры контрольных задач по теории лабораторной работы

Задача 1. Конденсатор емкостью 1 мкФ был заряжен при напряжении н его обкладках, равном 10 В. Определить время, в течение которого заряд конденсатора уменьшился вдвое, если время релаксации 20 с.

Задача 2. Через 14 с заряд конденсатора при разряде на сопротивление 1 МОм уменьшился вдвое. Определить время, за которое заряд конденсатора уменьшился в e раз.

Задача 3. График функции от времени разрядки конденсатора есть прямая, составляющая угол 10⁰ к оси времени. Чему равно время релаксации конденсатора? Во сколько раз уменьшится сила тока, текущего через сопротивление, через 2 с после начала процесса разрядки на это сопротивление?

Задача 4. Конденсатор емкостью 1 мкФ разряжается а) на сопротивление 2 МОм; б) на сопротивление 1 МОм. Найти отношение сил токов, текущих через сопротивления, через 2 с после начала разрядки конденсатора.

Лабораторная работа №6

ИЗУЧЕНИЕ ПОЛНОГО КОНТУРА ПРИ ПОМОЩИ «КОБРА-3».

6.1. Цель работы

Исследовать зависимость силы тока от частоты в последовательном контуре переменного тока. Определить собственную частоту контура. Для заданной частоты переменного напряжения построить векторную диаграмму тока и напряжений.

6.2. Теоретическое введение

6.2.1. Дифференциальное уравнение вынужденных электрических колебаний.

П усть в электрический контур, содержащий последовательно соединенные индуктивность L, емкость С и резистор R, подается внешнее переменное напряжение U=U₀cosωt, изменяющееся с циклической частотой ω (рис.1):

Рис.1

В любой момент времени для замкнутого контура должен выполняться второй закон Кирхгофа:

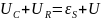(1)

Здесь U_C – падение напряжения на конденсаторе, U_R – падение напряжения на резисторе, ε_S – ЭДС самоиндукции и U – внешнее напряжение. Но:

; ;

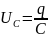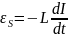
Следовательно, (1) можно представить в виде:

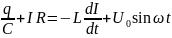(2)

Дифференцируя (2) по времени и учитывая, что 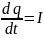, получим дифференциальное уравнение вынужденных электрических колебаний в последовательном электрическом контуре:

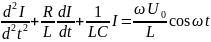(3)

Уравнение (3) есть неоднородное дифференциальное уравнение второго порядка относительно силы тока I.

Ясно, что вынужденные колебания тока имеют ту же частоту ω, что и внешнее напряжение. Поэтому решение уравнения (3) можно представить в виде:

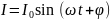, (4)

где I₀ (амплитуда тока) и φ (начальная фаза) пока не известны.