Контрольные вопросы
Что такое магнитная индукция? Как определить направление вектора ?
Записать закон Ампера. Как определить направление силы Ампера?
Что такое магнитный момент контура с током? Как направлен вектор магнитного момента контура?
Какое магнитное поле является однородным? Как выглядят линии магнитной индукции однородного магнитного поля?
Как рассчитать величину вращающего момента, действующего на рамку с током в магнитном поле?
Примеры контрольных задач по теории лабораторной работы
З
адача
1. В каком
направлении должен протекать ток в
соленоиде, чтобы наблюдать указанное
на рис.5 его взаимодействие с магнитной
стрелкой?
Задача 2. Какой силы ток должен проходить по прямому проводнику длиной 8 см, помещенному в однородное магнитное поле с индукцией 0,01 Тл, чтобы поле действовало на него с максимальной силой 0,002 Н? На какой угол необходимо повернуть проводник к линиям магнитной индукции, чтобы сила уменьшилась в 3 раза?
Задача 3. Виток радиусом 10 см расположен в плоскости магнитного меридиана. Какой вращающий момент действует на виток, если по нему течет ток силой 4 А? Горизонтальная составляющая магнитной индукции поля Земли равна 2⋅10-5Тл.
Задача 4. В однородном магнитном поле, индукция которого 1 Тл, помещена плоская катушка, состоящая из 100 витков радиусом 10 см, плоскость которой составляет угол α=600 с направлением магнитного поля. По катушке течет ток силой 10 А. определить вращающий момент, действующий на катушку.
Лабораторная работа №5
Изучение релаксационного процесса разрядки
конденсатора.
5.1. Цель работы
Исследование зависимости от времени силы тока на конденсаторе при его разрядке через активное сопротивление; определение времени релаксации.
5.2. Теоретическое введение
Пусть в некоторый момент времени обкладки заряженного конденсатора соединяются проводником с сопротивлением R, например, переводится ключ из положения 1 в положение 2 в схеме, изображенной на рис.1.
Рис.1. Принципиальная электрическая схема для изучения процесса разрядки конденсатора.
Считая ток I положительным, когда он течет от положительной обкладки конденсатора, запишем:
;
;
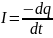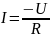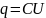(1)
где I, q, U – мгновенные значения силы тока, заряда обкладки конденсатора и разности потенциалов между обкладками; C – электроемкость конденсатора, R – сопротивление проводника. Знак «минус» в формуле (1) означает уменьшение заряда конденсатора при протекании положительного тока.
Исключая из уравнений (1) силу тока и напряжение, получим:
(2)
После разделения переменных имеем:
(3)
Проинтегрируем (3):
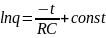(4)
Постоянную интегрирования найдем из начальных условий: при t=0 q=q0 (начальное значение заряда конденсатора).
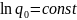(5)
Возвращаясь к (4), получаем
,
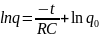или
;
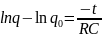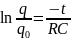(6)
После потенцирования имеем:
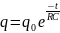7)
Следовательно, заряд конденсатора уменьшается со временем по экспоненциальному закону.
Введем
обозначение:
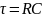(8).
Тогда
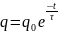(9),
где τ – время релаксации. Ясно, что время релаксации есть время, за которое заряд конденсатора уменьшается в e раз.
Дифференцируя формулу (9) по времени, находим закон изменения силы тока во времени:
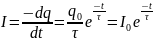(10)
где
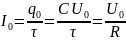начальное значение силы тока, где
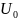– начальное значение напряжения на
конденсаторе.
Разделив формально уравнение (10) на I и выполняя операцию логарифмирования, получим:
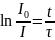
(11)
На
рис.2 показана линейная зависимость
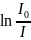от времени разрядки конденсатора t.
Рис.2
По углу α можно определить время релаксации, как
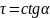(12).
Приведенные решения (9) и (10) получены в предположениях, что мгновенное значение силы тока одно и то же во всех поперечных сечениях проводника, соединяющего обкладки конденсатора, а мгновенное значение напряженности электрического поля такое же как и в электростатике при том же заряде на обкладках конденсатора. Токи и поля, удовлетворяющие этим условиям, называются квазистационарными. Квазистационарность тока нарушается при очень быстрых изменениях тока. Однако во многих практически важных случаях отклонение от квазистационарности несущественно.
Инерционность процесса разрядки конденсатора (при зарядке процесс аналогичен!) лежит в основе их широкого использования, в частности, в схемах преобразования переменного тока в постоянный, разделения постоянной и быстропеременной составляющих тока, подавления помех и т.п.
Вместе с тем, наличие емкости между различными проводниками, входящими в состав электронных приборов (диодов, транзисторов, микросхем на их основе), ограничивает их быстродействие. Для увеличения быстродействия цифровой схемы (например, микропроцессора) необходимо уменьшать длительность импульсов тока и напряжения, которые должна «обрабатывать» схема. Однако продолжительность импульсов не может быть меньше постоянной времени , поскольку на очень короткие импульсы схема не будет успевать реагировать.