Управление и оптимизация / Babenishev - Metodi optimizatsii 2017

ФБГОУ ВО СИБИРСКАЯ ПОЖАРНО-СПАСАТЕЛЬНАЯ АКАДЕМИЯ ГПС МЧС РОССИИ

С.В. БАБЕНЫШЕВ Е.Н. МАТЕРОВ

МЕТОДЫ

ОПТИМИЗАЦИИ

УЧЕБНОЕ ПОСОБИЕ

ЖЕЛЕЗНОГОРСК

2017

2

ФБГОУ ВО СИБИРСКАЯ ПОЖАРНО-СПАСАТЕЛЬНАЯ АКАДЕМИЯ ГПС МЧС РОССИИ

С.В. БАБЕНЫШЕВ, Е.Н. МАТЕРОВ

МЕТОДЫ ОПТИМИЗАЦИИ

УЧЕБНОЕ ПОСОБИЕ

ЖЕЛЕЗНОГОРСК

2017

3

УДК 517.97, 519.85

ББК 22.161.8 Б 12

Р е ц е н з е н ты :

канд. физ.-мат. наук А.В. Кротов канд. техн. наук М.И. Антипин

Бабенышев С.В., Матеров Е.Н.

Б12 Методы оптимизации: Учебное пособие для курсантов, студентов

ислушателей/ С.В. Бабенышев, Матеров Е.Н. – Железногорск: ФБГОУ ВО Сибирская пожарно-спасательная академия ГПС МЧС России, 2017.

– 122 с.: ил.

Настоящее учебное пособие предназначено для обучения курсантов, студентов и слушателей, обучающихся в ФБГОУ ВО Сибирская пожарно-спасательная академия ГПС МЧС России в соответствии с федеральным государственным образовательным стандартом высшего образования.

В пособии приведены необходимые теоретические сведения и примеры решения задач по дисциплине «Методы оптимизации», для обучения по очной, заочной и дистанционной формам обучения. Изложение материала ведется с упором на решение практических задач. В пособии используются примеры, иллюстрирующие применения, связанные с задачами МЧС России.

УДК 517.97, 519.85

ББК 22.161.8

Учебное издание

Бабенышев Сергей Валерьевич, Матеров Евгений Николаевич

МЕТОДЫ ОПТИМИЗАЦИИ

© ФГБОУ ВО Сибирская пожарноспасательная академия, 2017

4

5

ВВЕДЕНИЕ

«Методы оптимизации» – это математическая дисциплина, изучающая общие методы получения оптимальных решений в задачах, возникающих в естественных науках, экономике и инженерных приложениях. Оптимальное решение задачи ищется относительно заданной функции – целевого критерия, каким может быть, например, наименьший расход материалов, наименьшая стоимость производства, наименьшая дальность перевозки, наибольшая по стоимости загрузка транспортного средства, минимум ошибки и т.п. Дисциплина «Методы оптимизации» в значительной степени связана с рядом родственных разделов и дисциплин, таких как «Поддержка методов принятия решений», «Исследование операций» и «Теория оптимального управления».

Методы, изучаемые в «Методах оптимизации», применяются в системах поддержки логистики и организации производства, на транспорте, при программировании и проектировании промышленных и технологических установок и бытовых приборов.

Целью данного пособия является изложение идей и методов дисциплины «Методы оптимизации» на уровне достаточном для усвоения материала обучающимися без специального математического образования. Для иллюстрации теоретического материала широко используются рисунки и подробный разбор решения примеров.

Структурно пособие разделено на три раздела: «Вариационное исчисление и оптимальное управление», «Условная и безусловная оптимизация» и «Линейное программирование». Каждый раздел делится на логически взаимосвязанные темы, хотя существуют идеи и подходы, общие для тем из различных разделов. Так, например, в Теме 1 «Элементы вариационного исчисления» применяются подходы аналогичные используемым в Теме 5 «Методы безусловной оптимизации», а идея двойственности явно или неявно присутствует почти во всех разделах «Методов оптимизации». Далее, каждая тема представлена серией рассматриваемых вопросов, которые могут быть взяты за основу для формирования учебных вопросов для лекционных или практических занятий. Внутри каждой темы используется отдельная нумерация рисунков, формул и примеров.

6

РАЗДЕЛ 1. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ

Тема 1. Элементы вариационного исчисления

Вопрос 1. Экстремальные задачи и методы их решения

Предмет вариационного исчисления рассмотрим на примере двух истори-

ческих задач: задачи о брахистохроне и задачи о наибольшей площади.

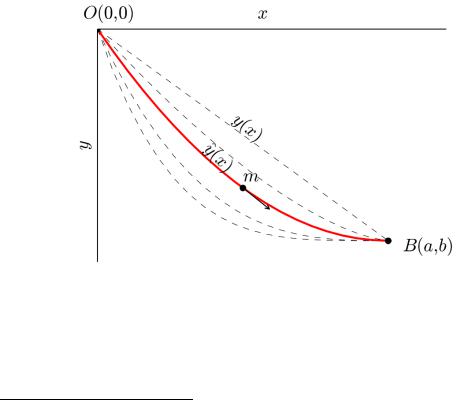
Задача о брахистохроне1. Даны две точки A и B, лежащие в вертикальной плоскости. Какова траектория материальной точки, движущейся только под действием силы тяжести, которая начинает двигаться из начальной точки A и достигает конечной точки B за кратчайшее время?

Задача о брахистохроне была предложена научному сообществу Иоганном Кеплером в 1696 году. Свои решения прислали или опубликовали: Исаак Ньютон, Готлиб Лейбниц, Гийом Лопиталь, Якоб Бернулли, Эренфрид Чирнхаус.

Дадим вариационную формулировку этой задачи (см. рис. 1).

Пусть A = O(0,0) – начальная точка совпадает с началом координат, конечная – B = B(a, b). Пусть y = y(x) – какая-то траектория движения материальной точки. Выразим скорость движения ν(x) материальной точки с массой m двумя способами и приравняем выражения между собой.

Рис. 1. Иллюстрация к задаче о брахистохроне.

1) Из закона сохранения энергии

1 Брахистохрона (от греч. βραχιστοζ (брахистос) – кратчайший, χρονοζ (хронос) – время) – кривая наискорей-

шего спуска.

7

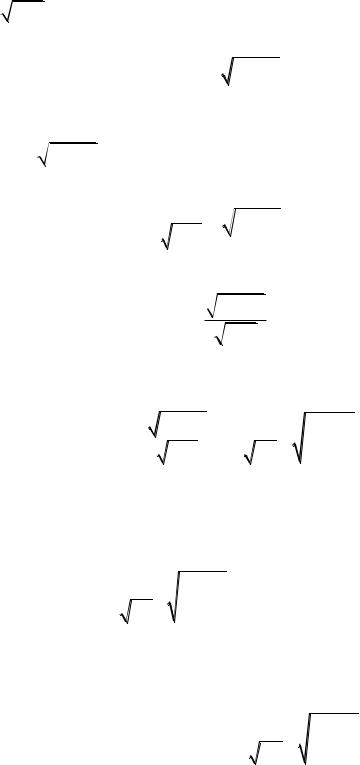
получаем v 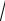2gy .

2) С другой стороны:

где dl – элемент дуги кривой, который можно расписать, при явном задании функции, как dl 1 y 2 dx .

Приравнивая выражения для v, получаем:

или, разделяя переменные,

dt 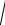1 y 2 dx.

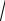2gy

Таким образом, общее время T прохождения точкой, движущейся по траектории (x, y(x)) при изменении параметра от 0 до a, равно

значение T(y).

В современной формулировке это записывается следующим образом:

Замечание. В формулировке задачи о брахистохроне используется сокращение inf (от лат. infimum – низший). Если в вариационной задаче требуется искать кривую, на которой достигается максимум, то вместо inf пишут sup (сокращение от лат. supremum – высший). В альтернативной постановке, argmin –

это сокращение от «аргумент минимума»

8

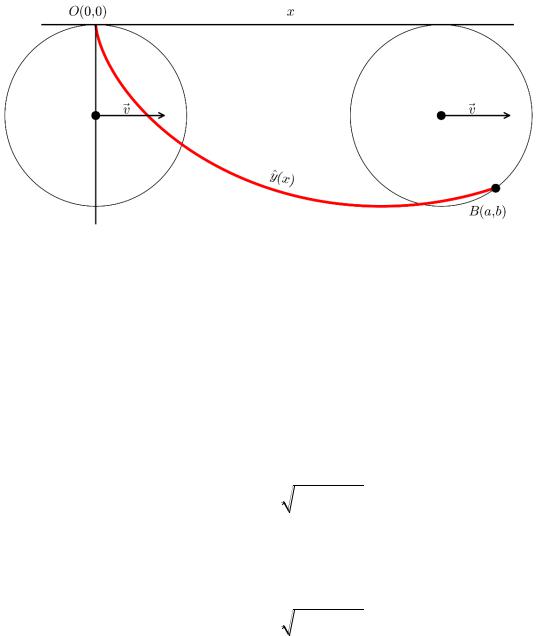
Решением задачи о брахистохроне является дуга вертикальной циклоиды с точкой возврата в точке А. Вспомним, что циклоида (рис. 2) – это плоская кривая, заданная траекторией движения точки, закрепленной на ободе движущегося колеса. Аналитически циклоиду можно задать с помощью пары параметрических уравнений:

x(t) r(t sin t),y(t) r(1 cost).

Рис. 2. Циклоида.

Брахистохроны применяют при проектировании трамплинов, аттракционов, технологических спусков и так далее.

Задача о наибольшей площади. Среди всех плоских кривых, имеющих данную длину l и оканчивающихся в точках A(a,0) и B(b,0) найти кривую y(x), ограничивающую вместе с отрезком [a, b] наибольшую площадь (рис. 3).

В современной формулировке:

или, в альтернативной записи,

Задачу о наибольшей площади еще называют изопериметрической задачей (задачей постоянного периметра) или задачей Дидоны, по мотивам известного исторического мифа об основании Карфагена его первой царицей – Дидоной.

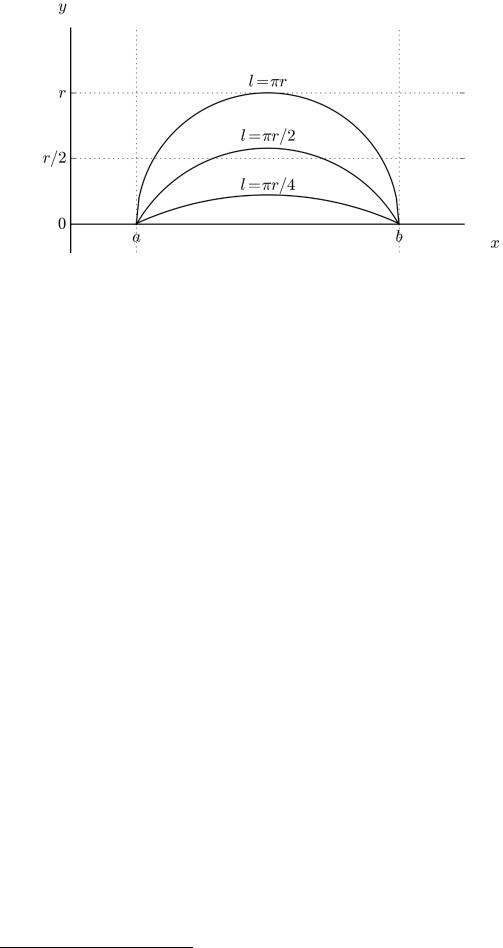
9

Рис. 3. Дуги окружности – решения задачи о наибольшей площади.

С методами вариационного исчисления познакомимся на примере реше-

ния простейшей задачи вариационного исчисления (ПЗВИ).

Простейшая задача классического вариационного исчисления.

Постановка задачи:

где f (x, y, y ) – функция от трех переменных, называемая интегрантом; extr2 – обозначает inf или sup;

отрезок a x b предполагается фиксированным и конечным;

выражение J ( y) ab f (x, y(x), y (x))dx называется функционалом.

Любой функционал, по существу, является функцией от функций, так как для любой подходящей функции однозначно определяет число – значение функционала на этой функции.

Вспомним, что на произвольном отрезке [a, b] выделяют следующие специальные множества функций, образующие линейные функциональные пространства (то есть множества функций, замкнутые относительно сложения и умножения на число):

C[a, b] – непрерывные функции;

C1[a, b] – непрерывно дифференцируемые или гладкие;

KC[a, b] – кусочно-непрерывные;

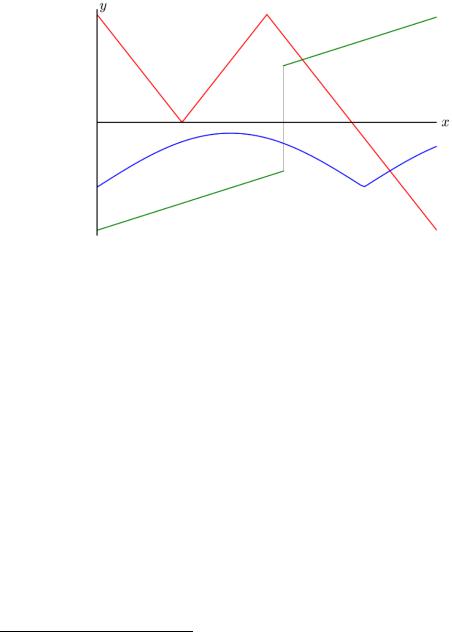
KC1[a, b] – кусочно-непрерывно дифференцируемые (см. рис. 5).

2 extr – от лат. extremum, обозначает экстремальное, то есть наибольшее или наименьшее значение.

10

Для запоминания этих обозначений удобно пользоваться следующими мнемоническими3 правилами:

1)С – сокращение от англ. “continuous”, непрерывный;

2)К – сокращение от «кусочно»;

3)верхний индекс показывает порядок производной, до которого, включительно, применимо указанная комбинация свойств.

Эти же соглашения обобщаются и на обозначения других классов функций, так, например, C2[a, b] обозначает класс дважды непрерывно дифференцируемых функций, то есть функций, имеющих непрерывные производные до второго порядка включительно.

Рис. 5. Кусочно-непрерывно дифференцируемая (кусочно гладкая) функция – это функция, которая сама является непрерывной и имеет производную, которая кусочно-непрерывна. На рисунке «зеленая» функция – кусочно-непрерывна, а «красная» и «синяя» – кусочно гладкие («изломы» на их графиках свидетельствуют о скачках их производных).

В ПЗВИ, экстремум функционала J ищется среди непрерывно дифференцируемых функций y C1[a, b], удовлетворяющих краевым условиям

y(x0 ) y0 , y(x1) y1 .

В общем случае, функции, удовлетворяющие ограничениям заданной вариационной задачи, называются допустимыми.

В пространствах C[a, b] и C1[a, b] будем рассматривать нормы4 || y ||C и

||y ||C1 , соответственно:

||y ||C: maxa x b | y(x) |

3Мнемоническое правило, здесь – правило, необязательно учитывающее реальное происхождение термина или сокращения, но удобное для запоминания.

4Норма функции, по сути, это функционал со специальными свойствами, такими как линейность и неравенство треугольника. Интегральные функционалы, такие как в постановке задачи ПЗВИ, уже являются линейными в силу свойства линейности интеграла.