Управление и оптимизация / Babenishev - Metodi optimizatsii 2017

имеет смысла, ввиду того, что, по части I, целевая функция является строго вогнутой, соответственно, глобальный максимум достигается в единственной точке.

III. Построим графическую иллюстрацию к задаче (Рис. 5).

Рис. 5

Ответ. Точка (4,0) является точкой наибольшего загрязнения.

Замечание. Решение задачи, разобранной в примере, возможно и чисто геометрическим способом. Необходимость привлекать алгоритмические методы возникает при рассмотрении тел более сложной формы или же при массовых расчетах, как например при расчетах на цифровых картах, где географические области часто задаются многоугольниками, не обязательно выпуклыми, каждый из которых может быть разрезан на треугольники.

72

Тема 5. Методы безусловной оптимизации

Вопрос 1. Постановка задачи безусловной оптимизации

В общем виде задача безусловной оптимизации формулируется так:

f (x) min, x n .

Не существует универсальных методов решения этой задачи. Обычно приходится подбирать подходящие методы в соответствии с видом целевой функции и искать локальный минимум, вместо глобального.

Рис 1. График функции класса С( 2 ) с областью «овражного типа».

При решении задачи f (x) min, x n , важное место занимает вопрос об условиях оптимальности. Выделяют два вида таких условий:

необходимые, т.е. условия, которым с необходимостью должна удовлетворять оптимальная точка;

достаточные, т.е. условия, выполнения которых достаточно для того, чтобы данная точка была оптимальной.

Важность условий оптимальности обусловлена тем, что такие условия для задачи f (x) min, x n :

1)составляют основу качественных методов;

2)используются при построении и обосновании численных методов;

3)в простых случаях, позволяют решить задачу.

Пример. Если известно, что минимум всюду определенной дифференцируемой функции существует, можно найти, исходя из необходимого условия, все стационарные точки и выбрать те в которой значение функции минимально.

74

Таким образом, в стационарной точке экстремальности и характер экстремальности точки прямо зависит от положительной (отрицательной) определенности матрицы Гессе, то есть от знака выражения hH f (x )h T , при произвольных при-

ращениях h .

Замечание. Рассмотренные необходимые и достаточные условия дают ос-

нову для построения методов локальной безусловной оптимизации, то есть методов поиска локальных максимумов и минимумов функции.

Вопросы для самоконтроля.

2.Чем отличаются необходимые и достаточные условия существования экстремума? Выполнение каких из них предпочтительней для нахождения экстремума?

3.Сформулируйте необходимое условие 1-го порядка.

4.Сформулируйте достаточное условие 2-го порядка.

5.Может ли быть в точке экстремум, если в этой точке не выполнено необходимое условие существования экстремума?

6.Может ли быть в точке экстремум, если в этой точке не выполнено достаточное условие существования экстремума?

7.Может ли быть в точке экстремум, если в этой точке выполнено необходимое условие, но не выполнено достаточное существования экстремума?

8.Почему рассмотренные необходимые и достаточные условия называются условиями 1-го и 2-го порядка?

75

Вопрос 2. Методы локальной безусловной оптимизации

Рассмотрим использование методов спуска для решения задач локальной безусловной оптимизации.

Общая схема методов спуска

Строится последовательность приближений

x 0 , x1, x 2 , , x N xlocmin

по правилу

x k 1 x k k h k ,

где

вектор h k направлен в сторону убывания целевой функции;

k 0 – параметр, регламентирующий длину шага h k ;

x 0 – начальное приближение, т.е. некоторая точка, выбираемая в окрестности локального минимума.

Одной из разновидностей методов спуска являются градиентные методы, которые относятся к методам первого порядка, поскольку используют при расчетах производные функции не выше первого порядка.

Градиентные методы

Градиентные методы являются частным случае методов спуска, в которых направление спуска всегда выбирается в направлении антиградиента.

Общая схема. Пусть f (x) C1( n )

направление спуска совпадает с антиградиентом, т.е. h k f (x k ) ;

k 0, k 0, , N ;

Варианты градиентного метода различаются между собой правилами выбора шага k . Далее рассмотрим два варианта:

Метод наискорейшего спуска.

Метод дробления шага.

76

Рис 2. Поведение «чистого» градиентного метода при минимизации функции «овражного» типа.

Метод наискорейшего спуска

Градиентный метод наискорейшего спуска в качестве длины шага k

использует величину, при которой величина функции f (x ) минимальна в направлении антиградиента ( f (x k ) ):

f (x k 1) f (x k k f (x k )) min f (x k f (x k )) .

Замечания.

1.Нахождение k сводится к задаче одномерной оптимизации.

2.Численная реализация требует множественных вычислений значения целевой функции.

Рис 3. Поведение метода наискорейшего спуска при минимизации «овражной» функции.

77

Метод дробления шага

Градиентный метод дробления шага в качестве длины шага использует величину k , которая удовлетворяет условию:

f(x k ) f (x k k f (x k )) 12 k f (x k ) 2 .

Вкачестве k последовательно проверяются значения:

, , 2 , 3 , 4 , ,

где 0 и (0,1) выбираются заранее (например, 10, 1/ 2 ).

Рис 4. Поведение метода дробления шага при минимизации «овражной» функции.

Метод Ньютона

Метод Ньютона относится к разряду методов второго порядка, поскольку используют производную функции второго порядка.

В методе Ньютона (методе касательных) в качестве k h k берется зна-

чение ( H 1(x k ) f (x k ) ), т.е.

x k 1 x k H 1(x k ) f (x k ) .

Замечания.

1.Метод Ньютона в целом эффективнее метода дробления шага.

2.Обращение матрицы является численно трудоемким.

3.На практике используются различные вариации метода Ньютона – ква-

зиньютоновские методы.

78

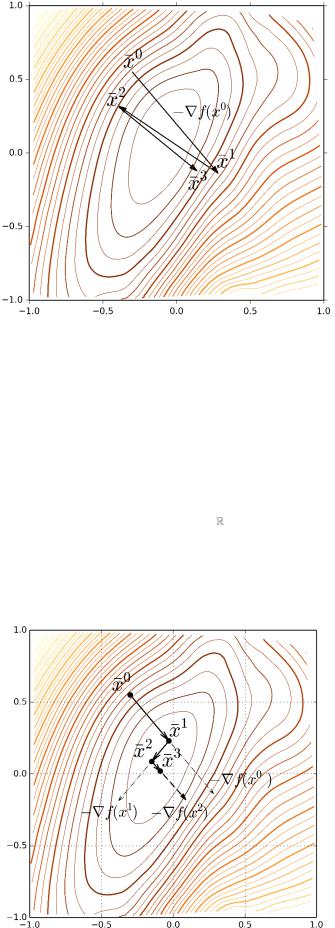
Рис 5. Поведение метода Ньютона при минимизации «овражной» функции.

Эвристические условия остановки итерационных методов

Будем использовать следующие условия остановки алгоритма поиска оптимума, основанные на абсолютной погрешности:

1)| x k 1 x k | 1 ;

2)| f (x k 1) f (x k ) | 2 ;

3)| f (x k 1) | 3 .

Замечания.

1.В условиях остановки 1) и 3) модуль обозначает длину вектора, в условии 2) – модуль числа.

2.Для остановки могут использоваться также комбинации любых двух или всех трех условий одновременно.

3.Условия остановки называются эвристическими, поскольку обладают тем свойством, что срабатывают в большинстве практических случаев, но не всегда. Для любого из этих условий можно привести пример не экстремальной точки, в окрестности которой условие срабатывает.

Условия остановки используются следующим образом.

1. До начала вычисления выбираются одно или несколько условий из

79

2. Если на k+1-шаге выполняются все из выбранных условий, то вычисления прекращаются и полагается

xlocmin x k 1 .

Вопросы для самоконтроля.

1.Запишите формула Тейлора для функции нескольких переменных (в разложении до 2-го порядка).

2.Какие условия остановки используются для прекращения поиска? Поясните их смысл.

3.Какие недостатки чистого градиентного метода вы можете указать?

4.Какие недостатки метода наикратчайшего спуска вы можете указать?

5. Почему рассмотренные условия остановки называются эвристическими? Можете ли вы описать ситуацию, когда они не срабатывают?

6. Верно ли что в среднем методы второго порядка сходятся быстрее чем методы второго порядка? Почему? Значит ли это, что они безусловно эффективнее?

7. Можете ли вы привести примеры функций, для которых градиентные методы эффективнее, чем метод Ньютона?

Покажем применение метода наискорейшего спуска на примере. В этом же примере для сравнения приведем также численный расчет точки минимума с помощью метода второго порядка – метода Ньютона.

Пример. Пусть даны целевая функция f (x, y) 4x2 4y2 6xy и начальная точка x 0 ( 2;1).

80

II. Используя метод Ньютона,

1)сделать 2 шага для вычисления минимума функции f(x, y);

2)отложить шаги и направления спуска на чертеже;

3)сделать выводы о последующих шагах и погрешностях.

Решение.

I. Метод наискорейшего спуска.

Основная формула:

x k 1 x k k f (x k ) ,

Общий вид градиента целевой функции:

f (x) ( f / x, f / y) (8x 6y,6x 8y) .

1) Шаг k=0.

f (x 0 ) (8 ( 2) 6 1;6 ( 2) 8 1) ( 10; 4) .

x 0 f (x 0 ) ( 2;1) ( 10; 4) ( 2 10 ;1 4 ) .

Решаем одномерную оптимальную задачу:

0 ( ) f (x 0 f (x 0 )) 4( 2 10 )2 4(1 4 )2 6( 2 10 )(1 4 ) min

В данном случае оптимальное решение можно найти из условия стационар-

ности ( ) 0:

0

( ) 8 ( 2 10 ) 10 8 (1 4 ) 4 60 (1 4 ) 24 ( 2 10 )

0

160 800 32 128 60 240 48 240

1408 116 0

0 116 / 1408 0,0823863636 0,08.