§7Знакочередующиеся ряды; ряд Лейбница; признак Лейбница; оценка суммы ряда Лейбница.

Пусть задана положительная числовая последовательность

Определения.

1. Числовой ряд называетсязнако-чередующимся рядом.

2. Рядом Лейбница называется знакочередующийся ряд, модули членов которого монотонно убывают

Теорема(признак сходимости Лейбница).

1)Ряд Лейбница расходится, если , исходится, , если ;

2) для сходящегося ряда Лейбница S=S_n+R_n имеют место

оценки сверху для суммы ряда и суммы его остатка

Док-во.

Если ряд расходится по «достаточному признаку расходимости».

Пусть . Четные частичные суммы ряда

Таким образом,

Остаток сходящегося ряда ряда Лейбница так же является рядом Лейбница. Модуль суммы остатка удовлетворяет неравенству, причем «знак» этой суммы равен «знаку» первого члена остатка –(-1)ⁿ⁺² .

Замечания.

1. Необходимый признак сходимости числовых рядов ()является для рада Лейбница достаточным признаком сходимости.

2) Из доказанной теоремы следует АЛГОРИТМ получения оценки суммы сходящегося ряда Лейбница с заданной погрешностью eps.

[I] Установливается сходимость ряда .

[II] Последовательно вычисляются и суммируются первые члены ряда до тех пор, пока выполняется неравенство |a_n|>eps.

[III] Записывается требуемая оценка суммы ряда в виде

Пример. Установить сходимость ряда и найти оценку его суммы с погрешностью не более 0.001.

[I]

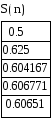
[II] S=1-0.5 +0.125 –0.020833+0.002604 – 2.604*10^-4 (<0.001 !!) +…

S₄=0.606771; |R₄| <0.0002604; R₄ <0



§8 Произвольные числовые ряды. Абсолютная и условная сходимость числового ряда.

Пусть задан произвольный числовой ряд ( вещественный или комплексный)

Составим из модулей членов ряда положительный числовой ряд

Теорема.

Если сходится положительный числовой ряд рядсходится.

Док-во.

(А) Докажем теорему сначала для произвольного вещественного ряда .

Рассмотроим два вспомогательных положительных ряда

Для этих рядов ряд из модулей оказываетсямажорирующим рядом и по теореме сравнения для положительных числовых рядов

Так как сходящиеся ряды можно почленно складывать(вычитать), то

(В) Доказательство теоремы для ряда с комплексными членами следует из (а) очевидного неравенства , (б) признака сравнения положительных рядов, в) доказанного утверждения (А) и (г) свойств сходящихся

рядов :

:

Определения.

1. Если сходится положительный числовой ряд, составленный из модулей членов ряда рядсходится и называетсяабсолютно сходящимся числовым рядом.

2. Если ряд расходится, а ряд сходится, говорят, что ряд сходится условно.

Например, ряд Лейбница СХ, но рядрасходится, поэтому рядсходитсяусловно.

Ряд же сходитсяабсолютно, так как ряд из модулей сходится по интегральному признаку сходимости.

Замечания.

1. При исследовании абсолютной сходимости числового ряда «работают» все признаки сходимости положительных рядов (например, пр. сравнения, интегральный признак, признаки Коши и Даламбера).

2. Признаки Коши и Даламбера можно сформулировать так

«Если существует конечный предел

отношения модулей последующего члена ряда к предыдущему или

арифметического значения корня степени n из модуля члена ряда,

ряд сходитсяабсолютно, если q<1, и расходится, если q>1 ».

3. Понятия «абсолютной» и «относительной» сходимости числового ряда относятся к двум рядам и