19

ГЛАВА «ЧИСЛОВЫЕ РЯДЫ» 1

§1 Числовой ряд: основные понятия. 1

§2 Свойства сходящихся числовых рядов. 3

§3 Положительные числовые ряды; признаки сравнения. 5

§4 Интегральный признак сходимости; оценка суммы ряда. 7

§5 Признаки Даламбера и Коши сходимости положительного ряда. 10

§6 Оценка суммы сходящегося положительного числового ряда. 11

§7Знакочередующиеся ряды; ряд Лейбница; признак Лейбница; оценка суммы ряда Лейбница. 14

§8 Произвольные числовые ряды. Абсолютная и условная сходимость числового ряда. 16

ГЛАВА «ЧИСЛОВЫЕ РЯДЫ»

§1 Числовой ряд: основные понятия.

Пусть задана числовая последовательность Определим другую числовая последовательность

Определение 1. Пара числовых последовательностей

называется числовым рядом, при этом последовательности (1) и(2) называют, соответственно, последовательностями членов ряда и частичных сумм ряда: a_n – n-ый (общий) член ряда; S_n- n-ая частичная сумма ряда.

Определение 2. Если существует конечный предел частичных сумм ряда , (1) говорят, что «ряд сходится»; (2) этот предел называют «суммой ряда» и пишут .

В противном случае говорят, что «ряд расходится» .

Примеры.

1. Арифметическая прогрессия с разностью «d» определяет расходящийся числовой ряд.

2. Геометрической прогрессией со знаменателем “q≠0” определяет ряд .

Исследуем его сходимость в зависимости от значения “q≠0”.

Таким образом, ряд

(3)

3. 

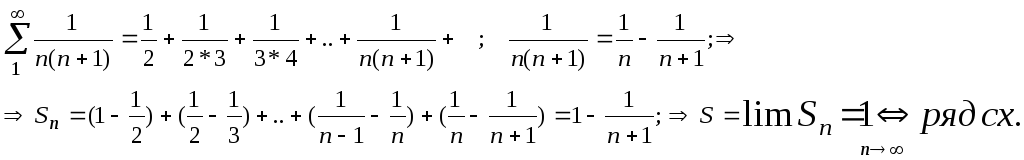
§2 Свойства сходящихся числовых рядов.

Из определения сходимости числового ряда и свойств пределов следуют очевидные свойства сходящихся рядов:

1. 

2. , .

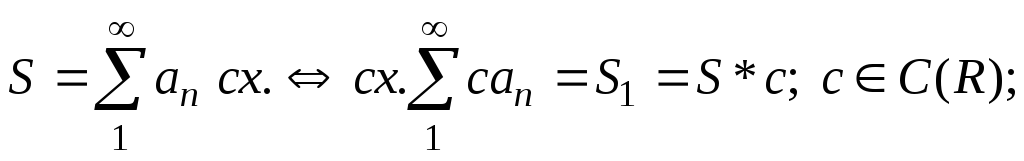
3. Так как частичная сумма ряда 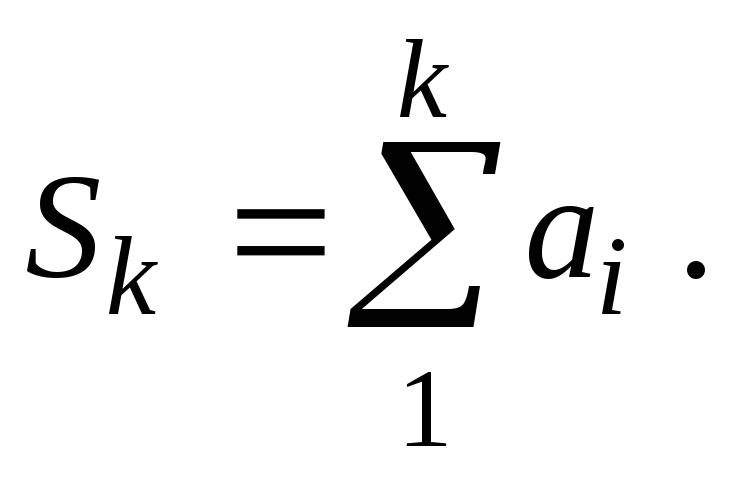- конечное число, ряд и «остаток ряда» сходятся и расходятся одновременно.

При «работе» с числовыми рядами приходится последовательно решать две задачи:

[1] исследование сходимости(расходимости) ряда;

[2] «оценка» суммы сходящегося ряда.

Первая задача решается либо «по определению», либо с помощью «признаков сходимости(расходимости» рядов – теорем, устанавливающих связь между сходи-мостью(расходимостью) ряда и свойствами членов ряда.

Примером такого признака является «достаточный признак расходимости » числового ряда.

Теорема (необходимый признак сходимости; достаточный признак расходимости).

(а) Если числовой ряд сходится, предел модуля его общего члена равен нулю;

(б) если предел модуля общего члена ряда не равен нулю, ряд расходится.

Док-во.

(а) Пусть ч.р. сходится

(б) докажем “методом от противного”. Пусть ??

Предположим, что ряд сх., тогда по доказанному (а) , что противоречит условиюпредположение не верно ряд расходится.

Замечание. Условие (а) является необходимым, но не достаточным для сходимости ряда: например,

Рассмотрим постановку задачи [2].

Пусть ч.р. сходится и S=. Запишем равенство

Из сходимости ряда, очевидно, следует сходимость и «остатка ряда» , причем сумма остаткаи

Таким образом

при «достаточно больших К» сумма сходящегося ряда сколь угодно «мало» отличается от его частичной суммы S_k , т.е. S_k является “приближенным значением” суммы ряда S.

Определение.

Интервал [a,b]; (b-a)≤εps называется «эпсилон-оценкой» суммы ряда, если

Замечание. Если для числового ряда удается оценить сверху модуль суммы остатка ряда , то «- оценка» суммы ряда имеет вид

,

причем левый конец интервала округляют«по недостатку», а правый – «по избытку», например,