
- •Уведемо до розгляду вектор-рядок коефіцієнтів прямої трудомісткості
- •11.Оптимізація міжгалузевого балансу
- •12.Математична форма критерію оптимальності
- •13. Моделювання цільової функції сприяння досягнення мети
- •14. Коригуюча функція
- •15.Локальний критерій
- •16.Задача розміщення торговельних точок
- •17.Задача оптимального використання парку будівельних машин
- •18.Транспортна задача з фіксованими доплатами
- •19.Методи розв’язування транспортної задачі з фіксованими доплатами
- •20.Виробничі функції та функції виробничих затрат
- •21.Взаємні задачі
17.Задача оптимального використання парку будівельних машин
 об’єкти
робіт
об’єкти
робіт
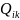 -
обсяг
робіт
-
обсяг
робіт
 -
вид
технологічного засобу
-
вид
технологічного засобу
 – ресурс
часу j-го
технологічного засобу
– ресурс
часу j-го
технологічного засобу
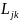 -
продуктивність
виконання робіт j-ою
машиною за одиницю часу
-
продуктивність
виконання робіт j-ою
машиною за одиницю часу
 -
приведені затрати на виконання
k-ої
роботи
j-им
технологічним засобом
-
приведені затрати на виконання
k-ої
роботи
j-им
технологічним засобом
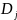 – витрати
на монтажні і демонтажні роботи j-го
технологічного засобу
– витрати
на монтажні і демонтажні роботи j-го
технологічного засобу
 -
обсяг
робіт
k-го
виду на
j-му
технологічному засобі на
i-му
об’єкті
-
обсяг
робіт
k-го
виду на
j-му
технологічному засобі на
i-му
об’єкті
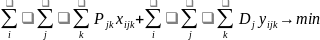
Де
 ;
;

 ;
;
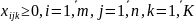
Транспортна задача з постійною складовою:
 ;
;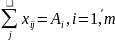
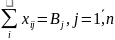 ;
;

18.Транспортна задача з фіксованими доплатами
Нехай
у пунктах ![]() виробляється
деякий однорідний продукт, причому
обсяг виробництва цього продукту в
пункті
виробляється
деякий однорідний продукт, причому
обсяг виробництва цього продукту в
пункті ![]() дорівнює
дорівнює ![]() одиниць,
одиниць, ![]() Зроблений
у пунктах виробництва продукт повинен
бути доставлений до пунктів
споживання
Зроблений
у пунктах виробництва продукт повинен
бути доставлений до пунктів
споживання ![]() причому
обсяг споживання в пункті
причому
обсяг споживання в пункті ![]() складає
складає ![]() одиниць
продукту. Вважається, що транспортування
готової продукції можливе з будь-якого
пункту виробництва в будь-який пункт
споживання і транспортні витрати, що
припадають на перевезення одиниці
продукту з пункту
в
пункт
одиниць
продукту. Вважається, що транспортування
готової продукції можливе з будь-якого
пункту виробництва в будь-який пункт
споживання і транспортні витрати, що
припадають на перевезення одиниці
продукту з пункту
в
пункт ![]() складають
складають ![]() грошових
одиниць. Задача полягає в організації
такого плану перевезень, при якому
сумарні транспортні витрати були б
мінімальними.
Формально
задача ставиться наступним чином.
Нехай
грошових
одиниць. Задача полягає в організації
такого плану перевезень, при якому
сумарні транспортні витрати були б
мінімальними.
Формально
задача ставиться наступним чином.
Нехай ![]() —
кількість продукту, що перевозиться з
пункту
в
пункт
—
кількість продукту, що перевозиться з
пункту
в
пункт ![]() Потрібно
визначити сукупність з
mn величин
Потрібно
визначити сукупність з
mn величин ![]() які
відповідають умовам:
які
відповідають умовам:
![]()
![]()
![]()
і
для яких лінійна форма ![]() набуває
найменшого значення.
Група обмежень (1)-(2)
пов'язана з тою обставиною, що обсяг
вивезеного з кожного пункту виробництва
продукту в точності дорівнює обсягу
виробленого в цьому пункті продукту, а
обсяг ввезеного в пункт споживання
продукту відповідає його потребі. За
цих обмежень необхідною і достатньою
умовою для розв'язності транспортної
задачі є виконання умови балансу:
набуває
найменшого значення.
Група обмежень (1)-(2)
пов'язана з тою обставиною, що обсяг
вивезеного з кожного пункту виробництва
продукту в точності дорівнює обсягу
виробленого в цьому пункті продукту, а
обсяг ввезеного в пункт споживання
продукту відповідає його потребі. За
цих обмежень необхідною і достатньою
умовою для розв'язності транспортної
задачі є виконання умови балансу:
![]()
Транспортна
задача з фіксованими доплатами. Вона
відрізняється від звичайної ТЗ тим, що
витрати на перевезення однорідного
вантажу з пункту Аі
в пункт
 визначають так:
визначають так:

де
 — витрати на перевезення одиниці
вантажу;
— витрати на перевезення одиниці
вантажу;
 — фіксована доплата за оренду
транспортних засобів. Із такими
припущеннями функція сумарних витрат
має розриви, що значно ускладнює її
мінімізацію. Тому вводять додаткові
бінарні змінні (що набувають лише двох
значень: 0
або 1),
які дають змогу усунути розриви функції
витрат і звести початкову задачу до
частково
цілочислової.
Так називають задачі, у яких умову
цілочисловості накладено лише на частину
змінних.
— фіксована доплата за оренду
транспортних засобів. Із такими
припущеннями функція сумарних витрат
має розриви, що значно ускладнює її
мінімізацію. Тому вводять додаткові
бінарні змінні (що набувають лише двох
значень: 0
або 1),
які дають змогу усунути розриви функції
витрат і звести початкову задачу до
частково
цілочислової.
Так називають задачі, у яких умову
цілочисловості накладено лише на частину
змінних.
19.Методи розв’язування транспортної задачі з фіксованими доплатами
Метод потенціалів
1.Як перше наближення до оптимального розв’язку вибирають будь-який початковий базисний розв’язок (побудований методом північно-західного кута, мінімального елемента чи іншим методом).
2.Визначають
потенціали так, щоб у кожній базисній
(ненульовій) клітині виконувалась умова
 =
0, тобто складають систему рівнянь Uі
+ Vj=
Сij
для всіх базисних клітин Хij
> 0. Зауважимо, що така система містить
т
+ п
- 1
рівнянь (за кількістю базисних клітин)
й т
+ п
невідомих, тому (як відомо з матричної
алгебри) має безліч розв’язків. Щоб
визначити хоча б один із них, одну зі
змінних довизначають, а всі інші знаходять
із зазначеної системи
3.За знайденими
потенціалами обчислюють відносні оцінки
небазисних (нульових) клітин. Якщо для
усіх цих клітин
> 0, то даний базисний розв’язок
оптимальний. Якщо ж існують небазисні
клітини, для яких
< 0, то цей розв’язок можна поліпшити,
тобто перейти до іншого базисного
розв’язку з меншою вартістю перевезень.
Як і в звичайному симплекс-методі, зміна
базису полягає в тому, щоб до базису
ввести змінну, яка має “найгіршу”
відносну оцінку, і вивести одну з поточних
базисних змінних. Очевидно, що до базису
вводять змінну з найменшою від’ємною
відносною оцінкою А,
<
0. Нехай це клітина (і0,,0).
Визначимо, яку з базисних клітин слід
вивести з базису. Для цього з клітин
транспортної таблиці утворимо цикл
(замкнений ланцюг) так, щоб він містив
клітину (і0,
j0)
(небазисну, нульову) і деякі базисні
клітини. Позначимо клітини циклу
так: небазисну — знаком “+”, а інші
(базисні) — знаком “-” чи “+”, але
так, щоб у кожному рядку та стовпці
транспортної таблиці була однакова
кількість різних знаків, що чергуються
між собою. Кожну наступну клітину для
позначення відповідним знаком вибирають
лише в тому самому рядку чи стовпці,
де вже є позначена. Починають і закінчують
цикл у небазисній клітині .Серед базисних
клітин, позначених знаком “-”, виберемо
найменше перевезення Ху
= хmin.
Збільшимо обсяг перевезень на
=
0, тобто складають систему рівнянь Uі
+ Vj=
Сij
для всіх базисних клітин Хij
> 0. Зауважимо, що така система містить
т
+ п
- 1
рівнянь (за кількістю базисних клітин)
й т
+ п
невідомих, тому (як відомо з матричної
алгебри) має безліч розв’язків. Щоб
визначити хоча б один із них, одну зі
змінних довизначають, а всі інші знаходять
із зазначеної системи
3.За знайденими
потенціалами обчислюють відносні оцінки
небазисних (нульових) клітин. Якщо для
усіх цих клітин
> 0, то даний базисний розв’язок
оптимальний. Якщо ж існують небазисні
клітини, для яких
< 0, то цей розв’язок можна поліпшити,
тобто перейти до іншого базисного
розв’язку з меншою вартістю перевезень.
Як і в звичайному симплекс-методі, зміна
базису полягає в тому, щоб до базису
ввести змінну, яка має “найгіршу”
відносну оцінку, і вивести одну з поточних
базисних змінних. Очевидно, що до базису
вводять змінну з найменшою від’ємною
відносною оцінкою А,
<
0. Нехай це клітина (і0,,0).
Визначимо, яку з базисних клітин слід
вивести з базису. Для цього з клітин
транспортної таблиці утворимо цикл
(замкнений ланцюг) так, щоб він містив
клітину (і0,
j0)
(небазисну, нульову) і деякі базисні
клітини. Позначимо клітини циклу
так: небазисну — знаком “+”, а інші
(базисні) — знаком “-” чи “+”, але
так, щоб у кожному рядку та стовпці
транспортної таблиці була однакова
кількість різних знаків, що чергуються
між собою. Кожну наступну клітину для
позначення відповідним знаком вибирають
лише в тому самому рядку чи стовпці,
де вже є позначена. Починають і закінчують
цикл у небазисній клітині .Серед базисних
клітин, позначених знаком “-”, виберемо
найменше перевезення Ху
= хmin.
Збільшимо обсяг перевезень на
 = хmin
у
клітинах, позначених знаком “+”, і
зменшимо на ту саму величину обсяг
перевезень у клітинах, позначених знаком
“-”. Після такого перерозподілу
вантажу одна з базисних клітин стане
вільною, тобто вийде з базису, а клітина
(і0,
j0)
ввійде до нього й міститиме перевезення
Xij
=
> 0.
4.Отриманий
новий базисний розв’язок перевіряють
на оптимальність. Процедура виконується
доти, доки для поточного базисного
розв’язку не виконається критерій
оптимальності.
= хmin
у
клітинах, позначених знаком “+”, і
зменшимо на ту саму величину обсяг
перевезень у клітинах, позначених знаком
“-”. Після такого перерозподілу
вантажу одна з базисних клітин стане
вільною, тобто вийде з базису, а клітина
(і0,
j0)
ввійде до нього й міститиме перевезення
Xij
=
> 0.
4.Отриманий
новий базисний розв’язок перевіряють
на оптимальність. Процедура виконується
доти, доки для поточного базисного
розв’язку не виконається критерій
оптимальності.
