14

Глава «Операционное исчисление» 1

§1 Несобственный интеграл по бесконечному промежутку. 1

§2 Оригинал, изображение, преобразование Лапласа. 3

§3Теорема Смещения 5

§4 Свертка оригиналов и ее изображение. 6

§5 Дифференцирование и интегрирование оригинала; изображение производной оригинала. 8

§6Таблица операционных соответствий 9

§7 Приложения операционного исчисления. 10

§8 ИДЗ « Операционное исчисление» 12

Глава «Операционное исчисление»

§1 Несобственный интеграл по бесконечному промежутку.

Пусть функция f интегрируема (кусочно непрерывна) на любом конечном промежутке [a;b]. Тогда интеграл с переменным верхним пределом определяет непрерывную функцию F: [a;∞)→R; F(x)=, для которой определен предел на бесконечности:

Определение. Если существует и конечен предел функции F на бесконечности, его называют несобственным интегралом по бесконечному промежутку , говорят, что этот несобственный интеграл сходится, и пишут:

.

В противном случае говорят, что несобственный интеграл расходится.

Примеры.

1. 

2. 

Из определения и свойств пределов следуют

Свойства несобственного интеграла.

1. Если известна первообразная F функции f и

(a) .

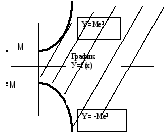
2. Для неотрицательной функции f (x)≥0 сходящийся несобственный интеграл равен площади «бесконечной» криволинейной трапеции.

3. Если - «признак сравнения» сходимости несобственных интегралов; .

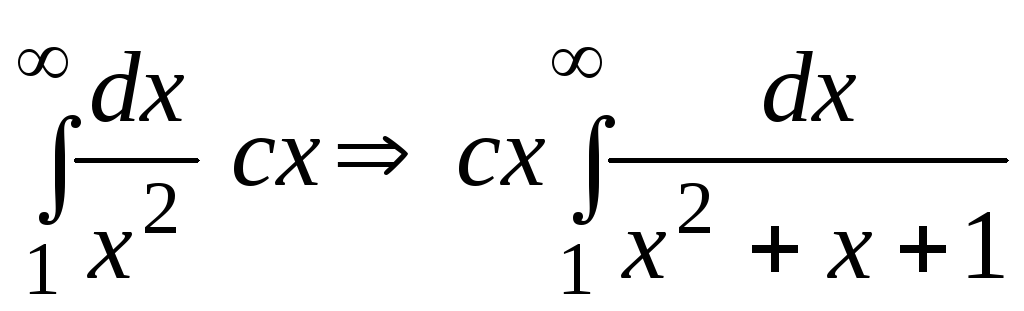4. Если сходится 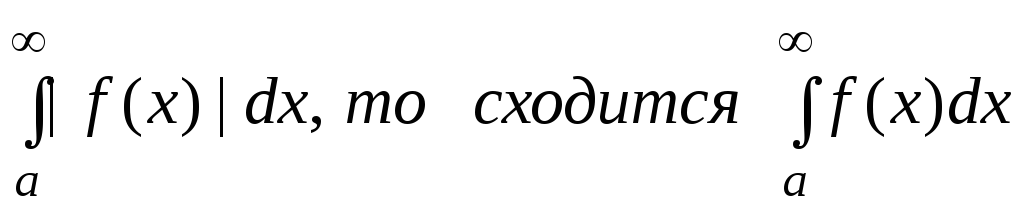- «признак абсолютной сходимости» несобственных интегралов:

5. Если f(x), g(x)>o и существует конечный предел отношения

сходятся и расходятся одновременно – «предельный признак сравнения» при исследовании сходимости несобственных интегралов.

Например, рассходится, так какирасходится.

§2 Оригинал, изображение, преобразование Лапласа.

«Функция≡отображение≡оператор» - однозначное соответствие между множествамиS и E_f.

Определение 1. Функция f:R®R, f(x) называется оригиналом fÎΘ, если :

1. "x<0 f(x)º0 ; 2) f интегрируема (кусочно-непрерывна) на любом конечном промежутке [a,b] 3) экспоненциально ограничена по модулю "xÎR $M,a_fÎR:úf(x)ú£M ּe^ax - f возрастает не быстрее некоторой экспоненты !!!

Пример. 1) 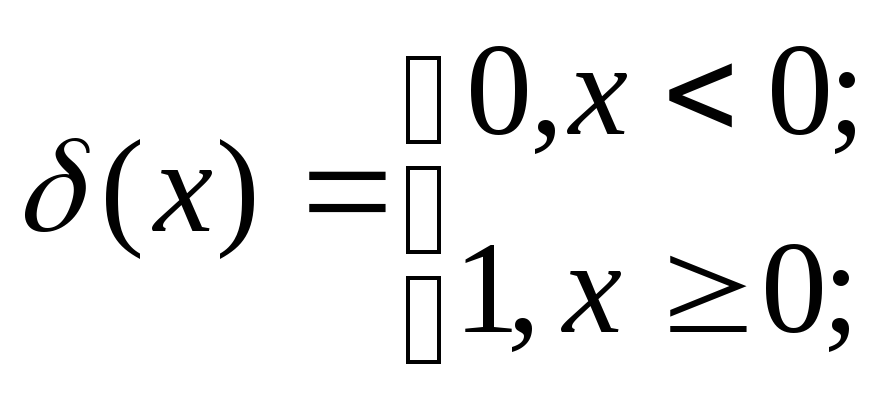единичная функция Хэвисайда  «отрицательный топор":

Изобразите графики : у1=x²d(x); у2=(x-1)²d(x); y3=(x-1)²d(x-1);

2) f2(x)=exp(5x)cos(2x)d(x)ÎQ: М₂=1;a₂=5;

3) f3(x)=exp(x²) ÏQ, т.к.exp(x²) возрастает БЫСТРЕЕ exp(ax) "aÎR

4) f4(x)=e^jxd(x)= (cos(x) + jsin(x))d(x) ÎQ, Ie^jxI= 1 Þ M=1; a₄=0;

5) Очевидно, что всякая функция, имеющая точки разрыва 2 рода не является оригиналом.

Пусть f - оригинал. Рассмотрим несобственный интеграл : :p€R.

Так как |f(x)|≤Me^αx  |f(x)e^-px| ≤Me^αx e^-px= Me^(α-p)x и несобственный интеграл от модуля

,

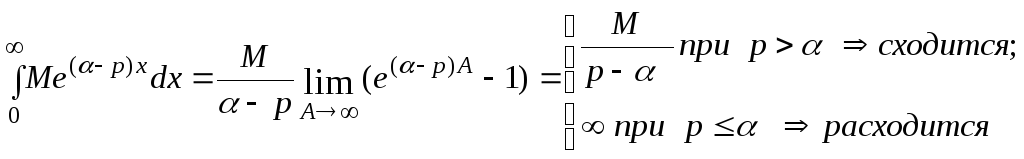несобственный интеграл сходится по признаку абсолютной сходимости дляp>α и определяет фунцию .

Определение 2. Если f - оригинал с показателем экспоненциального роста a , функция, опредлеляемая несобственным интегралом , называетсяизображением оригинала f.

Определение 3.

Однозначное соответствие L, которое функции-оригиналу f ставит в соответствие функцию-изображение оригинала, называется оператором Лапласа или (интегральным) преобразованием Лапласа: .

Замечание. В дальнейшем будем «по умолчанию» подразумевать, что fÎΘ  f(x)ּδ(x) и операционное соответствие L(f) будем записывать в виде .

Например,  .

ДЗ : доказать, что

Из определения L(f) и свойств интеграла следует свойство линейности преобразования Лапласа : L(c1f1(x)+c2f2(x)) = c1L(f1) + c2L(f2).

Например, L(2x-3e^2x)=2L(x)-3L(e^2x)=