8. Анализ чувствительности решения к изменению коэффициентов целевой функции

Анализ чувствительности полученного решения к изменению коэффициентов целевой функции предусматривает нахождение пределов изменений коэффициентов целевой функции Сj при условии неизменности полученного оптимального решения, т. е. Хi=const.

При исследовании на чувствительность решения к изменению коэффициентов целевой функции Сj прямой задачи удобно использовать решение двойственной задачи. Для двойственной задачи конечная симплекс-таблица в матричном виде может быть записана:

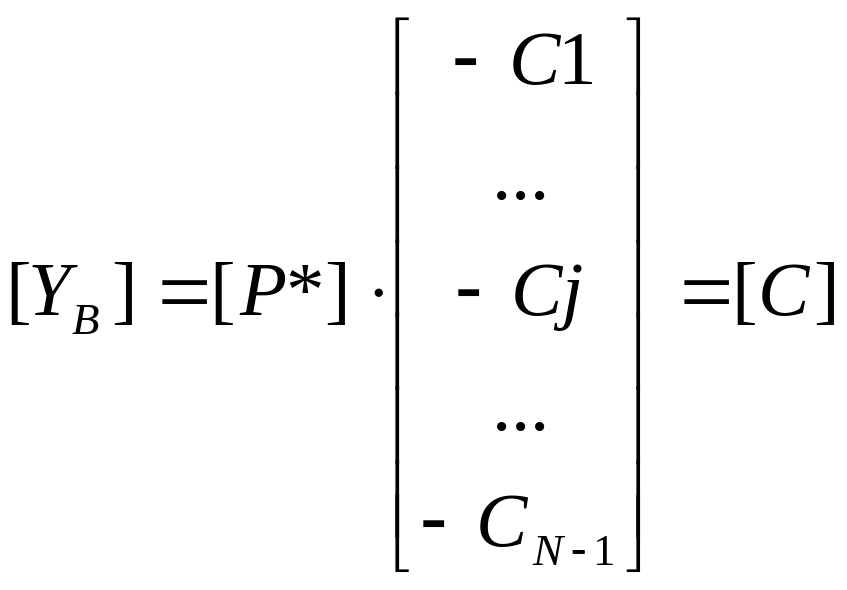
где [Y_B] – матрица-столбец базисных переменных конечной симплекс-таблицы двойственной задачи;

[P*] – матрица перехода базисных переменных конечной симплекс-таблицы двойственной задачи;

[-C1…-Cj…-C_N-1]^T – матрица-столбец исходных коэффициентов целевой функции прямой задачи (в двойственной задаче они играют роль правых частей ограничений);

[C] – матрица столбец конечных значений коэффициентов Сj двойственной задачи (для прямой задачи это конечное значение коэффициентов целевой функции).

Вектор устойчивости оптимального решения двойственной задачи к коэффициентам Сj равен:

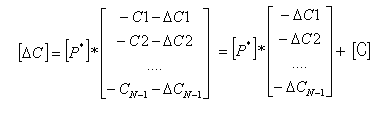
Вектор устойчивости коэффициентов Сj может быть записан через матрицу преобразования двойственной задачи [P*] в виде:

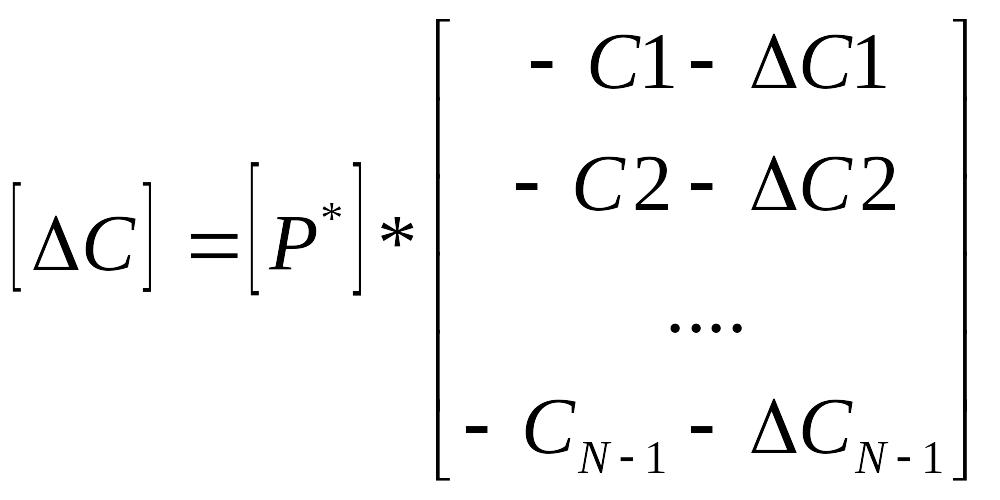
Анализ легко осуществлять отдельно для изменения каждого коэффициента Сj.

Матрица перехода для конечной симплекс-таблицы двойственной задачи имеет вид:

Условие неотрицательности компонент вектора [∆С] приводит к системе неравенств:

0 ,06 + ∆С2 - ∆С3  0;

-0,03 -∆С1+0,06+∆С2 - ∆С3  0;

0,03 + ∆С4  0;

0,06+∆С2 - ∆С3 – 0,06 - ∆С5 0;

0,03 + ∆С4-0,03 -∆С6  0.

Свободные члены неравенств совпадают со значениями коэффициентов последней столбца симплекс-таблицы прямой задачи.

Анализ этой системы легко осуществить отдельно для изменения каждого коэффициента Cj. Пределы изменения коэффициента Cj при переменной Xj, оказавшейся в последней симплекс – таблице прямой задачи в числе свободных, определяются непосредственно коэффициентом в строке целевой функции этой переменной.

Изменение коэффициентов при переменных, оказавшихся в числе базисных последней симплекс – таблицы, приводит к изменению целевой функции.

	-X2*	-X4*	-X3*	-Y4*	-Y5*	-Y6*	-Y7*	-Y8*	B
Y1*	-1	0	1	-1	0	0	0	0	0,03
X1*	-1	0	1	0	0	0	1	0	0,06
Y2*	0	-1	0	0	1	-1	0	0	0
Y3*	0	-1	0	0	1	0	0	1	0,03
X5*	-1	0	1	0	0	0	1	0	0,06
X6*	0	-1	0	0	0	0	0	0	0,03
Фmin	15	1	34	41	14	1	20	15	-0,97

1) Пусть ∆С10, ∆Сi=0, i=2..6, решая систему неравенств, получим:

∆С1 ≤ 0,03;

Изменение С1 в указанном пределе не приведет к изменению как оптимального решения, так и значения целевой функции (так как X1=0), значит изменение значении целевой функции будет ∆F_max=0.

2) Пусть ∆С20, ∆Сi=0, i=1,3..6, решая систему неравенств, получим:

∆С2  -0,03

∆С2  0

При изменении значения второго коэффициента целевой функции на ∆С2  -0,03, значение целевой функции изменится на ∆F_max  -0,45.

3) Пусть ∆С30, ∆Сi=0, i=1,2,4..6, решая систему неравенств, получим:

∆С3 ≤ 0,06;

∆С3 ≤ 0,03;

∆С3 ≤ 0

При изменении значения третьего коэффициента целевой функции на ∆С3 ≤ 0,06, значение целевой функции изменится на ∆F_max ≤ 2,04.

4) Пусть ∆С40, ∆Сi=0, i=1..3,5,6, решая систему неравенств, получим:

∆С4  -0,03.

∆С4  0

Изменение С4 в указанном пределе не приведет к изменению как оптимального решения, так и значения целевой функции (так как X4=0), значит изменение значение целевой функции будет ∆F_max=0.

5) Пусть ∆С50, ∆Сi=0, i=1..4,6, решая систему неравенств, получим:

∆С5 ≤ 0.

Изменение С5 в указанном пределе не приведет к изменению как оптимального решения, так и значения целевой функции (так как X5=0), значит изменение значение целевой функции будет ∆F_max=0.

6) Пусть ∆С60, ∆Сi=0, i=1..5, решая систему неравенств, получим:

∆С6 ≤ 0.

Изменение С6 в указанном пределе не приведет к изменению как оптимального решения, так и значения целевой функции (так как X6=0), значит изменение значение целевой функции будет ∆F_max=0.

Пусть ∆С10, ∆С30 ∆Сi=0, i=2,4,5,6, тогда получим систему неравенств:

∆С2  -0,03

∆С3 ≤ 0,06

Графически решение данной системы можно представить следующим образом:

Рисунок 3. Графическое решение системы

Изменение значений целевой функции будет происходить в пределах

∆F_max ≤ 2,04.

Возьмем, для примера, из найденной области точку с координатами ∆С2=0,04, ∆С3=0,01. Произведем решение задачи с новыми значениями С2 и С3 (0,1, 0,05).

Таблица 10. Конечная симплекс-таблица прямой задачи:

	-X1	-Y1	-Y2	-Y3	-X5	-X6	B
Х2	1	1	0	0	1	0	15
Х3	0	1	1	-1	1	1	34
X4	0	-1	0	1	-1	0	1
Y4	1	-1	-1	1	-1	-1	56
Y5	1	0	0	0	0	0	14
Y6	0	-1	-1	1	-1	-1	1
Y7	0	-1	-1	1	-1	-1	20
Y8	0	1	0	-1	1	0	15
Fmax	0,10	0	0,10	0,05	0,01	0,02	1,21

Значение рабочей точки не изменилось: Х2=15 и Х3=34.