5. Двойственная задача
Для любой задачи линейного программирования может быть поставлена в соответствие некоторая другая задача, которая называется двойственной по отношению к прямой.
В
двойственной задаче необходимо найти
значения переменных Yi*(i=1,M-1),
удовлетворяющие системе
,
где Yi*≥0(i=L+1,M-1),
Yi*(i=1,L)
обеспечивают минимальное значение
целевой функции
,
при этом Fmax = -Фmin. Таким образом, для
данной задачи двойственная ей будет
иметь вид.
Целевая функция:
Фmin=15Y1*+35Y2*+16Y3*+90Y4*+14Y5*+16Y6*+54Y7*+16Y8* → min
Ограничения:
Y1*+Y3*+Y7*≥0,0111;
Y1*+Y3*+Y4*+Y6*≥0,0286;
Y2*+Y4*+ Y7*≥0,0147;
Y2*+Y3*+Y8*≥0,04;
Y1≥0;
Y2≥0;
Yi*≥0, где i=1,9
Если исходную симплекс-таблицу прямой задачи представить в матричном виде:
А – матрица коэффициентов ограничений.
Исходную симплекс-таблицу двойственной задачи можно записать в виде:
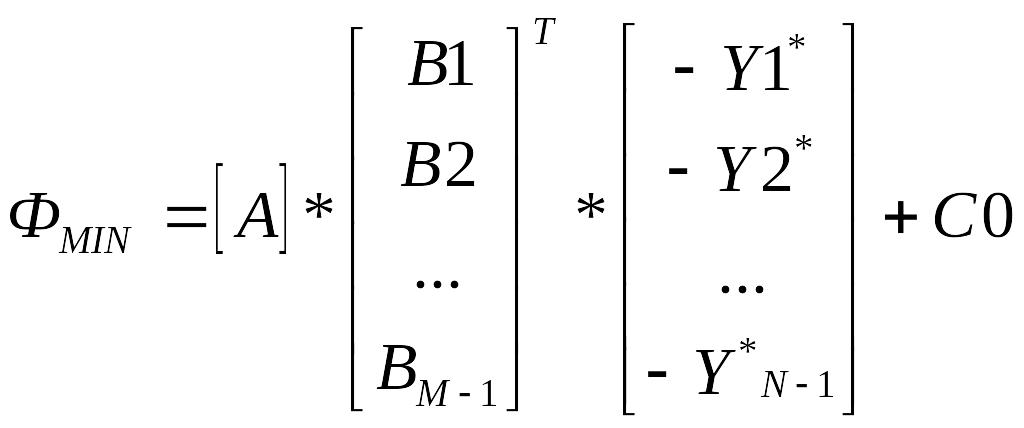
Отсюда
следует, что решение двойственной задачи
определяется из конечной симплекс-таблицы
прямой задачи и наоборот. Если формально
в качестве дополнительных переменных
для ограничений задачи использовать
переменные
,
а в качестве дополнительных переменных
для ограничений двойственной задачи –
переменные Хj*
,
то при решении двойственной задачи
симплекс-таблицу на любой итерации
симплекс-метода можно рассматривать
как транспонированную симплекс-таблицу
прямой задачи. При этом коэффициенты
строки целевой функции и столбца
свободных членов транспонируются без
изменения, а все остальные коэффициенты
таблицы одновременно с транспонированием
меняют знаки на противоположные.
Таблица 8. Исходная симплекс-таблица двойственной задачи:
|
-Y1* |
-Y2* |
-Y3* |
-Y4* |
-Y5* |
-Y6* |
-Y7* |
-Y8* |
B |
X1* |
-1 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
-0,01 |
X2* |
-1 |
0 |
-1 |
-1 |
0 |
-1 |
0 |
0 |
-0,03 |
X3* |
0 |
-1 |
0 |
-1 |
0 |
0 |
-1 |
0 |
-0,01 |
X4* |
0 |
-1 |
-1 |
0 |
0 |
0 |
0 |
-1 |
-0,04 |
X5* |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
X6* |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Фmin |
15 |
35 |
16 |
90 |
14 |
16 |
54 |
16 |
0 |
Таблица 9. Конечная симплекс-таблица двойственной задачи:
|
-X2* |
-X4* |
-X3* |
-Y4* |
-Y5* |
-Y6* |
-Y7* |
-Y8* |
B |
Y1* |
-1 |
0 |
1 |
-1 |
0 |
0 |
0 |
0 |
0,03 |
X1* |
-1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0,06 |
Y2* |
0 |
-1 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
Y3* |
0 |
-1 |
0 |
0 |
1 |
0 |
0 |
1 |
0,03 |
X5* |
-1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0,06 |
X6* |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0,03 |
Фmin |
15 |
1 |
34 |
41 |
14 |
1 |
20 |
15 |
-0,97 |
Решение двойственной задачи:
Y1* = 0,03;
Y2* = 0; Y3* = 0,03; Y4* = 0; Y5* = 0; Y6* = 0; Y7* = 0; Y8* = 0;
Значение целевой функции для двойственной задачи: Фmin= - 0,97.