ПРОГРАММИРОВАНИЕ ЗАДАЧ в СИСТЕМЕ MATH CAD

Операционная система WINDOWS, MS OFFICE, трансляторы

Лабораторная работа № 2.1 (C:\USER\GROUP\NOF\lab1.mcad)

РЕШЕние СИСТЕМ линейных АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

МЕТОДОМ ОБРАТНОЙ МАТРИЦЫ

2.1.1. Цель работы. Получение практических навыков алгоритмизации и программирования алгоритма решения линейных алгебраических уравнений методом обратной матрицы.

2.2.2. Справочный материал. Запишем систему линейно-независимых алгебраических уравнений, определитель которой не равен нулю, в следующем виде:

A₁₁X₁ + A₁₂X₂ + … + A_1NX_N = F₁

A₂₁X₁ + A₂₂X₂ + … + A_2NX_N = F₂ (2.1.1)

……………………………………………

A_N1X₁ + A_N2X₂ +… + A_NNX_N = F_N

В том случае, если система уравнений (2.1.1) является линейно-зависимой, определяется ранг матрицы (максимальное число линейно-независимых уравнений), линейно-зависимые уравнения исключаются, а полученная система линейно-независимых алгебраических уравнений решается методом обратной матрицы.

Систему линейных уравнений (2.2.1) запишем в векторном виде:

AX = F , (2.1.2)

где матрица А и вектор-столбцы Х и F имеют следующий вид:

Систему алгебраических уравнений (2.1.2), записанную в векторном виде слева, умножим на обратную матрицу A

A^-1AX = AF, поскольку A^-1A =E,

т. е. равно единичной матрице, то решение системы в векторном виде запишется следующим образом:

X = A^-1F . (2.1.3)

2.1.3. Пример. Решить методом обратной матрицы следующую систему уравнений:

2Х₁ + 3X₂ – 4X₃ = 6;

5X₁ – 2X₂ – 3X₃ = 2; ( 2.1.4 )

3X₁ + 2X₂ + 3X₃ =3.

Выпишем значения матричных элементов для матрицы А и вектор-столбцов X и F:

; ; .

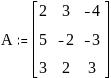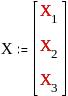Программа вычисления корней системы уравнений (2.1.4) методом обратной матрицы, записанная в системе MATH CAD, имеет следующей вид:

_.

Далее, проверим равно ли произведение обратной матрицы на матрицу А единичной матрице ( не будет равно в том случае, когда определитель матрицы А равен нулю или близок к нему). Для этого набиваем команды: ”А(-1)*А =“ , в результате имеем следующую запись:

.

Теперь по формуле (2.1.3) вычислим корни исходной системы уравнений (2.1.4):

.

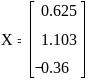2.1.4. Задание. Для всех вариантов с 1 – 15 студенты самостоятельно выписывают системы линейных уравнений, состоящих из двух и более уравнений, определитель которых не равен нулю, а затем их решают методом обратной матрицы.

2.1.5. Вопросы для самопроверки

1. Какая система уравнений является линейно-независимой?

2. Что такое обратная матрица?

Лабораторная работа № 2.2 (С:\USERS\GROUP\NOF\lab2.mcd)

Решение нелинейного уравнения графическим методом

2.2.1. Цель работы. Получение практических навыков алгоритмизации и программирования алгоритма решения нелинейного уравнения графическим методом.

2.2.2. Справочный материал. Графический метод решения нелинейных уравнений является визуальным методом выявления всех корней уравнений в исследуемой области. Алгоритм решения нелинейного уравнения F(x) = 0, xa,b сводится к следующему. Линейные члены уравнения переносятся в правую часть и строятся графики левой и правой частей уравнения на отрезке a,b. Точки пересечений графиков и определяют значения корней.

2.2.3. Пример. Вычислить графическим методом значение корня следующего уравнения:

sin(x) – x + 1 = 0 , x0 3. (2.2.1)

Запишем уравнение (2.2.1) в виде:

sin(x) = x – 1 , ( 2.2.2)

а затем построим графики левой и правой частей уравнения (2.3.2) по следующему алгоритму:

F(x) := sin(x) f(x) := x – 1

a := 0 b := 3 N := 50

h := ( b – a ) / N i := 0 ; N

x_i := a + i * h

Алгоритм построения графиков заключается в следующем. На первом этапе построенния вызывается шаблон графика и подписываются координатные оси, как это указано на рис. 2.2.1, на втором – дважды щелкнув левой клавишей «мышки» в поле графика вызывается процедура обработки графика. Выбираем первую позицию «Кординаты Х и У» координатную сетку, указывая число линий по осям Х и У таким образом, чтобы одна из вертикальных линий пересекала точку пересечения графиков, тем самым определяя значения корня, а горизонтальная – значение F(0).

Рис. 2.2.1. Вычисление корня нелинейного уравнения (2.2.1) как

точки пересечения графиков х = 1,93

Рассмотрим решение кубического алгебраического уравнения, имеющего три действительных корня:

- х³ + bх + c = 0; x-5, 5. (2.2.3)

Уравнение (2.3.3) приведем к виду:

х³ = bх + c , (2.2.4)

и построим графики левой и правой частей уравнения (2.2.4) по алгоритму приведенному выше, подбирая коэффициенты b и c таким образом, чтобы уравнение (2.2.3) имело три действительных корня:

Рис. 2.2.2. Вычисление корней нелинейного уравнения (2.3.3), как

точек пересечения графиков х₁ = - 2,8; х₂ = 0; х₃ = 3,2

2.2.4. Задание. Найти значения корней уравнения, подбирая значения коэффициентов b и c:

.

2.2.5. Вопросы для самопроверки

1. Каким образом нужно переписать уравнение, чтобы решить его графическим методом?

2. Как найти цену делений по осям?

Лабораторная работа № 2.3 (С:\USERS\GROUP\NOF\lab3.mcd)