Министерство образования РФ

Санкт-Петербургский государственный электротехнический

университет «ЛЭТИ»

Кафедра САПР

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 4

по учебной дисциплине «методы оптимизации»

на тему «Исследование градиентных методов»

Вариант 1

Выполнили:

Смирнов С.А.

Маркосов А.С.

Баранов А.А.

Группа: 5372

Факультет: КТИ

Проверил:

(должность, Ф.И.О.)

Санкт-Петербург

2007

Оглавление:

Задание…………………………………………………………………………….3

Описание методов оптимизации…………………………………………………3

Спецификация программы……………………………………………………….4

Листинг программы ……………………………………………………………...5

Результаты тестирования и Выводы…………………….……………………….7

Ответы на контрольные вопросы………………………………………………...8

Задание:

Цель работы – разработка программы многомерной минимизации целевых функций на основе применения простых градиентных методов поиска.

Методы многомерной оптимизации:

М1 – метод Коши;

Функция y(x)	Начальная точка (x1)t	Значение минимума (x*)t
100(x2 – x12)2 + (1 – x1)2	(–1.2; 1) (1.5; 2) (–2; –2)	(1; 1)

Описание методов оптимизации:

Метод Свенна 4.

Начальный этап. Для запуска метода необходимо:

(1) задать x₀ – начальная точка.

(2) выбрать шаг h равным 0.001 или min{η,|(y₁-y’)/y’₁|}, где η=1,2.

(3) выбрать направление поиска p.

Основной этап

Шаг 1. Установить направление убывания функции. h=h, если y’(x₀,p)<0 и h=-h, если y’(x₀,p)>0.

Шаг 2.Двигаться в направлении р, вычисляя значение функции в точках x_k+1=x_k+h_k*p, h_k=2h_k-1. Пока производная не поменяет знак, т.е. Y’_m-1*Y’_m<0

Шаг 3. Фиксируем начальный интервал: [X_m-1,X_m]

Метод Дэвидона.

Этот метод является аналогом метода кубической аппроксимации в задачах поиска минимума функции нескольких переменных по заданному направлению. Идея метода заключается в том, чтобы на ТИЛ найти аппроксимирующий минимум строя полином 3-го порядка.

Начальный этап:

1. Взять ε, х ₀ – начальную точку поиска, p – направление поиска.

2. Найти начальный шаг α₁ = min{ η,|(y₁-y’)/y’₁|}, где η=1,2. y₁=y(x₁), y’₁ =y’(x₁,p)

3. Получить начальный интервал поиска [a,b] методом Свенна 4.

Основной этап:

1. Найти аппроксимирующий минимум, т.е. точку r по формулам:

r = a+α_r *p

α_r = α _a +γ*( α _b - α_a )

γ=(z-f’_a+W)/(f’_b-f’_a+2*W)

W=√z²-f’_a*f’_b

z=f’_a+f’_b+3*(f_a-f_b)/(b-a)

2. Проверить КОП если Y’r<=ε, то остановиться. X= a+ α_r *p Иначе сократить ТИЛ двумя способами:

Y’r<0 -> [r,b]

Y’r>0 -> [a,r]

Установить k=k+1 и вернуться на шаг 1.

Можно модифицировать алгоритм – ввести смещение точек на α₀ .

Метод Коши

Начальный этап:

Взять ε - погрешность,

х ₀ – начальную точку поиска,

k=1 – счетчик количества итераций.

Основной этап:

Шаг1: Вычислить антиградиентное направление p_k = - grad (y_k );

Шаг2: Найти оптимальный шаг α_k с помощью метода Дэвидона;

Шаг3: Перейти в новую точку:

- x_k+1= x_k + α_k*p_k ;

- k=k+1;

Шаг4: Проверить КОП (любой): ‌

(1) ||∆ x_k|‌|<= e₁

(2) | ∆y_k‌|<= e₂

(3) ||grad (y_k)‌||<= e₃

(4) ||∆ x_k|‌|/(1+||∆ x_k|‌|)<= e₄

(5) ||grad (y_k)‌||/(1+||grad (y_k)‌||)<= e₅

Если КОП выполняется остановимся x_* = x_к+1 , иначе вернуться на

Шаг1.

Блок-схемы использованных методов.

Метод Свенна

h1=0.1*|x1|

x2=x1+h1

x1=x2; x2=x1+h;

h=2*h;

Меняем местами а и b

h=-h;

x2=x1+h;

Да

Нет

Нет

Да

Нет

Да

Метод Дэвидона

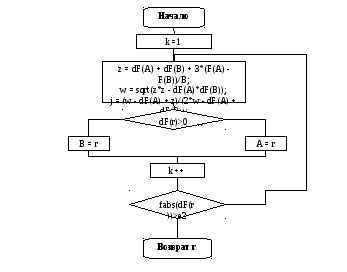
Спецификация программы:

Текст программы:

Результаты тестирования метода:

Ниже приведена таблица с результатами работы программы для функции f(x) = 100(x₂ - x₁²)² + (1 - x₁)², с различными стартовыми точками и точностями вычисления.

Точность:		0.0001		0.00001		0.000001
Метод Коши	К	x*	K	x*	K	x*
X0=(1.2,1)	6241	(0.999902, 0.999803)	9625	(0.999991, 0.999981)	14207	(0.999999, 0.999998)
X0=(1.5,2)	614	(1.00011, 1.000221)	812	(1.000011, 1.000022)	1106	(1.000001, 1.000002)
X0=(-2,-2)	5704	(0.999899, 0.999797)	7410	(0.99999, 0.99998)	9114	(0.999999, 0.999998)

Выводы:

В данной работе был использован метод Свенна4 и метод Дэвидона для получения оптимального шага. Поиск ведется в пространстве, начиная с заданной начальной точки x₀ по антиградиентному направлению p₀. И в результате выполнения метода Коши находится оптимальный шаг, доставляющий минимум в результате исчерпывающего спуска вдоль антиградиентного направления p_к. Полученный шаг соответствует точке x_* = x_к+1 . Большое количество итераций и неточность минимума объясняется тем, что вблизи минимума для реальных (овражных) функций метод зацикливается, либо рыскает и останавливается.

Ответы на контрольные вопросы:

1. Поясните организацию линейного поиска на основе методов золотого сечения, Фибоначчи и Пауэлла.

Организация поиска минимума функции многих переменных в заданном направлении аналогична поиску минимума целевых функции. Различие заключается в описании (задании) функции, а также в методе Свенна, при помощи которого производится нахождение интервала локализации минимума.

Рассмотрим метод Свенна для функции многих переменных.

Его отличие заключается в том, что для опредения направления убывания функции мы определяем значение производной функции в нуле. Если оно больше нуля тогда знак шага фукции a меняется на противопложный. А удвоение шага происходит до тех пор пока не поменяет знак значения произведения производных функции на концах отрезка.

В своей работе я задавал функцию описывая каждую переменную через шаг функции - a.

Методы золотого сечения и метод Пауэлла приведены в данном отчёте в пункте описания методов оптимизации.

2. Найти производную dfx в точке x¹=(1,0)^t по направлению p¹=(1,1)^t для функции

f(x) = x1² – x1x2 + 2*(x2)² - 2x1.

g1=2x1-x1-2=2-2=0.

g2=-x1+4*(x2)= -1

Таким образом dfx = g1*p1 + g2*p2 = 0*1 + (-1)*1 = -1.

3. Как изменится процедура минимизации методами Больцано, дихотомии, ДСК, Дэвидона при переходе от поиска на числовой прямой к поиску на плоскости R²?

При минимизации вышеуказанными методами на числовой прямой направление всегда фиксировано и задается во всех используемых методах изначально. При поиске на плоскости применяются градиентные методы, в которых направленеи изменяется, т.е. необходимо подавать не постонные значения направления, а переменные.

4. Что является направлением наискорейшего спуска в точке x = (1,1)^t для целевой функции y(x) = x₁² + 2x₂² ?

Направлени наискорейшего спуска.

(вычислим антиградиентное направление движения)

5. Найдите минимум y(x) = x₁² - x₁x₂ + 2x₂² - 2x₁ + e^x1+x2, двигаясь из точки x = (0,0) в направлении наискорейшего спуска.

- (0.4998;-0.4998)

9