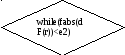Министерство образования рф

Санкт-Петербургский государственный электротехнический
университет «ЛЭТИ»

Кафедра САПР
Отчет по лабораторной работе № 3
по учебной дисциплине «методы оптимизации»
на тему «Исследование методов полиномиальной интерполяции для поиска минимума целевых функций»
Вариант 1
Выполнили:
Смирнов С.А.
Маркосов А.С.
Баранов А.А.
Группа: 5372
Факультет: КТИ
Проверил:
(должность, Ф.И.О.)
Санкт-Петербург
2007
Оглавление:
Задание…………………………………………………………………………….3
Описание методов оптимизации…………………………………………………3
Спецификация программы……………………………………………………….4
Листинг программы ……………………………………………………………...5
Результаты тестирования и Выводы…………………….……………………….7
Ответы на контрольные вопросы………………………………………………...8
Задание:
Цель работы – разработка программы, реализующей комбинированную процедуру минимизации функции многих переменных в заданном направлении.
Методы линейного поиска:
М1 – метод золотого сечения-2 – Дэвидона;
|
Функция y(x) |
Начальная точка (x1)t |
Направление поиска pt |
Значение минимума (x*)t |
|
x12 + 3x22 + 2x1x2 |
(1; 1) |
(2; 3) |
(0.2558; –0.1163) |
Описание методов оптимизации:
Метод Свенна:
С помощью этого метода получаем начальный интервал локализации минимума.
Начальный этап:
1) задать x0 – произвольная начальная точка.
2) выбрать шаг h равным 0.001 или 0.01*|x0|.
Основной этап:
Шаг 1:
Установить направление убывания целевой функции. Для этого надо взять x2=x1+h. Если f1<f2, то надо поменять направление движения(h=-h и взять x2=x1+h).
Шаг 2:
Вычислять fk в точках xk+1=xk+hk, где hk=2hk-1, k=2,3,…,n-1 до тех пор пока не придём в точку xn такую что fn>fn-1.
Шаг 3:
Установить начальный интервал локализации минимума a1=xn-2 и b1=xn.
Метод Свенна 4.
Начальный этап. Для запуска метода необходимо:
(1) задать x0 – начальная точка.
(2) выбрать шаг h равным 0.001 или min{η,|(y1-y’)/y’1|}, где η=1,2.
(3) выбрать направление поиска p.
Основной этап
Шаг 1. Установить направление убывания функции. h=h, если y’(x0,p)<0 и h=-h, если y’(x0,p)>0.
Шаг 2.Двигаться в направлении р, вычисляя значение функции в точках xk+1=xk+hk*p, hk=2hk-1. Пока производная не поменяет знак, т.е. Y’m-1*Y’m<0
Шаг 3. Фиксируем начальный интервал: [Xm-1,Xm]
Метод Золотого Сечения 2. (для функции нескольких переменных)
Метод Золотого Сечения является процедурой линейного поиска минимума унимодальной функции f(x) на интервале [a, b], отличающейся тем, что на каждой итерации очередная пробная точка делит интервал локализации в отношении постоянном для всех интервалов τ=L2/L1=L3/L2=...Ln/Ln-1.
Начальный этап
(1) Задать константу , начальный интервал [a1, b1] вычисляется методом Свенна.
(2) Вычислить одну стартовую точку x1 = a1 + 0.618L*p L=|a-b|
(3) Положить k = 1.
Основной этап
Шаг 1. Взять очередную точку x2=a1+b1-x1 симметричную исходной x1 и сократить ТИЛ рассмотрением четырёх ситуаций: если x1<x2 и f(x1)<f(x2) то ak+1=ak, bk+1=x2, x1=x1; если x1<x2 и f(x1)>f(x2) то ak+1= x1, bk+1= bk, x1=x2; если x1>x2 и f(x1)<f(x2) то ak+1=x1, bk+1= bk, x1=x1; если x1>x2 и f(x1)>f(x2) то ak+1=ak, bk+1=x1, x1=x2.
Положить k=k+1.
Шаг 2. Проверить критерий окончания поиска: если |a-b| < фиксируем аппроксимирующий минимум x*=(a+b)/2.
и на Шаг 1.
Метод Дэвидона.
Этот метод является аналогом метода кубической аппроксимации в задачах поиска минимума функции нескольких переменных по заданному направлению. Идея метода заключается в том, чтобы на ТИЛ найти аппроксимирующий минимум строя полином 3-го порядка.
Начальный этап:
-
Взять ε, х 0 – начальную точку поиска, p – направление поиска.
-
Найти начальный шаг α1 = min{ η,|(y1-y’)/y’1|}, где η=1,2. y1=y(x1), y’1 =y’(x1,p)
-
Получить начальный интервал поиска [a,b] методом Свенна 4.
Основной этап:
-
Найти аппроксимирующий минимум, т.е. точку r по формулам:
r = a+αr *p
αr = α a +γ*( α b - αa )
γ=(z-f’a+W)/(f’b-f’a+2*W)
W=√z2-f’a*f’b
z=f’a+f’b+3*(fa-fb)/(b-a)
-
Проверить КОП если Y’r<=ε, то остановиться.X= a+ αr *p Иначе сократить ТИЛ двумя способами:
Y’r<0 -> [r,b]
Y’r>0 -> [a,r]
Установить k=k+1 и вернуться на шаг 1.
Можно модифицировать алгоритм – ввести смещение точек на α0 .
Блок-схемы использованных методов.
Метод Свенна
h1=0.1*|x1|
x2=x1+h1
x1=x2;
x2=x1+h;
h=2*h;
Меняем местами а
и b
h=-h;
x2=x1+h;
Да
Нет
Нет
Да
Нет
Да
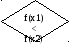


















Метод Золотого сечения 2:
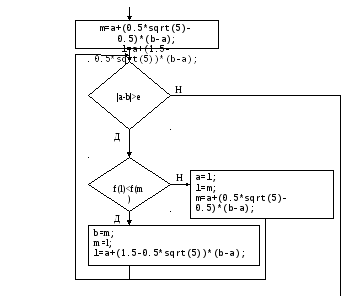



x=(a+b)/2;
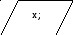
Метод Дэвидона:


z=dF(A)+ dF(B) +
3*(f(A)-f(B))/B

w=sqrt(z*z - dF(A)*dF(B))

j=(w - dF(A) + z)/(2*w -
dF(A) + dF(B))
r=A + (B-A)*j


B = r

 Нет
Нет
A = r