Детектирование сигналов с линейными видами модуляции

На вход детектора, тип которого и виды модуляции при различных вариантах указан в табл. П3, подается модулированный сигнал.

Требуется:

1.Рассчитать и построить спектральные диаграммы на входе и выходе детектора с соблюдением масштаба по обеим осям.

2.Нарисовать временные диаграммы сигнала на входе и выходе детектора.

3.Пояснить, в каких случаях детектирование не сопровождается искажениями и почему.

4.Для вариантов 25-99, в которых используется синхронный детектор, пояснить, к чему приведет неточное восстановление частоты несущего колебания на приемной стороне. Для определенности принять неточность восстановления несущего колебания ∆w=0.1*Ω. Построить с учетом этого спектральную диаграмму на выходе ФНЧ детектора.

Решение:

1. Спектральные диаграммы на входе и выходе детектора.

_{На вход детектора подается однополосный модулированный сигнал:}

[М]

Определим коэффициент глубины модуляции m, по формуле:

, где n-последняя цифра номера зачетной книжки.

m=0.5

_{- круговые частоты, измеряемые в рад/с. Для всех вариантов частота несущего колебания , где - частота модулирующего сигнала, амплитуда .}

Таким образом, спектральная диаграмма на входе детектора:

Идеальный синхронный детектор перемножает входное колебание ОМ на восстановленную несущую. Если несущая восстановлена точно по частоте и фазе, то в результате перемножения появится неискаженный продукт детектирования.

Угловая (чм и фм) модуляция

В системе передачи непрерывных сообщений в качестве модулятора используется для нечетных вариантов частотный модулятор, для четных вариантов – фазовый модулятор.

Модулирующим сигналом во всех случаях является низкочастотный гармонический сигнал .

Средняя частота несущего колебания .

Амплитуда несущего колебания для всех вариантов, коэффициент пропорциональности k соответствует крутизне модуляционной характеристики модулятора.

Требуется:

1.Записать аналитическое выражение ФМ сигнала.

2.Рассчитать индекс модуляции ФМ сигнала и девиацию частоты .

3.Рассчитать максимальную частоту и минимальную частоту ФМ сигнала и приблизительно построить временную диаграмму ФМ сигнала на одном периоде модулирующего сигнала .

4.Найти спектр и построить спектрограмму ФМ сигнала в полосе частот от до .

5.Найти спектр и построить спектрограмму ФМ сигнала для случая, когда один из параметров модулирующего сигнала (A или F) изменится (увеличиться или уменьшится) в 2 раза (см. табл. П4). Пусть при этом не изменяется.

Решение:

1. Аналитическое выражение ФМ сигнала.

_{Для составления аналитического выражения ФМ сигнала необходимо в квазигармоническое представление сигнала} вместо подставить прямо пропорциональное модулирующему сигналу изменение фазы:

[М]

_{, пусть φ=0.}

_{Таким образом получается,}

2. _{Индекс модуляции ФМ сигнала и девиация частоты.}

_{Индекс модуляции M – максимальное отклонение фазы от среднего значения.}

_{Соответсвенно:}

Девиация частоты - максимальное отклонение частоты от ее среднего значения.

Для определения девиации частоты воспользуемся связью частоты и фазы сигнала:

[М]

Максимальное отклонение от среднего значения частоты будет при

Так как f0=12F, то:

3. Рассчитать максимальную и минимальную частоту ФМ сигнала и приблизительно построить временную диаграмму ФМ сигнала на одном периоде модулирующего сигнала.

Максимальная частота:

Минимальная частота:

Временную диаграмму ФМ сигнала удобно строить, ориентируясь на изменение частоты. В нашем случае частота ФМ сигнала изменяется по закону синуса:

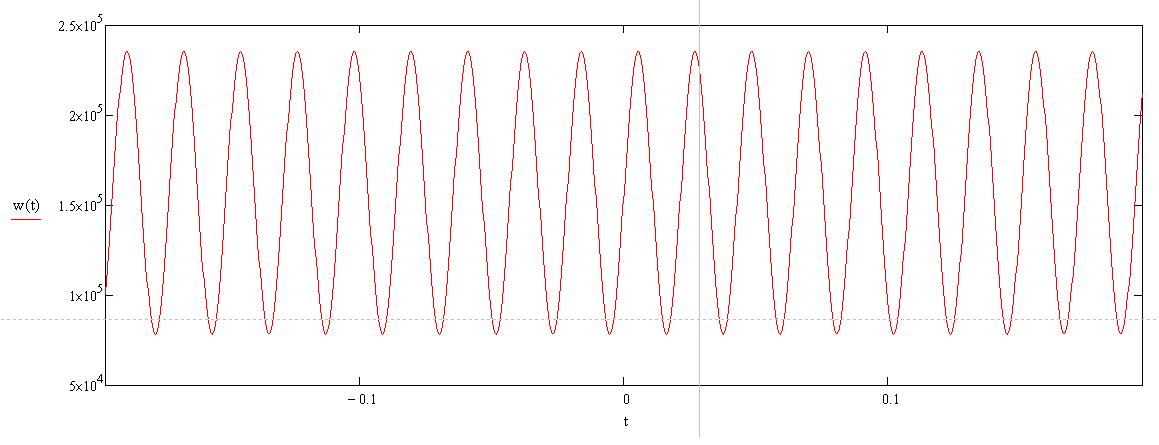
4. Найти спектр и построить спектрограмму ФМ сигнала в данной полосе частот.

Полоса частот в которой необходимо построить спектрограмму ФМ сигнала:

от

до

Для расчета спектров ФМ колебаний в случае модуляции гармоническим сигналом необходимо воспользоваться графиками бесселевых функций первого рода n порядка от аргумента M (M=4).

Для вычисления бесселевых функций воспользуемся формулой:

[М]

, где n – порядок бесселевых функций.

При этом отметим, что функции Бесселя первого рода с порядком n от аргумента M обладают следующим свойством:

В

В

В

В

В

В

В