2.1.4. Метод Полака-Ривьера
Описание метода
Итерационная
формула метода
,
где
,
;
Т.о. на каждом шаге используется дополнительная процедура одномерной минимизации.
Этот метод удобнее применять для произвольных (неквадратичных) функций.
Рекомендуется применять процедуру обновления, т.е. через каждые n-шагов происходит сдвиг в направлении антиградиента.
То есть 0 = 0, затем n=0...... mn=0, следовательно, pk= -f(xk)+0*pk-1= -f(xk)
(сдвиг в направлении антиградиента)
По скорости сходимости n шагов метода сопряженного градиента эквивалентны одному шагу метода Ньютона (для квадратичной функции метод сходится за один шаг).
Испытание метода
b=0
|
x0 |
(3 , 8) |
(3, 10) |
(10, 20) | |||
|
a |
0.1 |
1 |
0.1 |
1 |
0.1 |
1 |
|
k* |
19 |
5 |
2 |
5 |
11 |
5 |
|
f(xk*) |
8.100 |
81.000 |
8.100 |
81.000 |
8.100 |
81.000 |
b=3
|
x0 |
(3 , 8) |
(3, 10) |
(10, 20) | |||
|
a |
0.1 |
1 |
0.1 |
1 |
0.1 |
1 |
|
k* |
~17(*) |
16 |
~6(*) |
8 |
~8(*) |
27 |
|
f(xk*) |
- |
0.16884330 |
- |
0.1681812 |
- |
0.16891264 |
(*)-начиная с данного шага значение координат (x,y) колеблются относительно точки минимума в пределах (~2,6 ; ~2,9) и (~0,6 ; ~0,7) соответственно
Итерационный процесс для x0 = (3, 10), a = 0.1, b=3:
|
шаг x1 x2 f 1 2.732433 0.668926 0.02514763 2 2.524426 0.588389 0.06313869 3 2.308301 0.510261 0.23569079 4 2.330130 0.700857 0.22548267 5 2.758470 0.679383 0.02470704 6 2.744701 0.673843 0.02486549 7 2.945863 0.757156 0.03287421 8 2.670740 0.644485 0.02900558 9 2.788501 0.691549 0.02487229 10 2.669593 0.644034 0.02912217 11 2.819262 0.704128 0.02564847 12 2.653191 0.637618 0.03099532 13 2.800676 0.696513 0.02511369 14 2.658497 0.639690 0.03034596 15 2.810033 0.700341 0.02535919 16 2.654844 0.638263 0.03078848 17 2.804997 0.698280 0.02522085 18 2.656430 0.638883 0.03059389 19 2.807599 0.699345 0.02529056 20 2.655483 0.638513 0.03070962 |
2.2. Mетод условного градиента
Описание метода
В очередной точке
xk
линеаризуют функцию f(x)
(в этом «условность» метода, то есть
линеаризация и есть «условие» в названии).
Затем решают задачу min
линейной функции на X
и найденную точку
используют
для выбора направления движения.
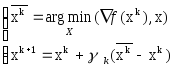
При этом предполагается:
Задача минимизации линейной функции на X имеет решение.
Это решение может быть найдено достаточно просто, лучше всего в явной форме.
Нужно указать правило выбора k. Можно k определить из условия наискорейшего спуска:
В этом случае последовательность xk сходится к специальной точке. В частности для гладких функций f верно: f(x*)- f* = o(1/k), где f* = min f(x) на множестве X.
Исследование метода
b=0
|
x0 |
(3 , 8) |
(3, 10) |
(10, 20) | |||
|
a |
0.1 |
1 |
0.1 |
1 |
0.1 |
1 |
|
x20 |
(0.000; 0.000) |
(0.000; 0.000) |
(0.000; 0.000) |
(0.0; 0.000) |
(0.000; 0.000) |
(0.000; 0.000) |
|
f(x20) |
8.100 |
81.000 |
8.100 |
81.000 |
8.100 |
81.000 |
|
k* |
3 |
1 |
2 |
1 |
3 |
1 |
|
f(xk*) |
8.100 |
81.000 |
8.100 |
81.000 |
8.100 |
81.000 |
b=3
|
x0 |
(3 , 8) |
(3, 10) |
(10, 20) | |||
|
a |
0.1 |
1 |
0.1 |
1 |
0.1 |
1 |
|
x20 |
(2.764987; 0.691008) |
(2.532732; 0.591504 ) |
(2.791195; 0.698552) |
(2.566343; 0.605923) |
(2.787283; 0.694898) |
(2.534755; 0.604502 ) |
|
f(x20) |
0.02585042 |
0.17008567 |
0.02571280 |
0.17015941 |
0.02536510 |
0.18038547 |
|
k* |
60 |
88 |
71 |
77 |
80 |
69 |
|
f(xk*) |
0.02468595 |
0.16861399 |
0.02468595 |
0.16861399 |
0.02468595 |
0.16861399 |
Итерационный процесс для x0 = (3, 8), a = 0.1, b=0:
|
№ x1 x2 f(x1,x2) 1 -0.997973 0.150731 10.84665999 2 -0.659732 0.180908 10.42718625 3 0.000000 0.000000 8.10000000 |
Метод функции Лагранжа
Описание метода
Функцией Лагранжа называется функция:
(x ,)
= f(x)+
f(x) + (
,g(x)),где
i
0.
Если выполняется соотношение
(x* , ) (x* ,*) (x ,*) xRn, 0,
то точка x* является оптимальной точкой задачи выпуклого программирования.
Это соотношение можно записать иначе:
(*)
(x*
,*)
=
(x
,)
=
(x
,)
= f(x*)
Свойства модифицированной функции Лагранжа.
Если + k g(x)>0, то
-
добавка (штраф) за то, что g(x)>0.
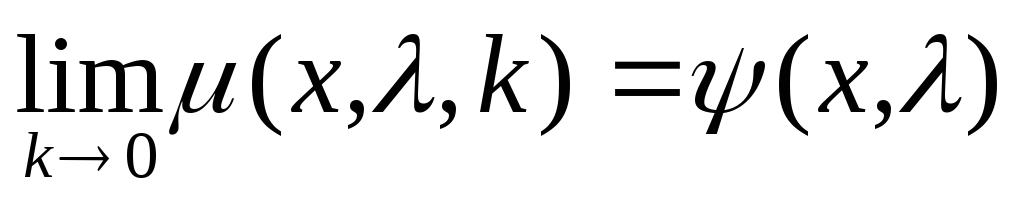(функция
Лагранжа),
иначе
Метод модифицированной функции Лагранжа.
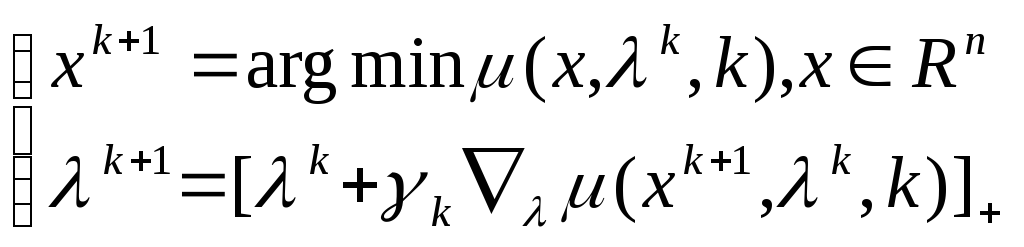
Метод сходится к (x* ,*) со скоростью геометрической прогрессии.
Испытания метода:
b=0
|
x0 |
(3 , 8) |
(3, 10) |
(10, 20) | |||
|
a |
0.1 |
1 |
0.1 |
1 |
0.1 |
1 |
|
k* |
1 |
11 |
1 |
11 |
7 |
5 |
|
f(xk*) |
8.77081 |
81.000 |
8.98315 |
81.000 |
8.10589 |
81.000 |
|
Множители L1(xk*) Лагранжа L2(xk*) |
0.59156 |
2.69962 |
0.58339 |
2.69966 |
0.00000 |
2.69731 |
|
0.00000 |
2.69963 |
0.00000 |
2.69966 |
0.54123 |
2.69738 | |
b=3
|
x0 |
(3 , 8) |
(3, 10) |
(10, 20) | |||
|
a |
0.1 |
1 |
0.1 |
1 |
0.1 |
1 |
|
k* |
1 |
1 |
1 |
1 |
6 |
1 |
|
f(xk*) |
0.03072 |
0.16861 |
0.03113 |
0.16861 |
0.02556 |
0.16861 |
|
Множители L1(xk*) Лагранжа L2(xk*) |
0.00000 |
0.00000 |
0.00000 |
0.00000 |
0.00000 |
0.00000 |
|
0.00929 |
0.04525 |
0.00958 |
0.04525 |
0.00715 |
0.04527 | |
Итерационный процесс для x0 = (3, 8), a = 1, b=0:
|
шаг x1 x2 l1 l2 f 1 0.00001 -0.11765 0.00000 0.00000 74.62383 2 0.00001 -0.11765 2.36679 2.36682 85.82732 3 0.00001 -0.01451 4.73357 4.73363 82.27842 4 0.00000 0.08845 5.02407 5.02415 76.38848 5 -0.00000 0.10108 3.26286 3.26294 83.40075 6 -0.00001 0.02450 1.25145 1.25152 82.69320 7 -0.00001 -0.06309 0.76205 0.76210 77.92963 8 -0.00001 -0.08442 2.02788 2.02789 82.01202 9 -0.00001 -0.02927 3.72351 3.72349 82.59435 10 -0.00001 0.04453 4.30978 4.30973 79.04749 11 0.00000 0.07004 3.42110 3.42103 81.23084 12 0.00000 0.03138 2.02530 2.02523 82.29725 13 0.00000 -0.02938 1.39862 1.39857 79.86569 14 0.00000 -0.05668 1.98701 1.98697 80.85995 15 0.00000 -0.03105 3.12388 3.12386 81.97095 |
Итерационный процесс для x0 = (3, 10), a = 1, b=3:
|
шаг x1 x2 l1 l2 f 1 2.56484 0.60116 0.00000 0.00000 0.16753 2 2.56484 0.60116 0.00000 0.04623 0.16967 3 2.56348 0.60308 0.00000 0.09246 0.16863 4 2.56211 0.60500 0.00000 0.09292 0.16756 5 2.56211 0.60502 0.00000 0.04760 0.16963 6 2.56344 0.60314 0.00000 0.00183 0.16865 7 2.56479 0.60124 0.00000 0.00093 0.16758 8 2.56480 0.60120 0.00000 0.04535 0.16959 9 2.56350 0.60305 0.00000 0.09066 0.16867 10 2.56217 0.60493 0.00000 0.09198 0.16760 11 2.56215 0.60499 0.00000 0.04845 0.16955 12 2.56341 0.60317 0.00000 0.00360 0.16869 13 2.56473 0.60131 0.00000 0.00186 0.16762 14 2.56476 0.60123 0.00000 0.04452 0.16951 15 2.56353 0.60301 0.00000 0.08891 0.16871 |