Министерство образования РФ

Санкт-Петербургский государственный

Электротехнический университет «ЛЭТИ»

Отчет

по лабораторной работе N6

«.Исследование модификаций ньютоновских оптимизационных процессов»

Вариант 1

Выполнили: студенты гр. 3371

Мифтахетдинов Э.

Кохтенко Н.

Проверил: преподаватель

Выборнов Д.М.

Санкт-Петербург

2005 Содержание:

1) Цель работы ---------------------------------------3

2) Краткое описание метода оптимизации----------------3

3) Пооператорная блок-схема---------------------------4

4) Спецификация программы-----------------------------6

5) Текст программы------------------------------------7

6) Результаты тестирования программы-----------------13

7) Ответы на контрольные вопросы---------------------13

8) Выводы по работе----------------------------------14

1) Цель работы и требования задания

1.1) Цель работы

Изучение метода Ньютона и его модификаций, а также разработка программы, удовлетворяющей требованиям лабораторной работы 5.

.

Дано: функция f(x) = 100(x₂–x₁²)²+ (1 –x₁)²

Функция f2(x) = (x₁– 1)²+ (x₂– 3)²+ 4(x₃+ 5)²

начальная точка x₁ = (1.5;2);

Для f2(x) - (4; –1; 2);

точность локализации минимума  = 10^–3;

Значение минимума x^* = (1; 1)

Для f2(x) – x^* = (1; 3; –5)

Найти: минимум (x_min = ?).

2) Краткое описание метода оптимизации

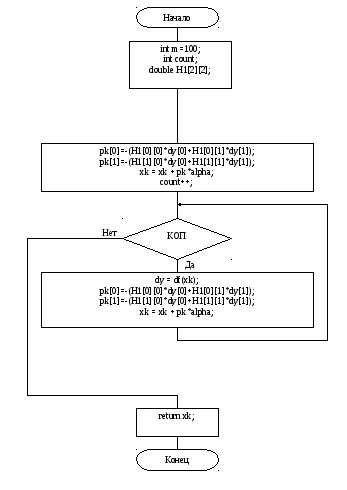
2.1) Обобщенный метод Ньютона

Модификации метода ньютона направлены на:

-снижение чувствительности к выбору начальной точки;

-уменьшение затрат на вычисление обратной матрицы;

-сохранение положительной определенности гессиана во всех точках вычисления;

-уменьшение объема вычислений при расчете вторых производных, т.е. минимизировать затраты на решение СЛАУ;

-обеспечение релаксационного процесса при котором .

Отличительной особенностью обобщенного метода Ньютона является выбор шага Alpha и минимизация целевой функции по Alpha вдоль полученного направления P.

Реализуется следующим алгоритмом:

Начальный этап:

Задать произвольную начальную точку x₀Rⁿ ;

Задать точность вычислений Eps1=Eps2=0.0000001-0.0001;

Задать кол-во шагов M=100 (например);

Положить счетчик итераций К=1;

Основной этап:

Шаг 1. Установить направление поиска минимума. Для этого взять p^k=-(H^k)^-1g^k.

Шаг 2. Минимизировать целевую функцию по Alpha вдоль полученного p^k.

Шаг 3. Перейти в новую точку X^k+1=X^k+alpha^kp^k.

Шаг 4. Проверить КОП (например, К≥М или (норма градиента)≤eps)

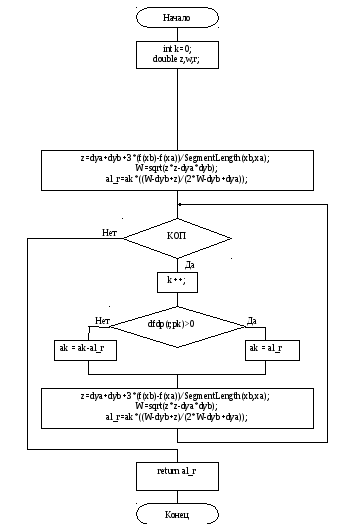
2.2) Метод Давидона:

Начальный этап:

Задать Eps, p, x^k;

Выбрать начальный шаг по формуле Давидона, предварительно вычислив производную по направлению;

Реализовать Svenn-4 для установления интервала [Alpha_a, Alpha_b];

Основной этап:

Шаг 1. Найти аппроксимирующий шаг Alpha_r = Alpha_b(W-Y’_a+Z)/(2*W-Y’_a+Y’_b)

r = a+Alpha*p

Шаг 2. Проверить КОП (Y’_r ≤ Eps). Если КОП выполняется, то СТОП, найден шаг, а значит и минимум, иначе сократить ТИЛ рассмотрением двух ситуаций:

1. Если Y’_r ≥ 0, тогда Alpha_b=Alpha_r

2. Если Y’_r < 0, тогда Alpha_b= Alpha_b -Alpha_r

3. Пооператорная блок-схема

3.1) Метод Давидона:

3.2) Обобщенный метод Ньютона:

4) Спецификация программы

Point – реализованный класс.

Имя функции	Назначение	Входные параметры	Возвращаемое значение
main	Главная функция в программе, в которой и реализуется метод Свенна и метод Золотого сечения - 1
fabs	Реализует значение по модулю	Point &p	result
f	Задание функции	Point &p	100(x2–x12)2+ (1 –x1)2
dfitd	Реализация производной по направлению	Point &x, Point &p	(f(x1)-f(x2))/(2*alpha)
df	Реализация разностной производной	Point &x
min	Реализация выбора минимального из двух	X,Y	Либо X, либо Y
SegmentLength	Вычисление длины отрезка	Point &x, Point &y	Либо sqrt(ans), либо -sqrt(ans)
Svenn4	Нахождение начального интервала локализации для метода Давидона	dy1, Point &pk1, Point &xk1, ak, Point &xa, Point &xb
KOP	Реализует функцию критерия окончания поиска	Point &x, epsilon	stop
ON	Реализация обобщенного метода Ньютона	*xk1, eps	xk
FindAlpha	Метод Давидона	Point &pk1, Point &xk1, eps	al_r