Требования задания.

Целью работы является:

1. Сравнение двух методов одномерной минимизации – прямого и

интерполяционного.

2. Разработка программы, реализующей прямой метод на этапе установления границ начального интервала и метод полиномиальной интерполяции для

локализации искомого минимума.

4х³ - 3х⁴, если х≥0

f(x) = 

4х³ + 3х⁴, если х<0

х0=0,4

e=0.001

Контрольный ответ х*=-1,0000000;

метод Больцано - Пауэлла;

Таким образом:

1. по заданной начальной точке методом Свенна-1 локализуем точку минимума.

2. Выполняем несколько итераций метода Больцано, постепенно сокращая начальный интервал локализации, наёденный методом Свенна.

3. Интервал, найденный за несколько итераций метода Больцано передаём в качестве начального в метод Пауэлла, таким образом разгоняя этот метод.

4. по достижении КОП вычисляем минимум функции.

Описание методов оптимизации.

Метод Свенна:

Начальный интервал локализации минимума унимодальной функции f(х) определяется методом Свенна.

Начальный этап:

(1) Дана начальная точка х R . Дается начальный шаг

h =х =(0,10,01)*| x|

Основной этап:

Шаг 1. Установить направления убывания функции. Возьмём

х= х+ h,и если f > f ,направление движение необходимо поменять: h:= - h

и взять х= х+ h

Шаг 2. Вычислить функцию f в точках х, х, … по формуле

x = x+ h где, h= 2*h, k=2, 3, ………, n-1

до тех пор, пока не придем в точку х , такую, что f > f

(пока функция не возрастает)

Шаг 3.Установить начальный интервал локализации минимума. Так мы могли проскочить минимум на предыдущем шаге, устанавливаем с запасом:

а=х в= х

x

x x х

Метод средней точки (метод Больцано)

Данный метод является вариантом метода деления интервала пополам.Последовательные сокращения интервала неопределенности производятся на основе оценки производной минимизируемой функции в центре текущего интервала.

Начальный этап. Для запуска метода необходимо:

(1) задать [a₁,b₁]- начальный интервал локализации минимума, на границах которого знаки производных различны, т.е. f'(a₁)f'(b₁)<0;  - малое положительное число;

(2) положить к=1 и перейти к основному этапу.

Основной этап

Шаг 1. Взять пробную точку х_k в центре текущего интервала и проверить критерий окончания поиска: (1) x_k = (a_k + b_k)/2; (2) если f'(x_k) ≤  и L_k= b_k - a_k≤ , то остановиться (х_k = х* -аппроксимирующий минимум).

Шаг 2. Сократить текущий интервал:

(1) Если f (x_k) > 0, то положить a_k+1 = a_k и b_k+1 =x_k, в противном случае - a_k+1 =x_k, b_k+1 =b_k;

(2) заменить k на k+1 и вернуться на шаг 1.

Метод Пауэлла:

Метод Пауэлла является процедурой интерполяционного поиска минимума унимодальной функции f(x) на замкнутом интервале [a,c].

Этот метод эффективно работает, если h1 достаточно мал и х1 D(x*)

Начальный этап:

Выбрать или получить параметры [a,c] методом Свенна1. b=(a+c)/2.

Выбрать 1=10^(-3)10^(-8) и 2=10^(-3)10^(-8);

Основной этап:

1. Выполнить аппроксимацию по трём точкам a,b и c и найти d по формуле 1

при k=1 или по формуле 2 при k=2, где k – число итераций.

Ф ормула 1:

Формула 2:

2. П роверка близости двух лучших точек:

Если оба критерия выполняются, то стоп – минимум найден , положить x*=(b+d)/2 , иначе

1. x1 = лучшей точке из b или d , т.е. той , в которой значение функции

меньше.

2. Сократить ТИЛ рассмотрением четырёх ситуаций (как в методах

Фибоначчи-2 или ЗС-2).

3. Присвоить точкам новые имена.

4. Вернуться на шаг1 основного этапа.

Блок-схема алгоритма.

Метод Свенна 1:

да

func(х)<func(х )

Нет h=- h

х= х

х=х+h

h=- h

х= х

х=х+h

Да

func(х)<func(х )

Нет

a= х -3*h/2;

b= х;

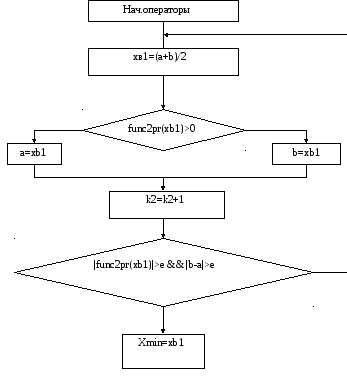
Метод Больцано:

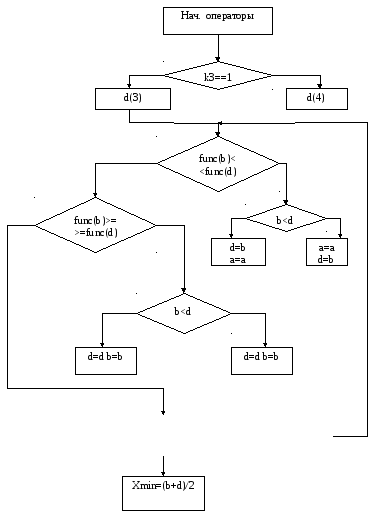
Метод Пуэлла:

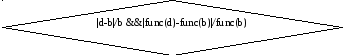
Спецификация:

d(3) - d=b+1/2*( ( (b-pow(a,2))*(func(b)-func(c)) - (b-pow(c,2))*(func(b)-func(a)) )/( (b-a)*(func(b)-func(c))-(b-c)*(func(b)-func(c))));

d(4) - d=b+1/2*( ( (b-a)*(func(a)-func(c)) )/(func(a)-2*func(b)+func(c)));

func - заданная функция.

func2pr- производная функции.

x1 - начальная точка.

h - шаг движения.

x2 - x2=x1+h – cледующая точка.

a - начало интервала в обоих методах .

b - конец интервала в обоих методах.

xb1 - центр интервала .

d - аппроксимирующая точка.

e - погрешность расчёта.

k3 - число итераций метода.

Xmin - точка минимума функции.

Тексты программ.

Т.к. различия в методах начинаются только с этапа поиска минимума – последовательного уменьшения ТИЛ, то сначала целесообразно привести общий фрагмент программы, а именно – метод Свенна1 и определение функций и переменных, а затем отдельно рассмотреть фрагменты различных методов линейного поиска.

#include<iostream.h>

#include<conio.h>

#include<stdio.h>

#include<math.h>

double func(double x)

{if(x>=0)

{return (4*pow(x,3) - 3*pow(x,4));

}

else

{return (4*pow(x,3)+3*pow(x,4));

}

}

double func2pr(double x)

{if(x<=0)

{return (12*pow(x,2)+12*pow(x,3));

}

else

{return (12*pow(x,2)-12*pow(x,3));

}

}

void main(void)

{ double x0=0.4, e=0.001, h, x1, x2, a, b;

h=e*fabs(x0);

x1=x0;

x2=x1+h;

cout<<" S * V * E * N * N"<<endl;

cout<<"h:"<<h<<endl<<"x2:"<<x2<<endl;

cout<<"func x1:"<<func(x1)<<endl;

cout<<"func x2:"<<func(x2)<<endl;

if( func(x1) < func(x2))

{ h = -h;

x2=x1+h;

}

do { h=h*2;

x1=x2;

x2=x1+h;

}

while( func(x2) < func(x1) );

a = x1-h/2;

b = x2;

int musor;

if(a < b)

cout<<"a:"<<a<<endl<<"b:"<<b<<endl;

else

{ musor=b;

b=a;

a=musor;

cout<<"a:"<<a<<endl<<"b:"<<b<<endl;

}

cout<<"B * O * L * C * A * N * O"<<endl;

double xb1;

xb1=(a+b)/2;

cout<<"xb1:"<<xb1<<endl;

double k2;

do{ xb1=(a+b)/2;

if(func2pr(xb1) > 0 )

b=xb1;

else

a=xb1;

k2=k2+1;

}while( fabs(func2pr(xb1))>e && fabs(b-a)>e );

cout<<"Xmin:"<<xb1<<endl;

cout<<"P * A * U * E * L * L * A"<<endl;

double c, d, Xmin2;

a=a;

c=b;

b=(a+c)/2;

int k3=1;

do{

if(k3==1)

{

d=b+1/2*( ( (b-a)*(func(a)-func(c)) )/(func(a)-2*func(b)+func(c)));// formula 4

}

else

{d=b+1/2*( ( (b-pow(a,2))*(func(b)-func(c)) - (b-pow(c,2))*(func(b)-func(a)) )/( (b-a)*(func(b)-func(c))-(b-c)*(func(b)-func(c))));

}

if(func(b)<func(d))

{if(b<d)

{ a=a;

d=b;

}

else

{ d=b;

a=a;

}

}

if(func(b)>=func(d))

{ if(b<d)

{ d=d;

b=b;

}

else

{ d=d;

b=b;

}

}

}

while(fabs((d-b)/b)&& fabs((func(d)-func(b))/func(b)));

Xmin2=(b+d)/2;

cout<<"Xmin2:"<<Xmin2<<endl;

getch();

}

Результаты тестирования программы.

В результате выполнения программы были получены следующие значения:

• В результате работы метода Свенна-1 получен интервал:

[a=-2 , b=0.4188]

• В результате работы метода Больцано получаем точку минимума: х* = -1,000169

• В результате работы метода метода Пауэлла получаем итоговую точку минимума: х* = -0,999783