Содержание
2 5
5
6
7
8
9 9 11 15 17 20
Задание…………………………………………………………………………………….
Определение параметров случайного процесса…………………………………….
1.1. Нахожднние математического ожидания и
дисперсии случайного процесса ………………………………..…………..
1.2. Нахождение корреляционной матрицы
случайного процесса………………………………………………………….
1.3. Проверка стационарности случайного процесса
в широком смысле…………………………………………………………….
1.4. Нахождение нормированной корреляционной
матрицы случайного процесса……………………………………………….
Определение структуры согласованного и квазиоптимального
фильтра………………………………………………………………………………
2.1. Построение согласованного фильтра……………………………………..
2.2. Построение квазиоптимального фильтра……………………………………
Определение характеристик обнаружения………………………………………….
Выводы………………………………………………………………………………….
Литература……………………………………………………………………………..
ЗАДАНИЕ N 1
1.Случайная функция X(t) задана 12 реализациями xi(t) в 21 сечении. Значения реализаций с шагом 0,1 сек заданы в файле в виде матрицы. Вычислить математическое ожидание, дисперсию и корреляционную матрицу случайной функции, проверить, является ли функция X(t) стационарной, и в последнем случае определить ее нормированную корреляционную функцию.
2.На вход приемного устройства поступает сигнал
x(t)=s(t)+n(t), где
s(t) = A exp(-t/t0) cos(w0t+j0) , t ³ 0
A - случайная амплитуда, распределенная по закону Рэлея:
,
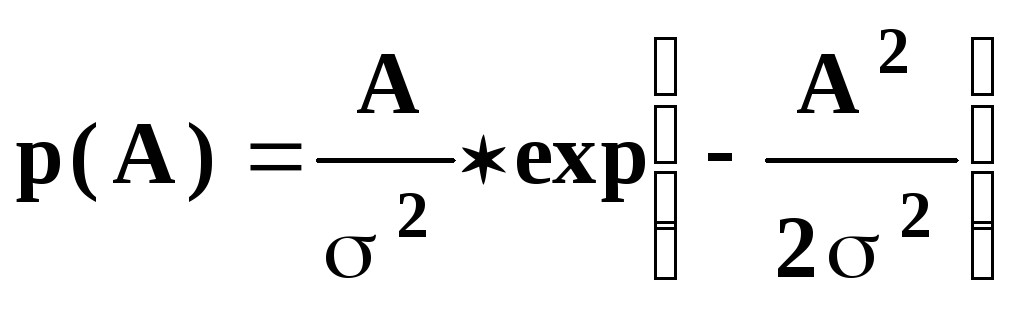t0 = 2 мксек: j0- случайная начальная фаза, распределенная по закону:
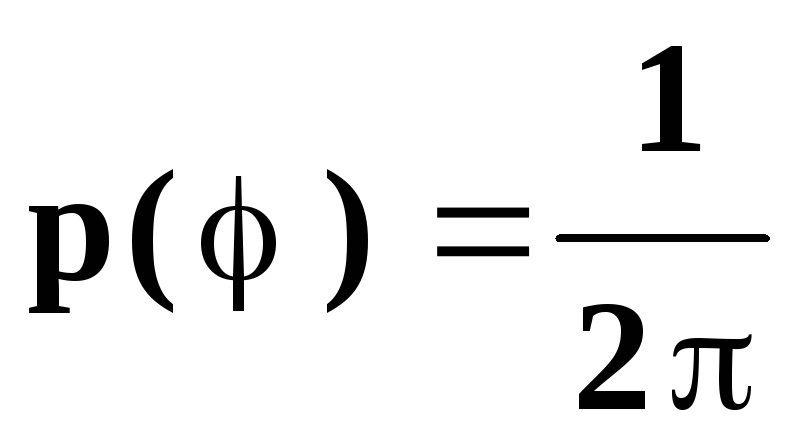
n(t) - квазибелый гауссовский шум, имеющий спектральную плотность:
S(w)=N0/2
в полосе |Dw| = w2 - w1, полностью перекрывающей спектр сигнала.
w0=2pf0; f0 = 5*106 Гц; |Dw| = 2p*5*106
Требуется определить:
А.Структуру согласованного фильтра и параметры (ширина полосы пропускания и изменение отношения сигнал/помеха на выходе по сравнению со входом) квазиоптимального фильтра, состоящего из 1 колебательного контура.
В.Зависимость PD(d), где d2=ss2/sn2 на входе приемного тракта, если обнаружитель выполнен по схеме согласованный фильтр - линейный детектор - пороговое устройство. Результаты сравнить с работой простейшего обнаружителя Неймана-Пирсона. При этом с доверительной вероятностью P=0.9 должно быть не более n0=0 ложного срабатывания регистратора в N0=105 независимых точках анализа.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
1,2402 |
1,4203 |
0,8805 |
2,3142 |
2,9578 |
2,7186 |
3,6362 |
3,0507 |
3,139 |
2,0481 |
|
|
2 |
0,9805 |
1,667 |
1,4365 |
3,3057 |
3,7471 |
1,8715 |
1,3067 |
0,9667 |
0,6064 |
-0,129 |
|
|
3 |
2,3222 |
2,3396 |
1,4161 |
1,4681 |
0,8049 |
0,1564 |
0,4022 |
1,3881 |
1,527 |
0,5216 |
|
|
4 |
-4,856 |
-2,578 |
-3,206 |
-4,042 |
-3,15 |
-1,896 |
-2,034 |
-0,312 |
-0,133 |
-0,45 |
|
|
5 |
-1,813 |
-1,412 |
-2,599 |
-2,531 |
-0,824 |
-0,263 |
-0,713 |
0,1842 |
-0,221 |
-0,549 |
|
|
6 |
0,0525 |
0,4179 |
0,2664 |
1,0659 |
0,7268 |
-0,518 |
-2,028 |
-0,433 |
-0,094 |
0,0172 |
|
|
7 |
-2,37 |
-0,884 |
-1,371 |
-1,889 |
-2,469 |
-1,013 |
-1,963 |
-0,866 |
-1,286 |
-2,095 |
|
|
8 |
5,3123 |
3,6493 |
3,4355 |
5,3657 |
5,6881 |
4,3849 |
5,1384 |
2,8661 |
2,5443 |
1,7372 |
|
|
9 |
-1,567 |
-1,273 |
-3,164 |
-5,444 |
-5,726 |
-3,824 |
-4,946 |
-2,073 |
-1,948 |
-1,839 |
|
|
10 |
6,4554 |
3,7843 |
2,939 |
4,4628 |
4,7661 |
3,0075 |
3,009 |
2,0304 |
1,5457 |
0,668 |
|
|
11 |
3,744 |
2,4344 |
2,2228 |
3,8499 |
3,961 |
3,1928 |
3,551 |
2,5776 |
2,5753 |
1,7625 |
|
|
12 |
-0,222 |
0,3119 |
-0,48 |
-0,045 |
-0,378 |
-0,275 |
-1,392 |
-0,155 |
-0,083 |
-0,44 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
1 |
4,7286 |
2,2937 |
3,0692 |
3,5345 |
2,2397 |
4,8558 |
5,9748 |
3,2524 |
4,0553 |
4,3319 |
7,0796 |
|
2 |
-0,675 |
0,5795 |
0,4501 |
0,5399 |
-0,091 |
0,1919 |
0,6606 |
-0,116 |
0,4473 |
-1,386 |
-2,273 |
|
3 |
0,6613 |
0,9271 |
1,1081 |
1,3898 |
0,5996 |
0,7753 |
0,115 |
-0,468 |
0,2881 |
-0,327 |
0,1168 |
|
4 |
-1,401 |
0,0875 |
-0,976 |
-1,461 |
-1,407 |
-1,73 |
-1,705 |
-1,478 |
-0,687 |
-1,679 |
-1,534 |
|
5 |
-1,663 |
0,2708 |
0,7035 |
0,9718 |
-0,068 |
0,1641 |
-0,168 |
-0,706 |
-0,215 |
-0,725 |
-0,708 |
|
6 |
0,2927 |
0,799 |
1,0032 |
1,246 |
0,6541 |
2,2878 |
2,5756 |
0,8242 |
1,393 |
1,6364 |
3,5106 |
|
7 |
-4,279 |
-0,782 |
-1,406 |
-1,519 |
-1,121 |
-1,063 |
-1,555 |
-1,036 |
-0,629 |
-0,906 |
-2,069 |
|
8 |
5,136 |
2,9236 |
3,2877 |
3,4908 |
2,1362 |
4,0158 |
4,1433 |
1,7089 |
2,7285 |
2,7825 |
6,2115 |
|
9 |
-3,465 |
-0,257 |
-0,736 |
-0,831 |
-0,961 |
-0,731 |
-0,274 |
-0,535 |
-0,096 |
-1,542 |
-2,741 |
|
10 |
0,2912 |
0,4913 |
0,1281 |
-0,038 |
-0,527 |
0,213 |
0,829 |
0,145 |
0,8959 |
0,69 |
1,9334 |
|
11 |
4,1204 |
1,9003 |
1,9897 |
1,8554 |
0,8749 |
2,279 |
1,8095 |
0,0958 |
-0,124 |
-0,958 |
-2,59 |
|
12 |
-0,315 |
0,4748 |
0,3016 |
-0,468 |
-1,446 |
-2,424 |
-2,546 |
-1,211 |
-0,593 |
-1,155 |
-2,66 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение параметров случайного процесса
1.1. Нахождение математического ожидания и дисперсии случайного процесса Математическое ожидание и дисперсия случайного процесса X(t) в дискретные моменты времени будут задаваться следующими формулами
,
где
–математическое
ожидание,
–дисперсия.
Мат ожидание
|
0,7733 |
0,8233 |
0,1481 |
0,6567 |
0,8421 |
0,6286 |
0,3305 |
0,7688 |
0,6811 |
0,1044 |
0,286 |
|
0,809 |
0,7437 |
0,7259 |
0,0735 |
0,7361 |
0,8217 |
0,0397 |
0,6219 |
0,0636 |
0,3565 |
Дисперсия
|
10,874 |
4,2738 |
5,3802 |
12,171 |
12,35 |
5,8456 |
9,1699 |
2,6769 |
2,5467 |
1,7629 |
9,1764 |
|
1,1477 |
2,1873 |
2,8974 |
1,601 |
4,9889 |
6,1559 |
1,8119 |
2,1423 |
3,676 |
12,441 |
СКО
|
3,2976 |
2,0673 |
2,3195 |
3,4887 |
3,5142 |
2,4178 |
3,0282 |
1,6361 |
1,5958 |
1,3277 |
3,0293 |
|
1,0713 |
1,4789 |
1,7022 |
1,2653 |
2,2336 |
2,4811 |
1,3461 |
1,4637 |
1,9173 |
3,5271 |
1.2. Нахождение корреляционной матрицы случайного процесса
Корреляционная матрица случайного процесса X(t) будет находится из корреляционных моментов сечений процесса X(t) в дискретные моменты времени по формуле:
Корреляционная Матрица
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
1 |
10,87 |
6,66 |
7,14 |
10,22 |
9,91 |
6,59 |
7,95 |
4,12 |
3,82 |
3,08 |
6,74 |
2,29 |
3,05 |
3,37 |
2,37 |
4,08 |
4,39 |
2,26 |
2,34 |
2,97 |
5,27 |
|
2 |
6,66 |
4,27 |
4,70 |
6,78 |
6,49 |
4,27 |
5,16 |
2,70 |
2,54 |
2,00 |
4,40 |
1,50 |
1,99 |
2,21 |
1,58 |
2,64 |
2,82 |
1,49 |
1,57 |
1,94 |
3,42 |
|
3 |
7,14 |
4,70 |
5,38 |
7,95 |
7,65 |
5,04 |
6,03 |
3,13 |
2,96 |
2,35 |
5,20 |
1,76 |
2,31 |
2,55 |
1,86 |
3,14 |
3,31 |
1,72 |
1,80 |
2,28 |
4,02 |
|
4 |
10,22 |
6,78 |
7,95 |
12,17 |
12,02 |
7,96 |
9,45 |
4,90 |
4,60 |
3,69 |
8,12 |
2,73 |
3,65 |
4,02 |
2,88 |
4,87 |
5,20 |
2,72 |
2,83 |
3,57 |
6,26 |
|
5 |
9,91 |
6,49 |
7,65 |
12,02 |
12,35 |
8,28 |
9,95 |
5,16 |
4,80 |
3,89 |
8,41 |
2,85 |
3,83 |
4,24 |
2,99 |
5,08 |
5,49 |
2,83 |
2,96 |
3,69 |
6,64 |
|
6 |
6,59 |
4,27 |
5,04 |
7,96 |
8,28 |
5,85 |
7,20 |
3,73 |
3,45 |
2,74 |
6,06 |
2,07 |
2,75 |
3,02 |
2,14 |
3,66 |
3,91 |
2,04 |
2,12 |
2,68 |
4,70 |
|
7 |
7,95 |
5,16 |
6,03 |
9,45 |
9,95 |
7,20 |
9,17 |
4,86 |
4,54 |
3,58 |
7,89 |
2,70 |
3,55 |
3,92 |
2,82 |
4,77 |
5,08 |
2,65 |
2,77 |
3,47 |
6,16 |
|
8 |
4,12 |
2,70 |
3,13 |
4,90 |
5,16 |
3,73 |
4,86 |
2,68 |
2,57 |
2,04 |
4,45 |
1,50 |
2,00 |
2,22 |
1,59 |
2,68 |
2,85 |
1,49 |
1,56 |
1,96 |
3,46 |
|
9 |
3,82 |
2,54 |
2,96 |
4,60 |
4,80 |
3,45 |
4,54 |
2,57 |
2,55 |
2,07 |
4,55 |
1,52 |
2,03 |
2,25 |
1,61 |
2,72 |
2,90 |
1,52 |
1,58 |
1,99 |
3,50 |
|
10 |
3,08 |
2,00 |
2,35 |
3,69 |
3,89 |
2,74 |
3,58 |
2,04 |
2,07 |
1,76 |
3,92 |
1,33 |
1,77 |
1,94 |
1,38 |
2,36 |
2,54 |
1,31 |
1,36 |
1,71 |
3,06 |
|
11 |
6,74 |
4,40 |
5,20 |
8,12 |
8,41 |
6,06 |
7,89 |
4,45 |
4,55 |
3,92 |
9,18 |
3,18 |
4,23 |
4,61 |
3,28 |
5,60 |
5,99 |
3,13 |
3,24 |
4,10 |
7,20 |
|
12 |
2,29 |
1,50 |
1,76 |
2,73 |
2,85 |
2,07 |
2,70 |
1,50 |
1,52 |
1,33 |
3,18 |
1,15 |
1,54 |
1,70 |
1,22 |
2,05 |
2,19 |
1,14 |
1,20 |
1,49 |
2,66 |
|
13 |
3,05 |
1,99 |
2,31 |
3,65 |
3,83 |
2,75 |
3,55 |
2,00 |
2,03 |
1,77 |
4,23 |
1,54 |
2,19 |
2,48 |
1,76 |
2,95 |
3,14 |
1,65 |
1,72 |
2,17 |
3,80 |
|
14 |
3,37 |
2,21 |
2,55 |
4,02 |
4,24 |
3,02 |
3,92 |
2,22 |
2,25 |
1,94 |
4,61 |
1,70 |
2,48 |
2,90 |
2,10 |
3,55 |
3,78 |
1,97 |
2,06 |
2,59 |
4,57 |
|
15 |
2,37 |
1,58 |
1,86 |
2,88 |
2,99 |
2,14 |
2,82 |
1,59 |
1,61 |
1,38 |
3,28 |
1,22 |
1,76 |
2,10 |
1,60 |
2,77 |
2,95 |
1,52 |
1,59 |
2,00 |
3,56 |
|
16 |
4,08 |
2,64 |
3,14 |
4,87 |
5,08 |
3,66 |
4,77 |
2,68 |
2,72 |
2,36 |
5,60 |
2,05 |
2,95 |
3,55 |
2,77 |
4,99 |
5,43 |
2,81 |
2,90 |
3,68 |
6,51 |
|
17 |
4,38 |
2,82 |
3,31 |
5,20 |
5,49 |
3,91 |
5,08 |
2,85 |
2,90 |
2,54 |
5,99 |
2,19 |
3,14 |
3,78 |
2,95 |
5,43 |
6,16 |
3,26 |
3,41 |
4,24 |
7,50 |
|
18 |
2,26 |
1,48 |
1,72 |
2,72 |
2,83 |
2,04 |
2,65 |
1,49 |
1,52 |
1,31 |
3,13 |
1,14 |
1,65 |
1,97 |
1,52 |
2,81 |
3,26 |
1,81 |
1,93 |
2,42 |
3,85 |
|
19 |
2,34 |
1,57 |
1,80 |
2,83 |
2,96 |
2,12 |
2,77 |
1,56 |
1,58 |
1,36 |
3,24 |
1,20 |
1,72 |
2,06 |
1,59 |
2,90 |
3,41 |
1,93 |
2,14 |
2,70 |
4,85 |
|
20 |
2,97 |
1,94 |
2,28 |
3,57 |
3,69 |
2,68 |
3,47 |
1,96 |
1,99 |
1,71 |
4,10 |
1,49 |
2,17 |
2,59 |
2,00 |
3,68 |
4,24 |
2,42 |
2,70 |
3,68 |
6,60 |
|
21 |
5,27 |
3,42 |
4,02 |
6,26 |
6,63 |
4,70 |
6,16 |
3,46 |
3,50 |
3,06 |
7,20 |
2,66 |
3,80 |
4,57 |
3,56 |
6,51 |
7,50 |
4,20 |
4,85 |
6,60 |
12,44 |