16. Теорема о конечности симплекс-алгоритма (без доказательства).

Если существует оптимальное решение задачи линейного программирования, то существует и базисное оптимальное решение. Последнее всегда может быть получено с помощью симплекс-метода, причем начинать можно с любого исходного базиса.

Эту теорему часто называют теоремой о конечности симплекс-алгоритма. И, действительно, в ней утверждается, что если ЗЛП разрешима, то, взяв любой исходный базис и выбирая последовательность разрешающихся элементов подходящим образом, мы всегда придем – после конечного числа шагов – к базисному оптимальному решению.

17. Постановка взаимно-двойственных задач.

Задача 1.

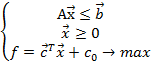
Задача 2

Столбцы неотрицательных неизвестных

; ẍ=(x₁,x₂,…,x_n)^T≥0

ŷ=(y₁,y₂,…,y_n)^T≥0

ᵬ

Столбцы правых частей

=(b₁,b₂,…,b_n)^T

ĉ=(c₁,c₂,…,c_n

18. Основное неравенство для двойственных задач (с доказательством). Достаточный признак оптимальности.

Пусть Х – какое–нибудь допустимое решение задачи 1, а У – какое-нибудь допустимое решение задачи 2. Тогда f(X)≤φ(Y)

Доказательство: т.к. Аẍ≤ᵬ => (Аẍ)^Т≤ᵬ^Т => ẍ^ТА^Т≤ᵬ │*У≥0 => ẍ^ТА^Тŷ≤ᵬ^Тŷ => ẍ(А^Тŷ)≤ᵬ^Тŷ=φ(ŷ)-c₀

Аналогично: А^Тŷ≥ĉ│*ẍ^т≥0 => ẍ^Т(А^тŷ)≥ẍ^тĉ=f(ẍ)-c₀

Отсюда: f(X)≤ ẍ^Т(А^тŷ)+c₀≤φ(Y) => f(X)≤φ(Y) ЧТД

Если для каких –то допустимых решений ẍ^* и ŷ^* задач 1 и 2 выполняется равенство f(ẍ)=φ(ŷ), то ẍ^* и ŷ^* - оптимальные решения задач 1 и 2 соответственно.

19. Основная теорема двойственности. Критерий оптимальности (без доказательства).

Если исходная задача имеет оптимальное решение, то и двойственная ей так же имеет оптимальное решение. При этом оптимальные значения целевых функций равны: f_max=φ_min.

ẍ^*ϵD₁ оптимален ˂=>существует решение ŷ^*ϵD₂, такое, что ĉ^Тẍ^*=ᵬ^Тŷ^*

20. Теорема равновесия (с доказательством).

Оптимальные решения ẍ^*=(х₁^*,х₂^*,…х_n^*)^Т и ŷ^*=(у₁^*,у₂^*,…,у_n^*) пары двойственных задач связаны следующим соотношением:

(1)

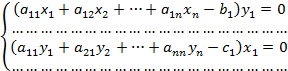
Д оказательство: Из критерия оптимальности => f(ẍ) = φ(ŷ) => ẍ^ТА^Тŷ=f(ẍ)

ẍ^TA^Tŷ=φ(ŷ)

Пусть задача 1 имеет размеры m*n

Где iϵ[1;m], jϵ[1;n]

x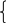 ₁(

y₁(

Что и записано в системе (1). ЧТД

21. Постановка транспортной задачи (тз).

Транспортная задача была впервые сформулированна Хитчкоком.

Транспортная задача — задача линейного программирования, в которой требуется найти оптимальный план транспортировки (однородного) продукта из конечного числа пунктов поставки с заданными объемами производства в конечное число пунктов потребления с известными объемами потребностей при заданной стоимости перевозки единицы транспортируемого продукта между каждой парой пунктов поставки и потребления.

Таким образом, оптимальный план должен определять минимальную суммарную стоимость транспортировки, не превышая объем производства каждого из поставщиков и полностью покрывая потребности каждого из потребителей.

Математическая модель может быть описана следующим образом. Пусть имеются m поставщиков A₁,A₂,...,A_m и n потребителей B₁,B₂,...,B_n некоторого однородного продукта. Для i-го поставщика задан объем производства a_i ≥ 0 (i= (1;m)), а для j-го потребителя — объем потребления b_j ≥0 (j= (1;n)) и известна стоимость доставки единицы продукта c_ij≥0 из пункта производства i в пункт потребления j. Переменные x_ij≥0 характеризуют объем первозки между i-м поставщиком и j-м потребителем. Оптимальный план транспортировки соответствует минимуму линейной целевой функции

F(X) = ^m_i=1∑ⁿ_j=1∑c_ij x_ij→min при ограничениях на потребление и поставку ^m_i=1∑x_ij=b_j , ⁿ_j=1∑x_ij=a_i . Число базисных переменных в системе ограничений равно m+n-1.

Данные обычно представляют в виде транспортной таблицы:

Поставщики	Потребители				Запасы
	B1	B2	...	Bn
A1	С11 x11	С12 x12	...	С1n x1n	a1
A2	С21 x21	С22 x22	...	С23 x23	a2
...	...	...	...	...	...
Am	Сm1 xm1	Сm2 xm2	...	Сmn xmn	an
Потребности	b1	b2	...	bn