6.2. Тема 2. Наилучшее среднеквадратическое приближение. Тригонометрическая интерполяция. Наилучшее равномерное приближение Задание 1
Дана функция
.
Разложить эту функцию в тригонометрический
ряд Фурье
на
.
Изобразить график периодического (с
периодом
)
продолжения функции
и график суммы ряда Фурье.
Построить (с помощью Excel,
например) на одном чертеже график функции
и график
,
наилучшего среднеквадратического
приближения для функции
на
в множестве тригонометрических
многочленов n-ой
степени
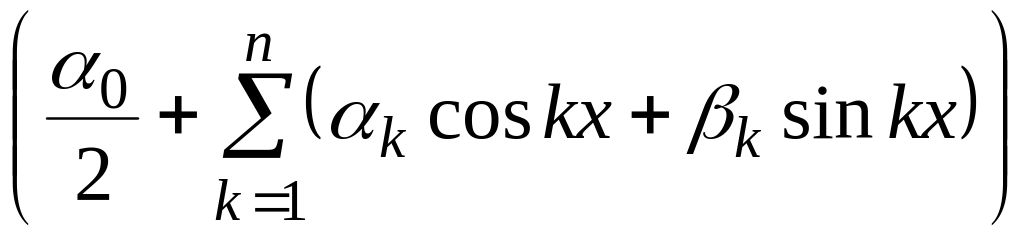при следующих значениях n:
1, 10, 50. Пронаблюдать явление Гиббса.
Варианты для выполнения задания 1 взять
из табл. 2.1.
Задание 2
Дана таблица
значений,
,
некоторой функции
в точках
,
.
Значения
приближенные и имеют значительные
погрешности.
Получить (используя,
например, Excel)
наилучшее среднеквадратическое
приближение для функции
в семействе линейных функций
(найти a
и b)
методом наименьших квадратов, построить
его график, показать на нем табличные
точки
.
Задание 3
Дана таблица
значений
,
некоторой функции
в точках
,
.
Значения
имеют значительные погрешности.
Для построения
наилучшего среднеквадратического
приближения функции
методом наименьших квадратов подобрать
наиболее подходящее параметрическое
семейство функций среди следующих
семейств нелинейных функций:
,
,
,
,
,
.
Получить (используя,
например, Excel)
наилучшее среднеквадратическое
приближение
функции
в выбранном семействе нелинейных функций
(вычислить коэффициенты a
и b),
а также построить график этого приближения,
показать на нем табличные точки
.
Таблица 2.1
№ варианта |
|
17 |
|
Задание 4
Определить какое
из двух, полученных при выполнении
предыдущих заданий, приближений
или
является лучшим?
Варианты для выполнения заданий 2 4 взять из табл. 2.2.
Таблица 2.2
№ вар-та |
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
17 |
|
1.01 |
1.74 |
2.38 |
3.02 |
3.66 |
4.30 |
4.94 |
5.18 |
|
-1.73 |
-2.98 |
-3.53 |
-3.89 |
-4.01 |
-4.25 |
-4.32 |
-4.38 |
6.3. Тема 3. Численное дифференцирование. Метод
Рунге-Ромберга
Задание 1
Построить (используя,
например, табличный процессор Excel)
таблицы значений функции
,
а также ее первой производной
(предварительно вычисленной аналитически)
на сетке с узлами
(
,
).
В табличных значениях сохранять 10 знаков
после десятичной запятой. Эти таблицы
использовать при выполнении заданий
2, 3, 4.
Задание 2
Используя формулу
численного дифференцирования
и построенную при выполнении предыдущего
задания таблицу значений функции
(с помощью, например, табличного процессора
Excel),
получить таблицу приближенных значений
первой производной и абсолютной
погрешности этих значений в точках
(
,
).
Задание 3
Используя ту же
формулу численного дифференцирования
,
только с удвоенным шагом, и построенную
при выполнении первого задания таблицу
значений функции
(с помощью, например, табличного процессора
Excel)
получить таблицу приближенных значений
первой производной и значений ее
абсолютной погрешности в точках
(
,
).
Задание 4
На основе таблиц приближенных значений первой производной, полученных при выполнении заданий 2 и 3, составить таблицу значений асимптотической оценки погрешности приближенного значения первой производной (см. метод Рунге-Ромберга), полученного в задании 2. Сопоставить значения асимптотической оценки погрешности и точные значения погрешности. Сделать выводы из этого сопоставления.
Варианты для заданий 1 – 4 взять из табл. 3.1.
Таблица 3.1
№ вар-та |
|
17 |
|
