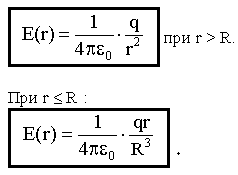- •Билет №1
- •Билет №2
- •Билет №3
- •Билет №4
- •Билет №5
- •1)Равнопеременное вращательное движение. Связь линейных величин с угловыми.
- •Билет №6
- •1)Свободное падение тел. Ускорение свободного падения. Движение тела, брошенного под углом к горизонту.
- •Билет №7
- •1)Первый, второй третий законы Ньютона. Инерциальная система отсчета.
- •Билет №8
- •.Динамика вращательного движения. Основное уравнение динамики вращательного движения. Момент инерции тела. Момент импульса.
- •2)Электрическое поле. Напряженность электрического поля. Теорема Гаусса.
- •Билет №10
- •1)Силы в природе. Сила всемирного тяготения. Гравитационная постоянная. Сила тяжести. Движение искусственных спутников. Первая космическая скорость.
- •Билет №11
- •1)Вес тела. Невесомость и перегрузки. Вес тела, движущегося с ускорением.
- •Билет № 12
- •1)Сила трения. Природа силы трения. Роль силы трения.
- •Билет №13
- •1)Импульс тела. Импульс силы. Изменение импульса системы взаимодействующих тел. Закон сохранения импульса.
- •8.314472 - Универсальная газовая постоянная численно равна работе 1 моля идеального газа при изобарном нагревании на 1 к.
- •Билет №14
- •1)Работа силы. Кинетическая энергия. Теорема о кинетической энергии.
- •Билет №15
- •1)Работа силы тяжести. Потенциальная энергия тела, поднятого над поверхностью Земли. Потенциальная энергия тела в гравитационном поле.
- •Билет №16
- •1)Работа силы упругости. Потенциальная энергия деформированной пружины.
- •Билет №17
- •1)Полная энергия тела. Изменение энергии системы тел под действием внешних сил. Закон сохранения полной механической энергии.
- •Билет №18
- •1)Механическая работа и мощность. Кпд (на примере наклонной плоскости).
- •Билет №19
- •1)Равновесие твердых тел при отсутствии вращения. Условие равновесия тела с закрепленной осью вращения. Момент силы. Условие равновесия твердого тела.
- •2) Основное уравнение мкт газов.
- •Билет №20
- •1)Передача давления газами и жидкостями. Закон Паскаля. Действие жидкостей газов на погруженное в него тело. Сила Архимеда и причины её возникновения. Условие плавания тела.
Билет №1
1)Механическое движение. Относительность механического движения. Поступательное движение тела. Материальная точка. Положение тела в пространстве. Система отсчета. Перемещение. Закон сложения скоростей в классической механике.
Основная задача механики – определить координату и скорость тела в любой момент времени по известным начальным координате и скорости. Основную задачу механики напрямую решает кинематика – раздел механики, изучающий способы описания движения.
Механическое движение – это изменение положения тела в пространстве относительно других тел.
Относительность движения наиболее просто продемонстрировать на примерах:
Человек идёт по вагону движущегося поезда к проводнику за чаем . Медленно идёт (вагон качается). Его скорость 1-2 м/с. Но! Относительно поезда. Относительно земли его скорость равна скорости поезда ± его скорость относительно поезда, то есть около 20-30 м/с. Естественно, за то время, за которое человек пройдёт длину вагона относительно земли он переместиться за несколько километров.
Как движется, парящий внутри космической станции космонавт? Неподвижен относительно станции и несётся с первой космической скоростью по окружности вокруг Земли.
Таким образом, мы можем утверждать, что большинство характеристик движения (скорость, перемещение, траектория, путь) относительны и имеют различное значение в разных системах отсчёта.
В механике рассматриваются два разных типа движения: поступательное (рис. 1) и вращательное (рис.2).
Поступательным называется движение, при котором все точки тела движутся по одинаковым траекториям. При вращательном движении различные точки тела движутся по разным траекториям.
П
 ри
поступательном движении достаточно
определить характер движения одной
(любой точки), чтобы определить характер
движения всего тела. В этом случае тело
можно считать материальной
точкой –
объектом,
размерами которого можно пренебречь в
условиях данной задачи.
Материальной точкой можно считать тело
не только при поступательном движении,
но и при перемещении тела на расстояния
много большие чем размеры самого тела.
Например, корабль, плывущий вокруг
Земли, совершает вращательное движение,
но может считаться материальной точкой.
ри
поступательном движении достаточно
определить характер движения одной
(любой точки), чтобы определить характер
движения всего тела. В этом случае тело
можно считать материальной
точкой –
объектом,
размерами которого можно пренебречь в
условиях данной задачи.
Материальной точкой можно считать тело
не только при поступательном движении,
но и при перемещении тела на расстояния
много большие чем размеры самого тела.
Например, корабль, плывущий вокруг
Земли, совершает вращательное движение,
но может считаться материальной точкой.
Как и движение, положение тела в пространстве относительно и задаётся по отношению к некому выбранному предмету – телу отсчёта. Для указания положения тел и направления их перемещения служат системы координат. И, наконец, для измерения скорости движения тела нужен измеритель времени – часы. Тело отсчёта, система координат и часы определяют систему отсчёта (рис. 3). Когда задана система отсчёта, можно определить путь и перемещение. Траектория – множество точек, которые проходит тело в процессе своего движения. Путь (L) – длина траектории (скалярная величина). Перемещение (S) – вектор, соединяющий начальное и конечное положение тела. [L] = 1 м, [S] = 1 м.
Р ассмотрим
две системы отсчёта: одна неподвижная
(XYZ)
(предположим, связанная с берегом),
другая (X’Y’Z’)
(например, связанная с кораблём) движется
относительно первой со скоростью Vo
(рис. 4). Тогда, если перемещение тела в
подвижной системе отсчёта S’,
а перемещение самой системы отсчёта
So,
то перемещение тела относительно
неподвижной системы равно:
ассмотрим
две системы отсчёта: одна неподвижная
(XYZ)
(предположим, связанная с берегом),
другая (X’Y’Z’)
(например, связанная с кораблём) движется
относительно первой со скоростью Vo
(рис. 4). Тогда, если перемещение тела в
подвижной системе отсчёта S’,
а перемещение самой системы отсчёта
So,
то перемещение тела относительно
неподвижной системы равно:

![]()
Если поделить это перемещение на время, за которое оно
произошло, то получим закон преобразования скоростей:
![]() +
+![]()
2) Напряженность электрического поля точечного заряда, проводящего шара, нити, плоскости.
Применение теоремы Гаусса для вычисления полей. Теорема Гаусса:
![]() S - любая замкнутая поверхность,
S - любая замкнутая поверхность,
![]() -
сумма зарядов внутри S.
Поле
равномерно заряженной бесконечной
плоскости
-
сумма зарядов внутри S.
Поле
равномерно заряженной бесконечной
плоскости
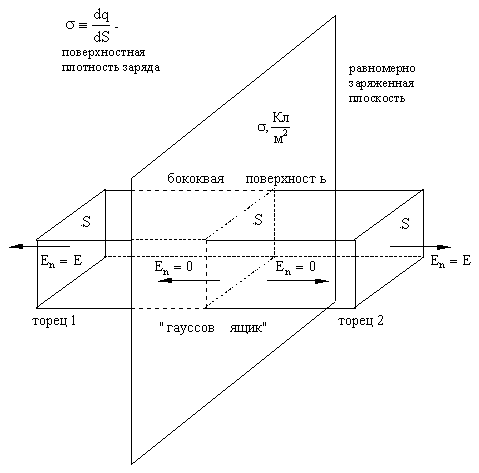
Введём понятие поверхностной плотности заряда
![]() если поверхность бесконечна и равномерно
заряжена, тогда
если поверхность бесконечна и равномерно
заряжена, тогда ![]() – одинакова и линия Е перпендикулярна
плоскости в любой точке.
– одинакова и линия Е перпендикулярна
плоскости в любой точке.
Мысленно представим в пространстве «ящик».
Считаем Σqi внутри "гауссова ящика": очевидно,
;![]()
И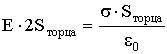 так:
так:
В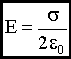 ыражаем
E:
ыражаем
E:
.
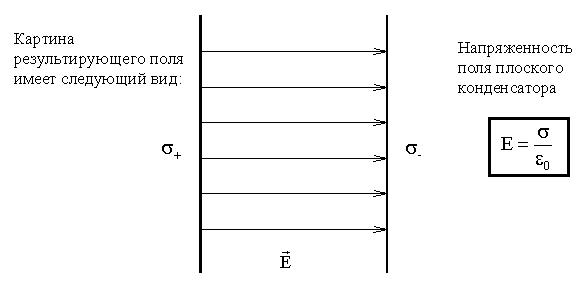
Поле равномерно заряженной бесконечной плоскости однородно.
П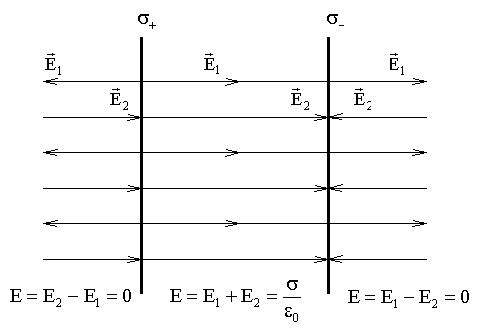 оле
плоского конденсатора
оле
плоского конденсатора
![]() .
Т.к.
.
Т.к. ![]() ,
,
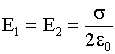 .
.
Поле однородно заряженного бесконечного цилиндра
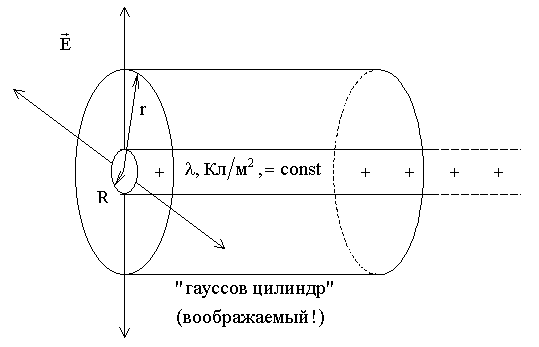
![]() -
линейная плотность заряда.
-
линейная плотность заряда.
Весь
поток вектора напряженности будет
выходить через боковую поверхность
цилиндра, ![]() ,
,
Отсюда:
![]() Применяя
теорему Гаусса, получим:
Применяя
теорему Гаусса, получим:
![]() ,
при r > R.
,
при r > R.
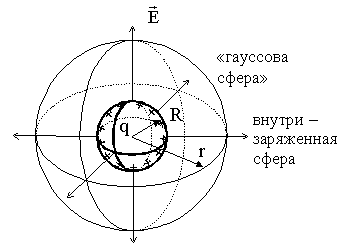
Поле однородно заряженной сферы
|
Применяя теорему Гаусса, получим:
при
r > R.
Если r < R, то |
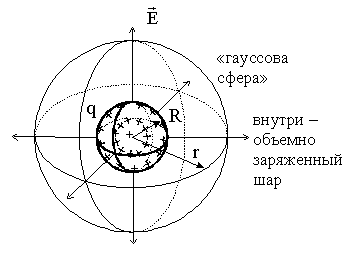
Поле объемного
заряженного шара
![]() -
объемная плотность заряда
q- суммарный
заряд шара
-
объемная плотность заряда
q- суммарный
заряд шара
|
Применяя теорему Гаусса, получим:
|