1.4 Расчет теоретической и полной длин стрелочного перевода

Теоретическую длину стрелочного перевода L_т находят по формуле:

L_т = R (sin-sin_н) + kcos. (1.18)

L_т=495888*(0,076695 -0,021233) + 2232*0,997055 = 29728 мм.

Полная (практическая) длина стрелочного перевода:

L_П=q + L_т + m, (1.19)

L_П = 2919+ 29728+ 2964 = 35611 мм.

Осевые размеры стрелочного перевода (рисунок 1.6) определяют по формулам:

b₀ = S₀/(2 tg /2), (1.20)

a₀ = L_т - b₀, (1.21)

a = a₀ + q, (1.22)

b = b₀ + m. (1.23)

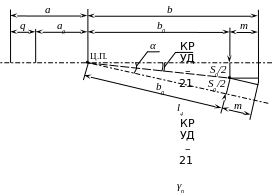
Рисунок 1.6-Осевые размеры стрелочного перевода

b₀ = 1520/(2*0,038404) = 19790 мм;

a₀ = 29728 – 19790 = 9938 мм;

a = 9938 + 2919 = 12857 мм;

b = 19790 + 2964 = 22754 мм.

1.5 Расчет ординат переводной кривой

Ординаты переводной кривой определяют следующим образом (рисунок 1.7). Начало координат располагают по рабочей грани рамного рельса против корневого стыка остряка и отсюда откладывают абсциссы x через каждые 2000 мм, вычисляя соответствующие им ординаты y.

Принимается: х₁ = 2000мм; х₂ = 4000 мм; … , х_n = 2000n мм; x_k .

Конечная абсцисса находится по формуле:

x_k=R (sin - sin) (1.24)

x_k = 495888*(0,076695 - 0,033212) = 21563 мм.

Ординаты переводной кривой определяются по формуле:

y_n = y₀ + x_n sin  + x_п²/(2R) +, (1.25)

где y₀ - ордината в корне остряка, мм;

x_n - абсциссы переводной кривой, кратные 2000 мм;

y_n - ординаты переводной кривой, соответствующие своим абсциссам,

мм;

 - стрелочный угол, доли град.;

 - поправка для соответствующей ординаты;

 = (Rsin + x_n) ⁴/(8R³). (1.26)

Величина  вначале определяется для конечной абсциссы x_к по формуле:

_к = (Rsin + x_к)⁴/ (8R³). (1.27)

_к=(495888*0,033212 +21563)⁴/(8*(495888)³) = 2,14 мм.

Если для конечной абсциссы величина поправки _к не превышает 1 мм, то ее можно не учитывать и для остальных ординат не определять. В случае, когда эта величина превышает 1 мм, то она определяется для x_n , x_n-1 и т.д., пока ее значение не окажется меньше миллиметра. Для остальных ординат поправки  можно не определять.

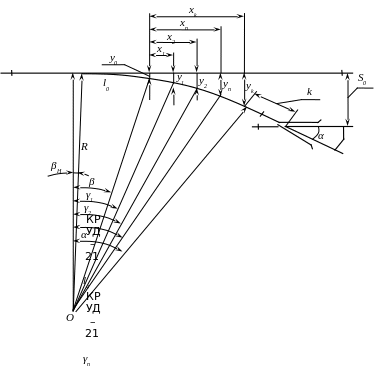
Рисунок 1.7- Расчетная схема ординат переводной кривой

Расчет ординат сводят в таблицу 1.2

Таблица 1.2 – Расчет ординат переводной кривой

xn	y0	xnsinβ	xn2/(2R)		y
2000	162	66	4	0	232
4000		133	16	0	311
6000		199	36	0	397
8000		266	64	0	492
10000		332	101	0	595
12000		399	145	1	707
14000		465	198	1	826
16000		531	258	1	952
18000		598	327	2	1089
20000		664	403	2	1231
21563		716	469	2	1349

Конечная ордината проверяется по формуле:

y_k = S₀ – ksinα. (1.28)

y_k = 1520 – 2232*0,076695 = 1349 мм.

Сравниваются значения y_k рассчитанные по формулам (1.25) и (1.28).

Разница между ними не должна превышать 3 мм.