6.2.4.2. Приближение свободных электронов. Энергетический спектр электронов в прямоугольной потенциальной яме.

В приближении свободных электронов потенциал решетки считается постоянным. Поэтому с энергетической точки зрения кристалл в этом случае представляет собой одиночную потенциальную яму с гладким дном. Действительно, вне кристалла потенциальная энергия свободного электрона U = 0, а внутри кристалла U₀ = -q₀, где ₀ – положительный постоянный потенциал поля, созданного узлами решетки. Электрон не может свободно покинуть кристалл. Для выхода из него электрону необходимо совершить работу, численно равную U_o.

Характер энергетического спектра электронов в кристалле (в потен-циальной яме) обсудим на примере одномерной модели, поскольку для выяснения важнейших особенностей энергетического спектра одномерного случая вполне достаточно, Напомним, что для его нахождения нам нужно решить одноэлектронное уравнение Шредингера (6.2.1), которое в одномерном случае имеет вид :

(6.2.18)

Решим это уравнение для двух типов потенциальной энергии, показанных на рис. 6.2.2. Случай, когда U(x) = 0 при –a < x < a и U(x) = +. при | x | > a, что соответствует бесконечно высоким стенкам прямоугольной потенциальной ямы, расположенным в точках х =± a, показан на рис. 6.2,а. Потенциальная энергия, изображенная на рис. 6.2,б, изменяется у стенки скачкообразно, но на конечную величину, так что при | x | > а U(x) = U₀. Для обоих типов потенциальной энергии движение классической частицы с полной энергией Е < U₀ будет одним и тем же но, как мы увидим, ее квантово-механическое поведение оказывается различным .

Б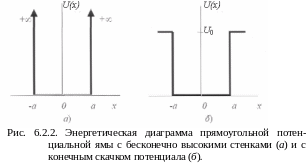 есконечно высокие стенки. Внутри потенциальной ямы (при | x | < а) волновое уравнение (6.2.18) записывается в виде

(6.2.19)

и его общее решение есть

, (6.2.20)

Выбирая в качестве граничного условия обращение в нуль волновой функции в точках х = ± а, получаем

Откуда

Решение, для которого константы: А и В равны нулю, не представляют физического интереса, так как при этом ψ = 0 в любой точке. Нельзя также одновременно приравнять нулю sinαa и соsαa при одном и том же значении α (т. е. E). Поэтому имеется два возможных класса решений. Для первого класса

A = 0 соsαa = 0

а для второго класса

В = 0 sinαa = 0.

Таким образом, aa = nπ / 2 где для первого класса п – нечетное, а для второго класса – четное число. Следовательно, собственные функции обоих классов и принадлежащие им собственные значения энергии имеют вид

, где n нечетное;

, где n четное;

в обоих случаях

Ясно, что при n = 0 получается физически неинтересное решение ψ = 0, а решения с отрицательными и положительными значениями п линейно связаны друг с другом. Константы А и В легко находятся из условия нормировки собственных функций ψ(х).

Таким образом, мы получаем бесконечную систему дискретных уровней энергии, соответствующих всем положительным целым значениям квантового числа n. Каждому уровню принадлежит только одна собственная функция; число узлов (внутри потенциальной ямы) у n-й собственной функции равно n - 1.

Конечный скачок потенциала. Если потенциальная энергия имеет вид. показанный на рис. 6.2.2,б, то общее решение (6.2.20), по-прежнему справедливое при | x | < а , так как уравнение (6.2.19) в этой области не меняется, необходимо дополнить решением в области | x | > а. В этой области (вне потенциальной ямы) волновое уравнение имеет вид

и его общее решение при Е < U₀ (для связанного состояния) дается формулой

(6.2.21)

причем, в силу ограниченности волновой функции на бесконечности в облас-ти х > а нужно принять равной нулю константу D , а в области  x  < -а – кон-станту С.

Наложим теперь на решения (6.2.20) и (6.2.21) условия непрерывности волновой функции ψ и ее производной dψ/dx в граничных точках х = ±а:

,

,

Отсюда получаем

, , (6.2.22)

, , (6.2.23)

При А ≠ 0 и С ≠ D из уравнений (6.2.22) следует:

(6.2.24)

Аналогично при В = 0 и С = -D из уравнений (24) получим

(6.2.25)

Уравнения (6.2.24) и (6.2.25) нельзя удовлетворить одновременно, так как, исключив из них β мы получим tg²αа = -1, откуда в противоречии с (6.2.21) следует, что α – мнимое, а β – отрицательное число. Нельзя также требовать, чтобы все постоянные А., В, С и D обращались в нуль. Поэтому решения снова можно разделить на два класса. Для первого класса

A = 0 , C = D αtgαa = β ,

а для второго класса

B = 0 , C = -D αctgαa = β ,

Энергетический спектр электронов (разрешенные уровни энергии) находится путем численного иди графического решения уравнений (6.2.24) и (6.2.25). где α и β определяются выражениями (6.2.20) и (6.2.21).

Рассмотрим графический метод решения, позволяющий с полной ясностью выявить зависимость числа дискретных уровней от U₀ и а.

Положим ξ = αa, η = βа: тогда уравнение (6.2.25) примет вид ξ tgξ, = η, причем

.

Поскольку величины ξ и η могут принимать только положительные значения, уровни энергии определяются (лежащими в первом квадранте) точками пересечения кривой η = ξ·tgξ с окружностью заданного радиуса . На рис. 6.2.3 изображено необходимое построение для трех значений U₀ a². Двум меньшим значениям этого произведения п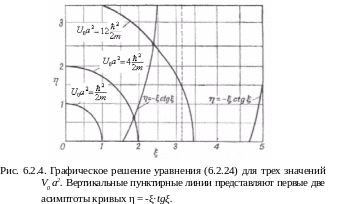 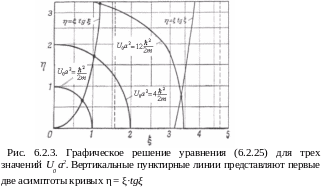ринадлежит по одному, а большему – два решения уравнения. (6.2.25).

На рис. 6.2.4 аналогичное построение проведено для уравнения (6.2.24), когда уровни энергии определяются пересечением тех же окружностей с кривой η = -ξ·tgξ (в первом квадранте). Для наименьшего значения U₀ a² решение отсутствует, а двум другим принадлежит по одному решению. Таким образом, всего для трех последовательно возрастающих значений U₀ a² имеется соответственно один, два и три уровня энергии.

Из рис. 6.2.3 и рис. 6.2.4 ясно, что при заданной массе частицы уровни энергии зависят от параметров потенциальной ямы через произведение U₀ a². Если значение U₀ a² лежит между нулем и , то имеется лишь один уровень энергии первого класса; в области имеется по одному уровню энергии каждого класса , т. е, всего два уровня. По мере возрастания U₀ a² уровни анергии последовательно появляются то для одного класса решений, то для другого. С помощью (6.2.20) нетрудно видеть, что если расположить собственные функции в порядке возрастания собственных значений, то у n-й собственной функции будет n-1 узел.