3.3. Линейные дефекты кристаллической решетки.

Дислокации образуются:

1. При росте кристаллов из расплава

2. При срастании слегка разориентированных дендритов

3. При захлопывании вакансий

4. Вследствие неоднородности химического состава

5. При пластической деформации

6. З а счет источника Франка-Рида.

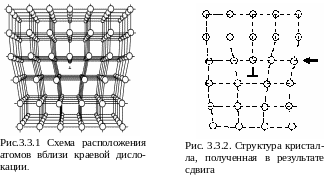
Важным видом дефектов являются – дислокации (рис. 3.3.1). Наиболее простой и наглядный способ введения дислокаций в кристалл – это сдвиг. Структура кристалла, полученная в результате сдвига, показана на рис. 3.3.2. В верхней части рисунка оказывается на одну вертикальную атомную плоскость больше, чем в нижней. Одна «лишняя» плоскость оказывается оборванной и не имеет продолжения внизу. Такую неполную плоскость называют экстраплоскостью. Край экстраплоскости является линейным дефектом и называется краевой дислокацией. Область кристалла непосредственно вокруг края экстраплоскости называют ядром дислокации.

Для оценки величины искажений кристаллической решетки вблизи дислокации Бюргерс предложил построить замкнутый контур вокруг участка кристалла, содержащего дислокацию, а затем построить такой же контур на участке кристалла с правильной решеткой.

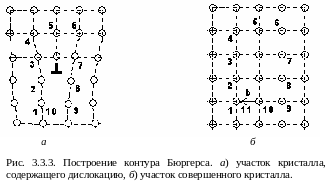Как видно из приведенного рисунка 3.3.3, для построения замкнутого контура вокруг участка, содержащего дислокацию, потребовалось 10 шагов. При построении аналогичного пути из 10 шагов в области совершенного кристалла контур не замыкается. Для замыкания контура требуется еще один шаг (b), в настоящее время называемый вектором Бюргерса. Построение контура Бюргерса в участке кристалла содержащего дислокацию можно начинать из произвольной точки и в любом направлении. Однако всегда в случае краевой дислокации вектор Бюргерса оказывается перпендикулярным линии краевой дислокации.

В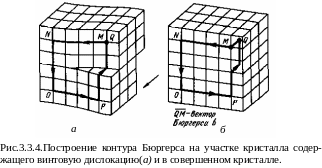 связи с этим у Бюргерса возник вопрос: нельзя ли представить дислокацию, вектор смещения которой параллелен линии дислокации? В 1939 году он предложил геометрический образ такой дислокации и назвал ее винтовой дислокацией.

Как видно из рис. 3.3.4,а , при круговом движении по плоскости перпендикулярной винтовой дислокации происходит смещение на следующую плоскость аналогичное движение по винтовой лестнице.

П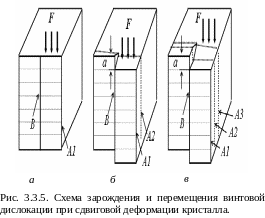 оэтому такой дефект называют винтовой дислокацией. Появляется винтовая дислокация при деформации кристалла по схеме, изображенной на рис. 3.3.5. Рассмотрим в случае простой кубической решетки плоскость типа {100}. Если на кристалл воздействовать силой ( рис. 3.3.5,а), то плоскость А1 в месте, отмеченном стрелочкой, может «разорваться» по линии В, после чего нижняя и верхняя половинки плоскости А1 соединятся со сдвигом на 1 период решетки (рис. 3.3.5,б). Если продолжать воздействие на кристалл, то следующая плоскость разорвется, после чего нижняя и верхняя половинки плоскости А2 соединятся со сдвигом (рис. 3.3.5,в), и так далее. Таким образом, в кристалле появится винтовая дислокация, которая при воздейст-вии на кристалл будет перемещаться вдоль плоскости скольжения за счет разрыва – соединения соседних половинок плоскостей. Заметим, что разрыв новой плоскости происходит как раз на линии дислокации, поскольку именно на ней искажения кристаллической решетки наибольшие (рис. 3.3.5).

У вектора Бюргерса есть ряд особенностей:

1. вектор Бюргерса нонвариантен, то есть не зависит от выбора контура обхода. Отсюда следует, что дислокация не может оборваться в кристалле;

2. энергия упругих искажений решетки пропорциональна квадрату модуля вектора Бюргерса;

3. при прохождении решеточной дислокации с вектором Бюргерса, равным периоду решетки, кристаллическая решетка не изменяется.

При приложении внешних напряжений дислокации смещаются и выходят на поверхность кристалла, и таким образом осуществляется пластическая деформация. Очевидно, что перемещение дислокаций вдоль плотноупакованных направлений и в плотноупакованных плоскостях осуществляется легче, чем в не плотноупакованных направлениях, вдоль которых расстояния между атомами больше. Следовательно, материалы с плотноупакованными кристаллическими решетками  металлы  обладают высокой пластичностью.

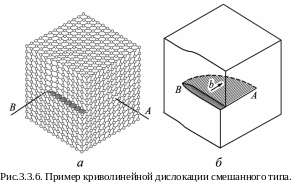
Дислокации смешанного типа. На рис. 3.3.6. приведен пример криво-линейной дислокации смешанного типа, соединяющей точки А и В. Видно, что в точке А расположение атомов отвечает краевой, а в точке В – винтовой дислокации. Такая дислокация может быть получена сдвиговой неоднород-ной деформацией.

Дислокации могут взаимодействовать. Дислокация создает поля деформаций, которые могут воздействовать на другие дислокации. Дислока-ции могут притягиваться или отталкиваться между собой.

Присутствие в кристаллической решетке дислокаций оказывает решающее влияние на механические свойства материалов. При полном отсутствии дислокаций прочность кристаллов должна была бы быть в сотни раз выше реальной. В обычных же материалах дислокации всегда присут-ствуют, поэтому их прочность существенно ниже теоретической. Подтверж-дением этого положения является создание нитевидных кристаллов, так называемых "усов". Усы из-за малого диаметра кристалла практически сво-бодны от дислокаций, и поэтому их прочность приближается к теорети-ческой.

Взаимодействие дислокаций и точечных дефектов. Дислокация, особенно краевая, создает сильно сжатые и сильно растянутые участки кристаллической решетки (рис. 3.3.7). В растянутые места энергетически выгоднее переместиться крупным атомам примеси замещения, а в сжатые - мелким атомам примеси замещения. Атомам внедрения, особенно крупным, также выгоднее перемещаться в область растянутой кристаллической решетки вблизи дислокации.

В растянутые места энергетически выгоднее переместиться крупным атомам примеси замещения, а в сжатые – мелким атомам примеси замещения. Атомам внедрения, особенно крупным, также выгоднее перемещаться в область растянутой кристаллической решетки вблизи дислокации. В таком случае вблизи дислокации образуется скопление примесей, называемое «шубой дислокации», которое уменьшает локальную деформацию вблизи дислокации и энергию дислокации. При пластической деформации сдвинуть такую дислокацию с места труднее, чем дислокацию без "шубы", поскольку в первом случае дислокация сместится на новое место, где ее энергия будет больше. Считают, что отдельные точечные дефекты и их скопления закрепляют дислокацию. В электронный микроскоп удается заметить появление крупных примесей вблизи дислокации. Рассматриваемый в теории прочности «зуб текучести» связывают с отрывом дислокации от шубы, для чего требуется дополнительное усилие.

Как уже отмечалось, дислокации появляются главным образом в результате пластической деформации кристаллов. Одним из источников дислокаций при пластической деформации считают источник Франка-Рида, схематически изображенный на рис. 3.3.8. Пусть дислокация 1 закреплена в точках А и В. Такими точками могут быть скопления атомов иного размера, область другой фазы и т.п. При приложении внешнего механического напряжения дислокация перемещается, последовательно занимая положения 2, 3, 4. Наконец в положении 5 левая и правая полупетли дислокации схлопываются, образуя дислокационную петлю 6 округлой формы. При наличии достаточного внешнего механического напряжения процесс повторится, , а далее процесс повторится и зародится следующая дислокация (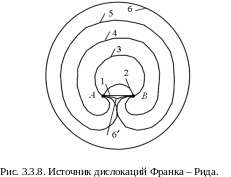 кривая 6′ примет сначала форму 1) и так далее.

Также замкнутые дислокации появляются при образовании дископо-добных скоплений вакансий (рис. 3.3.9) при охлаждении кристалла.

У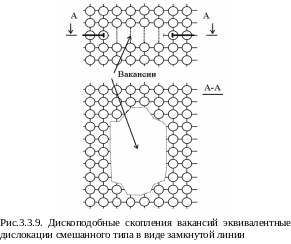 частки кристалла с растянутой кристаллической решеткой вблизи дислокации являются своеобразными каналами облегченной диффузии. Известно, что диффузия в сильно деформированных материалах, в которых плотность дислокаций больше, происходит быстрее, чем в недеформиро-ванных.

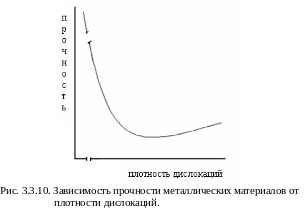
При повышении плотности дислокаций в обычных материалах их прочность возрастает. Это связано с тем, что в ядре дислокации кристал-лическая решетка искажена, следовательно, дислокации окружены полями упругих напряжений. При увеличении плотности дислокаций поля упругих напряжений перекрываются, дислокации взаимодействуют друг с другом, и перемещение дислокаций затрудняется. Хотя прочность материалов с повы-шенной плотностью дислокаций всего лишь в полтора – два раза выше прочности материалов с обычной плотностью дислокаций, такое повышение прочности имеет большое практическое значение. Повышение плотности дислокаций легко провести путем холодной пластической деформации. Повышение прочности металлов в ходе холодной пластической деформации называют наклепом, или нагартовкой.

Зависимость прочности металлических материалов от плотности дислокаций показана на рис. 3.3.10.

Наличие в материале дислокаций резко повышает скорость диффузии. Это связано с тем, что дислокации могут являться источниками и стоками вакансий. При испускании вакансий дислокации переползают на плоскость лежащую выше, а при поглощении вакансий дислокации переползают на плоскость, лежащую ниже исходной плоскости. Таким образом, наличие дислокаций повышает локальную концентрацию вакансий, а следовательно, ускоряет диффузию. Этим пользуются опытные мастера, прежде чем затачивать жало паяльника они отбивают его. Тогда при облуживании жала припоем, олово, входящее в состав припоя, диффундирует в медное жало, и на поверхности жала образуется тонкий слой сплава меди с оловом – бронзы. Коррозионная стойкость материала повышается, и жало паяльника служит дольше.

Дислокации взаимодействуют с атомами растворенных примесей или легирующих элементов. Как отмечалось выше, вблизи чужеродного атома кристаллическая решетка искажена - растянута или сжата. В ядре дислокации кристаллическая решетка также искажена: под экстраплоскостью кристал-лическая решетка растянута, а над экстраплоскостью сжата. Поэтому чужеродные атомы притягиваются к дислокациям, образуя скопления, которые называют атмосферы Котрелла. При движении дислокаций вместе с ними перемещаются и атмосферы Котрелла, что приводит к затруднению движения дислокаций или к повышению прочности металлических материалов. Поэтому сплавы прочнее чистых металлов.

Искажение кристаллической решетки за счет присутствия дислокаций повышает удельное электрическое сопротивление металлических материалов и снижает удельное электрическое сопротивление неметаллических материалов. Природа влияния дислокаций на электрические свойства материалов аналогична природе влияния точечных дефектов.

Д ислокации и рост кристаллов. Винтовые дислокации облегчают рост кристаллов (как из расплавов, так растворов и паров), поскольку ступенька на поверхности кристалла (рис. 3.3.11), связанная с винтовой дислокацией, облегчает осаждение атомов на поверхность кристаллов в местах обозна-ченных на рис. 3.3.11 буквой А. Атомы прикрепляются под ступенькой большим числом связей, чем на гладкой поверхности кристаллов. На поверхности достаточно совершенных кристаллов часто наблюдают следы подобных ступенек.