12.3.8. Эллипсометрия.

Эллипсометрия представляет собой метод неразрушающего Конт-роля и измерения параметров поверхности вещества по поляризационным характеристикам отраженного и проходящего излучения.

В основе метода эллипсометрии лежат измерения характеристик полностью поляризованной световой волны при отражении ее от исследуе-мой поверхности. Для такой волны характерна полная поляризация (когерентность) колебаний взаимно ортогональных компонент электри-ческого вектора световой волны Е. Другими словами, имеет место постоянст-во амплитуды, разности фаз, а сами компоненты изменяются во времени по гармоническому закону. На рис. 12.3.36 приведены схематические изобра-жения электрического вектора при сложении двух волн различной поляри-зации.

Наиболее информативным является случай эллиптически поляризо-ванной световой волны.

Для описания поляризованного света используются соотношения

, (12.3.20)

,

где Е_y и E_z – проекции вектора Е плоской монохроматической волны, распро-страняющейся по оси x, на ортогональные координаты y, z;

 – полная фаза волны; Т – период электрических колебаний; t – текущее время; δ – начальный постоянный фазовый сдвиг.

При сложении двух типов колебаний для ряда значений δ получаются различные модификации эллипса.

На рис. 12.3.37 показано поведение электрического вектора Е плоской монохроматической волны в соответствии с соотношениями

,

, (12.3.21)

,

.

Таким образом, конец вектора Е описывает в пространстве эллиптическую спираль, параметры которой зависят от E_0y и E_0z , a также от сдвига фаз δ.

В процессе измерений поляризованный свет направляют на исследуемую поверхность. Отраженный свет будет нести информацию о состоянии поверхности. Анализ отраженного света производится с помощью системы оптических и фотоэлементов.

На рис. 12.3.38 приведена схема отражения плоской монохроматичес-кой волны от однородной среды с плоскопараллельными слоями.

Электрическое поле Е волны представимо в виде суммы компонет

, (12.3.22)

где е_р и е_s  – единичные векторы, лежащий в плоскости падения и перпенди-кулярный плоскости падения соответственно. Оба этих вектора перпендику-лярны вектору k.

В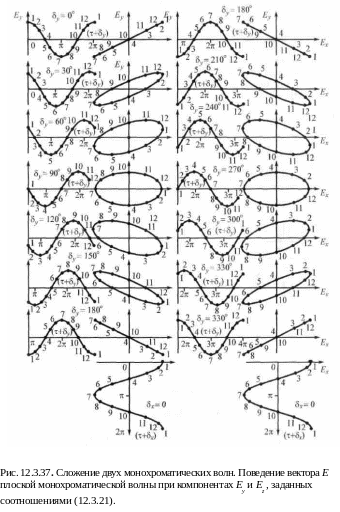 прямоугольной системе координат электрическое поле плавающей волны запишется в виде

, (12.3.23)

,

а отраженной волны соответственно

, (12.3.24)

,

г де , , ,  –  комплексные амплитуды, k₀ и  – волновые векто-ры падающей и отраженной волн. В результате отражения вектор плоской волны будет описывать эллипс представленный на рис. 12.3.39.

Угловые характеристики эллипса определяются отношением модулей и разностью фаз р- и s-составляющих комплексной амплитуды.

Коэффициенты отражения R_р и R_s определяются формулами Френеля для отражения света и являются функциями оптических постоянных отража-ющей системы, толщины плоскопараллельных слоев, угла падения света ψ и длины волны излучения. В общем случае их можно записать в виде

, (12.3.25)

Относительный коэффициент отражения ρ = R_р / R_s описывает измене-ние состояния поляризации в результате отражения. Значение

(12.3.26)

является комплексной величиной. Тогда

,

.

Уравнение (12.3.26) называется основным уравнением эллипсометрии.

Углы Δ и ψ характеризуют относительный коэффициент отражения. Вычисляя R_р и R_s для конкретной отражающей поверхности с помощью уравнения (12.3.26), устанавливают связь поляризационных углов с оптическими постоянными и толщинами слоев исследуемой поверхности, а также углом падения φ и длиной волны λ излучения.

Из уравнения (12.3.23) и (12.3.24) имеем

или

,

а также

,

Без вывода, отсылая к справочной литературе запишем:

, (12.3.27)

Тогда находим связь поляризационных углов отражающей системы ψ и Δ с углами ψ₀, Δ₀ и ψ₁ и Δ₁

.

Комплексное основное уравнение эллипсометрии (12.3.26) удобно записать в виде двух уравнений

, (12.3.28)

.

где φ_l = Re (R_p/R_s), φ₁= Im (R_p/R_s).

Таким образом, измеряя углы ψ и Δ и решая совместно уравнения (12.3.28), можно определить два любых неизвестных параметра исследуемой системы. При определенных условиях можно вычислить и более двух неизвестных параметров исследуемой поверхности, поэтому для корректного исследования поверхности необходимо решить три основные задачи:

1. Вычислить поляризационные углы ψ и Δ;

2. Экспериментально определить эти углы;

3. Сравнить вычисленные значения с экспериментально полученными и установить модель, адекватную исследуемой поверхности.

После установления адекватной модели метод эллипсометрии можно использовать для контроля параметров поверхности, исследования измене-ния этих параметров под влиянием внешних или внутренних воздействий.

Методы исследования поверхности можно разделить на 2 группы: нулевые и ненулевые методы. Рассмотрим наиболее распространенные нуле-вые методы.

Н улевые методы основаны на установлении взаимосвязи между поляризационными углами ψ и Δ и теми положениями элементов эллипсо-метров, которым отвечает минимум интенсивности, или гашение светового пучка на выходе. Принципиальная схема эллипсометра нулевого метода представлена на рис. 12.3.40. Излучение от лазерного источника Л проходит через поляризатор П, после которого пучок становится линейно-поляризованным. После отражения луч света проходит через компенсатор К, который вносит дополнительную разность фаз. Анализатор А позволяет выявить характер поляризации после отражения от исследуемого объекта.

В основе нулевых методов лежат соотношения, связывающие по-ляризующие углы ψ и Δ с углами ψ ₀ и Δ₀ отраженной и падающей волны соответственно,

, (12.3.29)

.

В нулевом методе измерения углов ψ₀, Δ₀ и ψ_{1 ,} Δ₁ задача измерения решается реализацией гашения света на выходе анализатора.

На схеме (рис. 12.3.40,а) падающая на поверхность волна всегда по-ляризована линейно, другими словами, разность фаз Δ₀ фиксирована: Δ₀ = 0 и Δ₁ = π.

На схеме (рис. 12.3.40,б) с помощью анализатора добиваются линейной поляризации отраженного света. Другими словами, Δ₁ всегда фиксированна: Δ₁ = 0 или Δ₁ = π.

В нулевых методах возможно использование циркулярно поляризо-ванного света.

Методы отражательной эллипсометрии применяются для иссле-дования поверхностей веществ с большим поглощением. Это прежде всего, металлы и полупроводники. Особое значение эллипсометрические методы приобретают при исследовании эпитаксиальных слоев, слоев окислов, адсорбированных и адгезионных слоев.

Разработаны методы неразрушающего контроля роста слоев и пленок кристалла.