
- •Числовое моделирование гидрации портландцемента
- •1.Введение
- •2.3. Влияние межчастичного взаимодействия
- •Vpore – полный объем капиллярных пор;
- •2.5. Концепция полиминеральности (сложного состава/структуры).
- •2.8. Структурные изменения гидратов
- •3. Определение параметров модели
- •4. Оценка параметров модели
- •5. Выводы/Заключение
Числовое моделирование гидрации портландцемента
И. Марияма
Университет Нагои, Нагоя, Япония;
1.Введение
За последние несколько десятилетий было сделано несколько исследований в области моделирования гидратации цемента для того, что бы оценить поведение зависимости схватывания от времени материалов на основе цемента [1-3]. В недавних исследованиях, для моделирования сложных процессов гидратации, и особенно для исследований, направленных на микромеханику процессов гидратации, использовались возможности современных компьютеров [4-5]. Пытаясь описать, в общем, что же делает сложным процесс моделирования гидратации цемента и почему необходимо для понимания использовать компьютер, были выявлены два важных направления.
Первое, это физический аспект. Свойства цементной матрицы, состоящей из частиц цемента и воды, определяются и водоцементным отношением, и распределением частиц по размеру [7]. В процессе гидратации, частицы цемента взаимодействуют с водой с образованием гидратов и формируют структуру цементной матрицы. Таким образом, физический аспект оказывает влияние на гидратацию цемента посредством диффузии ионов [3-5]. Вторая важная переменная – цемент это полиминеральный материал, его компоненты взаимодействуют между собой. А так же, большое влияние на гидратацию цемента оказывает температура с химической точки зрения [2,6]. Эти две переменные имеют взаимосвязанные отношения по причине диффузии ионов и воды и формирования структуры. Эти отношения нельзя выразить простым уравнением. Однако использование возможностей компьютера и концепцию дискретно-событийного моделирования делает возможным описание процесса гидратации цемента. В этом исследовании, основанном на модели Томосавы, модели для цементной матрицы названной CCBM («вычислительная модель для материалов на основе цемента»), предложена модель для потенциального описания свойств бетона на основании результатов эксперимента.
2. Модель гидратации
2.1. Предпосылки
Предложенная модель гидратации основана
на фундаментальной кинетической модели
для портландцемента, разработанной
Томосавой [8]. Модель Томосавы, которая
в оригинале дана в литературе [2], выражена
одной формулой (Формула (1)), состоящей
из четырёх коэффициентов, которые
определяют соотношение процессов
формирования к процессам разрушения
первичного непроницаемого слоя, процесс
активации химической р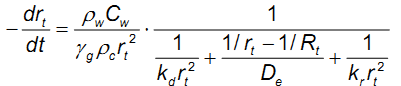 еакции
и последующее ослабление диффузии
контролируемого процесса:
еакции
и последующее ослабление диффузии
контролируемого процесса:
Формула (1)
где rt – первоначальный радиус негидратированной частицы цемента, мм
Rt – полный радиус частицы цемента, с учетом толщины слоя геля, мм
De – коэффициент эффективной диффузии воды через цементный гель, мм2/ч
kr - коэффициент скорости реакции на единицу площади реакционного фронта, мм/ч
kd – коэффициент устойчивости защитного слоя в индукционный период, мм/ч
γg – стехиометрическое отношение массы воды к массе цемента
ρс – плотность цемента,
ρw – плотность воды
Сw – пространственная плотность воды в цементной матрице
Этот первоначальный подход показывает высокий потенциал моделирования процесса гидратации. Однако, четыре коэффициента, просто подогнаны под модель Томосавы и они не передают никакой информации о свойствах цемента. Это может быть логически объяснено тем, что целью этой модели является процесс гидратации частицы цемента, а не моделирование формирования цементной матрицы.
Допущения
Для модели Томосавы были приняты следующие первоначальные допущения и дополнительные изменения:
Реакция гидратации начинается в момент контакта зерна цемента с водой.
В процессе гидратации образуется гидрат, который прилипает в поыерхности зерна цементе. Гидрат будет образовываться путем нуклеации, до тех пор пока межзерновые контакты не увеличатся. Непрогидратировавший цемент сохраняет сферическую форму. Новый гидрат образуется на поверхности без ограничения роста межзерновых контактов. Если поверхность одной частицы сталкивается/перекрывается с поверхностью другой, то гидрат перестаёт образовываться/больше не образуется.
Гидрат имеет столько же v, сколько и первоначальная частица цемента в объёме.
Жидкая фаза, которая, как предполагается является водой диффузирует через слой гидратных новообразований и достигает поверхности частицы цемента и вступает в химическую реакцию с цементом. Этот процесс продолжается вместе с реакцией гидратации. Часть образовавшегося на поверхности гидрата движется сквозь слой гидратных новообразований. Отсюда следует, что в гидратном слое имеет место эквимолярная диффузия воды и продуктов гидратации.
Коэффициент диффузии в гидратном слое для воды одинаков для входящих и выходящих продуктов. На коэффициент диффузии влияют извилистость гелевых пор, так же как и радиус гелевых пор в гидрате. Это феномен можно выразить функцией степени гидратации.
Распределение частиц цемента по размерам может быть выражено функцией Розина Раммлера. Частицы, имеющие приблизительно одинаковый диаметр, имеют одинаковую скорость гидратации.
Индукционный период в начальном процессе гидратации является периодом, в который скорость гидратации возрастает с увеличением степени гидратации в каждой частичке (пленкообразование). За ним следует период, в котором скорость гидратации уменьшается с увеличением толщины внутренних продуктов/плёнок/новообразований.
2.2. Распределение/различность частиц по размеру
Распределение частиц цемента по размеру играет большую роль в процессе гидратации цемента [9]. При определении степени гидратации как соотношения объема прореагировавшего цемента к первоначальному объему, гидратация частиц различных размеров идет с различной скоротью, когда как предположительно скорость реакции является постоянной для всех частиц цемента. Также, суммарная степень гидратации всего цементного теста должна является результатом различных степеней гидратации каждой частицы. В предложенной модели предполагается, что распределение частиц цемента может быть выражено через формулу Розина Рамлера (Формула (2)).
![]() Формула (2)
Формула (2)
Где V(r0) – массовое соотношение/массовая доля частиц цемента с радиусом r < r0 , г/г; b и n - коэффициенты распределения
