
- •1.Основные понятия
- •2. Компьютерное исследование точности
- •3.Исследование датчиков псевдослучайных чисел
- •3.1 Генерация псевдослучайных чисел
- •3.1.1 Генерация равномерных чисел
- •3.1.2 Генерация случайных чисел,
- •3.2 Тестирование датчиков
- •3.2.1.Проверка на соответствие заданному закону
- •3.2.2. Проверка независимости и некоррелированности
- •3.3. Наиболее часто встречающиеся законы распределения
- •3.4. Контрольные вопросы
- •4. Оценка параметров распределения
- •4.1. Вычисление точечных оценок
- •4.2. Вычисление интервальных оценок
- •4.2.1.Интервальная оценка дисперсии
- •4.2.2.Интервальная оценка математического ожидания
- •4.3. Точность оценивания параметров
- •4.4.Контрольные вопросы
- •5.1. Проверка гипотезы о математическом ожидании
- •5.2. Проверка гипотезы о дисперсии нормально распределенной
- •5.3. Проверка гипотезы о параметре экспоненциального
- •5.4. Точность проверки
- •5.5. Контрольные вопросы
- •6. Проверка статистических гипотез по критериям значимости (согласия)
- •6.1. Критерий значимости (согласия)
- •6.2. Проверка гипотез о параметрах нормально распределенной случайной величины
- •6.4. Точность проверки гипотез по критериям значимости
- •6.5. Контрольные вопросы
- •7.1.2.Проверка гипотезы по критерию Вилкоксона
- •7.2. Проверка гипотезы о наличии статистической независимости
- •7.2.1 Коэффициент ранговой корреляции Спирмена
- •7.2.2. Коэффициент ранговой корреляции Кендалла
- •7.3. Исследование точности ранговых критериев
- •7.4. Контрольные вопросы
3.4. Контрольные вопросы
1. Что такое «псевдослучайные» числа?
2. Как проверить последовательность чисел на независимость?
3. Каким образом можно генерировать псевдослучайные последовательности в ЭВМ?
4. Для генерации каких законов распределения можно использовать метод обращения функции распределения?
5. Как реализовать на ЭВМ генерацию распределения произвольного вида?
6. Как реализовать на ЭВМ метод моделирования распределения?
7. Предложите несколько способов генерации нормально распределенных последовательностей и сравните их по быстродействию.
8. Дайте сравнительную характеристику и оценку методов генерации, изложенных в разд. 3.1.
9. Каковы области применения критерия согласия «λ – Колмогорова» и « – Пирсона»?
4. Оценка параметров распределения
Одна из наиболее распространенных задач математической статистике заключается в оценивании по выборке ограниченного объема параметров распределения случайной величины (математического ожидания, дисперсии и т.д.). Для этого применяются точечные и интервальные оценки.
Точечной называют оценку, которая
определяется одним числом
![]() где
где
![]() – набор значений случайной величины
X, полученных в результате
n опытов , т.е. выборка
объемом n. Обычно
предполагается, что опыты произведены
в одинаковых условиях и независимы.
– набор значений случайной величины
X, полученных в результате
n опытов , т.е. выборка
объемом n. Обычно
предполагается, что опыты произведены
в одинаковых условиях и независимы.
Интервальной называют оценку, которая
определяется несколькими числами,
например, концами интервала
![]() с заданной вероятностью γ, покрывающего
оцениваемы параметр.
с заданной вероятностью γ, покрывающего
оцениваемы параметр.
Числа
![]() и
и
![]() называют доверительными границами,
случайный интервал
называют доверительными границами,
случайный интервал
![]() – доверительным интервалом для параметра
a, число γ – доверительной
вероятностью.
– доверительным интервалом для параметра
a, число γ – доверительной
вероятностью.
4.1. Вычисление точечных оценок
Оценки должны обладать тремя свойствами: несмещенностью, состоятельностью и эффективностью.
Состоятельность означает, что с
увеличением объема выборки n
оценка
![]() сходится по вероятности к оцениваемому
параметру a:
сходится по вероятности к оцениваемому
параметру a:
![]() (4.1)
(4.1)
Несмещенной называют оценку, математическое ожидание которой равно оцениваемому параметру:
![]() (4.2)
(4.2)
Эффективность означает, что оценка обладает наименьшей дисперсией. Для характеристики эффективности оценок математического ожидания и дисперсии используют неравенство, дающее нижнюю границу дисперсии оценки:
 (4.3)
(4.3)
Использование неравенства (4.3) требует знания закона распределения измеряемой величины X – f(x,a).
Наиболее распространенным методом оценки параметров распределения случайной величины является метод статистических моментов, согласно которому в качестве оценки параметра принимается значение соответствующего статистического момента.
Статистический момент порядка k имеют вид
начальный
 (4.4)
(4.4)
центральный
 (4.5)
(4.5)
Статистические моменты, соответствующие наиболее употребительным параметрам распределения, выражаются формулами:
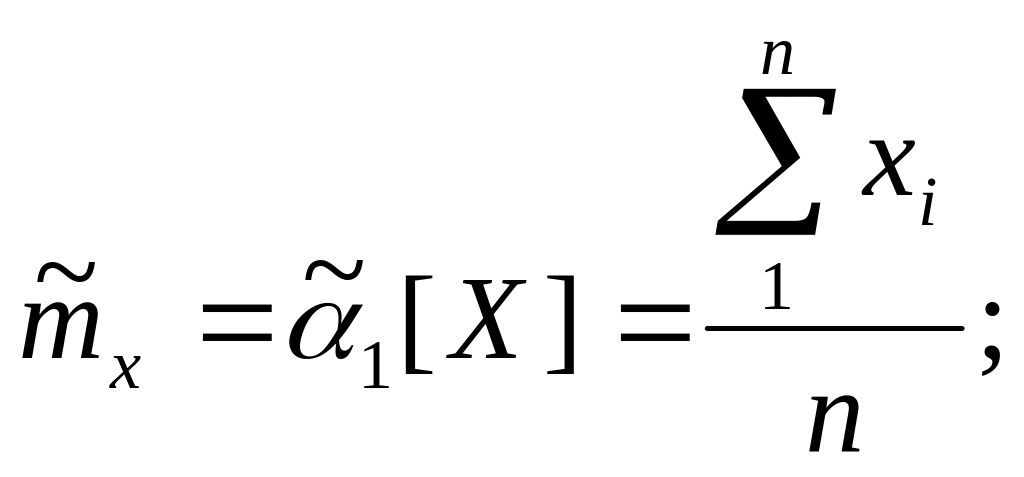 (4.6)
(4.6)
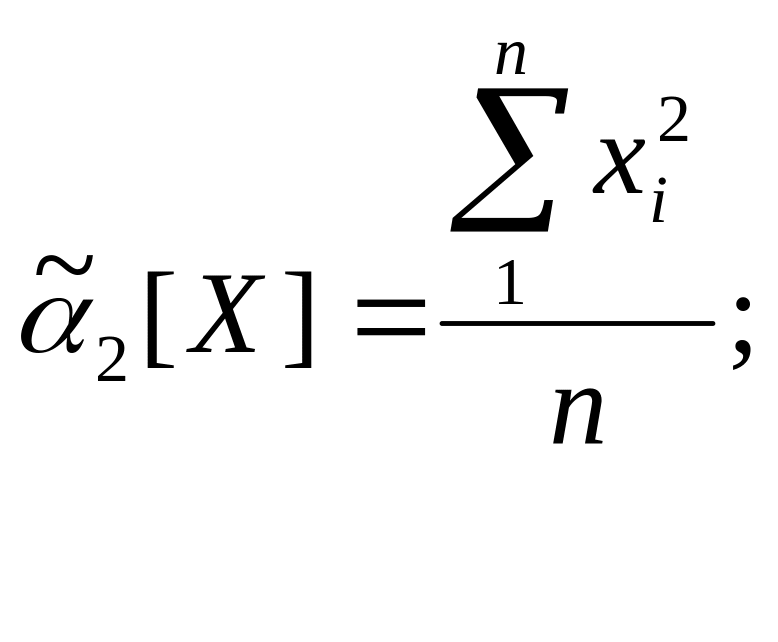 (4.7)
(4.7)
 (4.8)
(4.8)
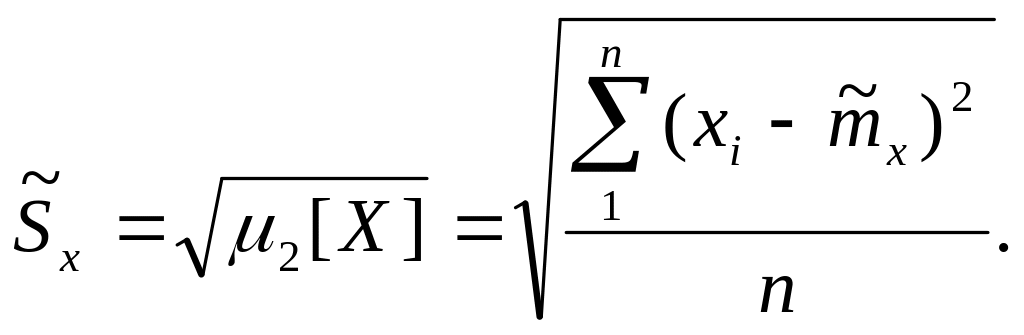 (4.9)
(4.9)
Статистики (4.6) и (4.7) отвечают перечисленным
требованием и могут использоваться в
качестве оценок m x
и α 2[X], а оценки
![]() и
и
![]() не
удовлетворяют требованию несмещенности.
Можно показать, что
не
удовлетворяют требованию несмещенности.
Можно показать, что
![]() (4.10)
(4.10)
т.е. оценка дисперсии по формуле (4.8) будет смещенной, причем величина смещения тем заметнее, чем меньше объем выборки n. Для устранения смещения оценки дисперсии и среднего квадратического отклонения (с.к.о.) вычисляют по формулам
 (4.11)
(4.11)
 (4.12)
(4.12)
Оценки дисперсии и с.к.о., вычисляемые в соответствии с (4.11) и (4.12), являются несмещенными.
Следует заметить, что если математическое
ожидание известно, то, подставляя его
в (4.8) и (4.9) вместо
![]() ,
получим несмещенные оценки Dx
и σx.
,
получим несмещенные оценки Dx
и σx.
