6.2. Проверка гипотез о параметрах нормально распределенной случайной величины

6.2.1. Проверка гипотезы о значении математического ожидания при известной дисперсии

В качестве критерия значимости принимается нормированная величина:

, (6.1)

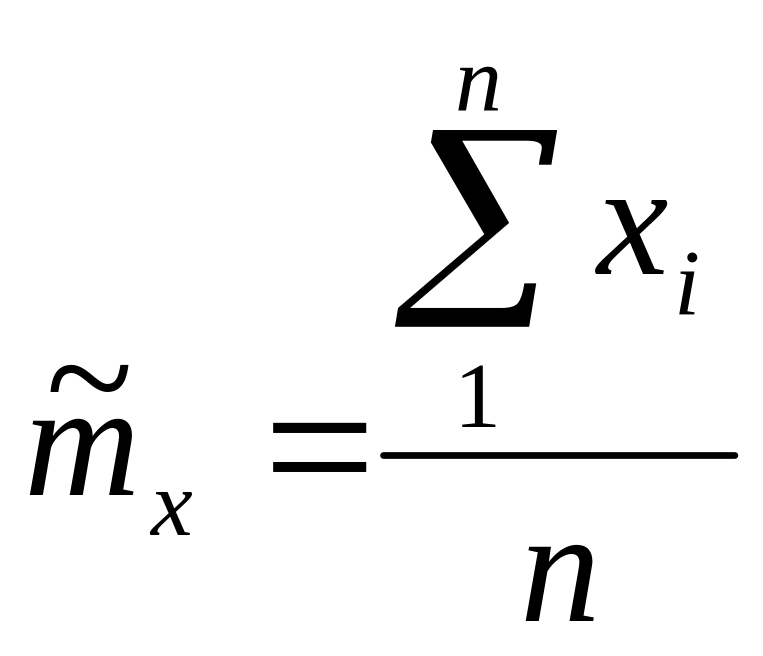
где - оценка математического ожидания; - гипотетическое значение математического ожидания; - известная дисперсия случайной величины Х; n – число наблюдений.

При нормальном распределении Х оценка математического ожидания в форме среднего арифметического подчинена нормальному распределению с параметрами и . Если гипотеза верна и , то критерий значимости следует нормированному нормальному распределению:

-∞<ξ<∞.

Задаваясь уровнем значимости q, находим по таблицам интеграла вероятности границы областей и R :

Гипотеза принимается, если вычисленные в соответствии с (6.1) значения критерия значимости лежат между и и отбрасывается в противном случае:

( < < ) – гипотеза принимаемости;

( < или > ) – гипотеза отбрасываемости.

При этом вероятность совершить ошибку первого рода равна q.

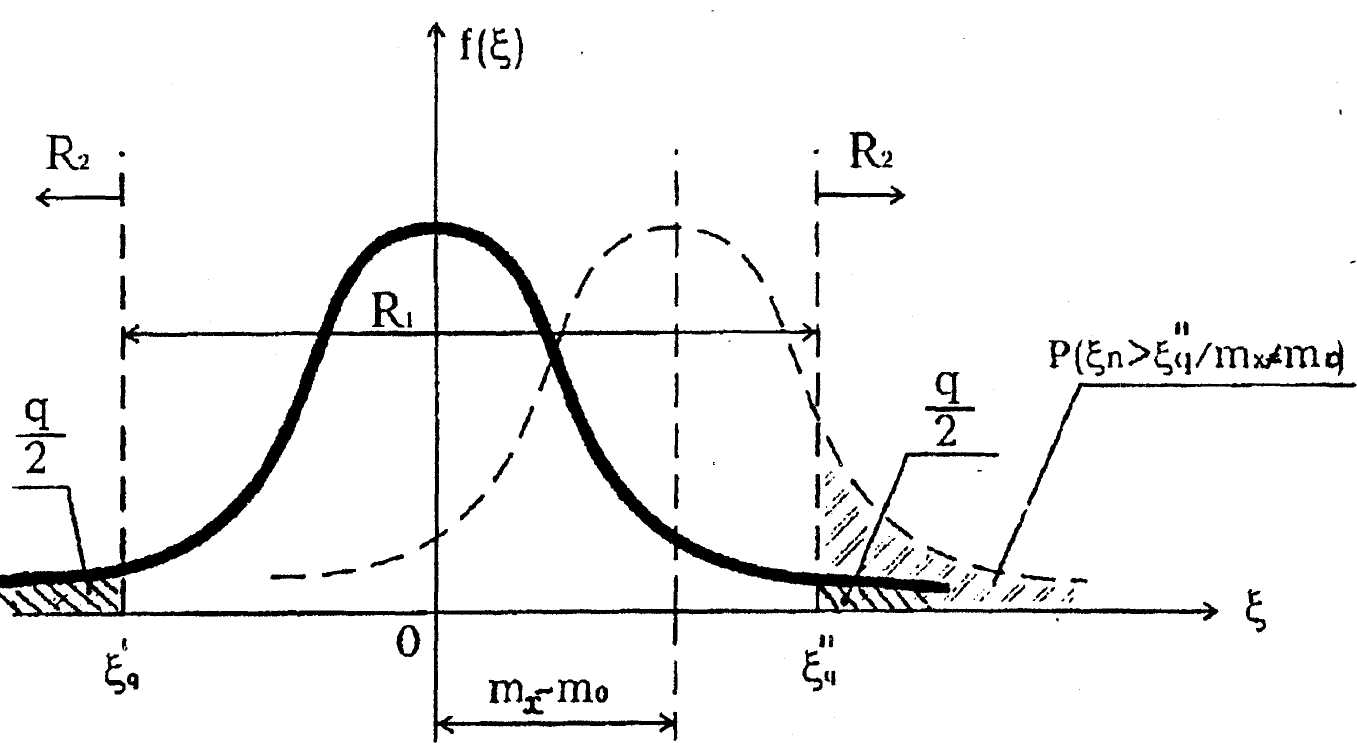
Рис. 3 иллюстрирует применение этого критерия.

Если гипотеза неверна , то распределение ξ по-прежнему остается нормальным с единичной дисперсией, однако его математическое ожидание уже равно На рис.3 пунктиром показано такое распределение. Из рис.3 видно, что в этом случае вероятность того, что критерий значимости ξ превзойдет , достаточно велика, что подтверждает обоснованность данного метода проверки гипотезы.

П р и м е ч а н и е. Если Х не является нормально распределенной величиной , но дисперсия ее известна, то при больших объемах выборки для проверки гипотезы о математическом ожидании можно применить эту же процедуру. Основанием этому служит то, что оценка , имеющая форму суммы независимых случайных величин, при больших n, в соответствии с центральной предельной теоремой, имеет распределение, достаточно близкое к нормальному, с параметрами и .

6.2.2. Проверка гипотезы о значении математического ожидания при неизвестной дисперсии

В этом случае в качестве критерия значимости удобно принять величину:

, (6.2)

где - смещенная оценка с.к.о.

Известно [2, 9], что случайная величина t подчинена распределению Стьюдента с (n - 1) степенями свободы. По таблицам распределения Стьюдента находим границы и из соотношения

Если экспериментально найдены критерий значимости отвечает неравенству , гипотеза принимается, в противном случае гипотеза отвергается.

6.2.3. Проверка гипотезы о значении дисперсии

В этом случае в качестве критерия значимости удобно принять отношение:

(6.3)

где - гипотетическое значение дисперсии.

Известно [2, 9], что отношение (6.3) подчинено - распределению с (n - 1) степенями свободы. Так как - неотрицательная случайная величина, то критерий значимости имеет односторонний характер (т.е. расхождения между гипотетическими и экспериментальными характеристиками могут быть только одного знака).

Значение , разделяющее область значений критерия на допустимую и критическую, по таблицам - распределения, находится из соотношения:

В случае, если , гипотеза принимается, если же - гипотеза отвергается.

П р и м е ч а н и е. Критерии значимости типа рассмотренных в разд. 6.2.1. и 6.2.2. называют двухсторонними, а типа из разд. 6.2.3. – односторонними критериями.

6.3.1. Проверка гипотезы о функции распределения непрерывной случайной величины по критерию согласия λ-Колмагорова

Критерий согласия λ-Колмагорова применяется для проверки гипотез о функции распределения непрерывных случайных величин, когда гипотетическое распределение полностью определено. Последнее означает, что ни одна из характеристик гипотетического распределения не основывается на выборочных данных.

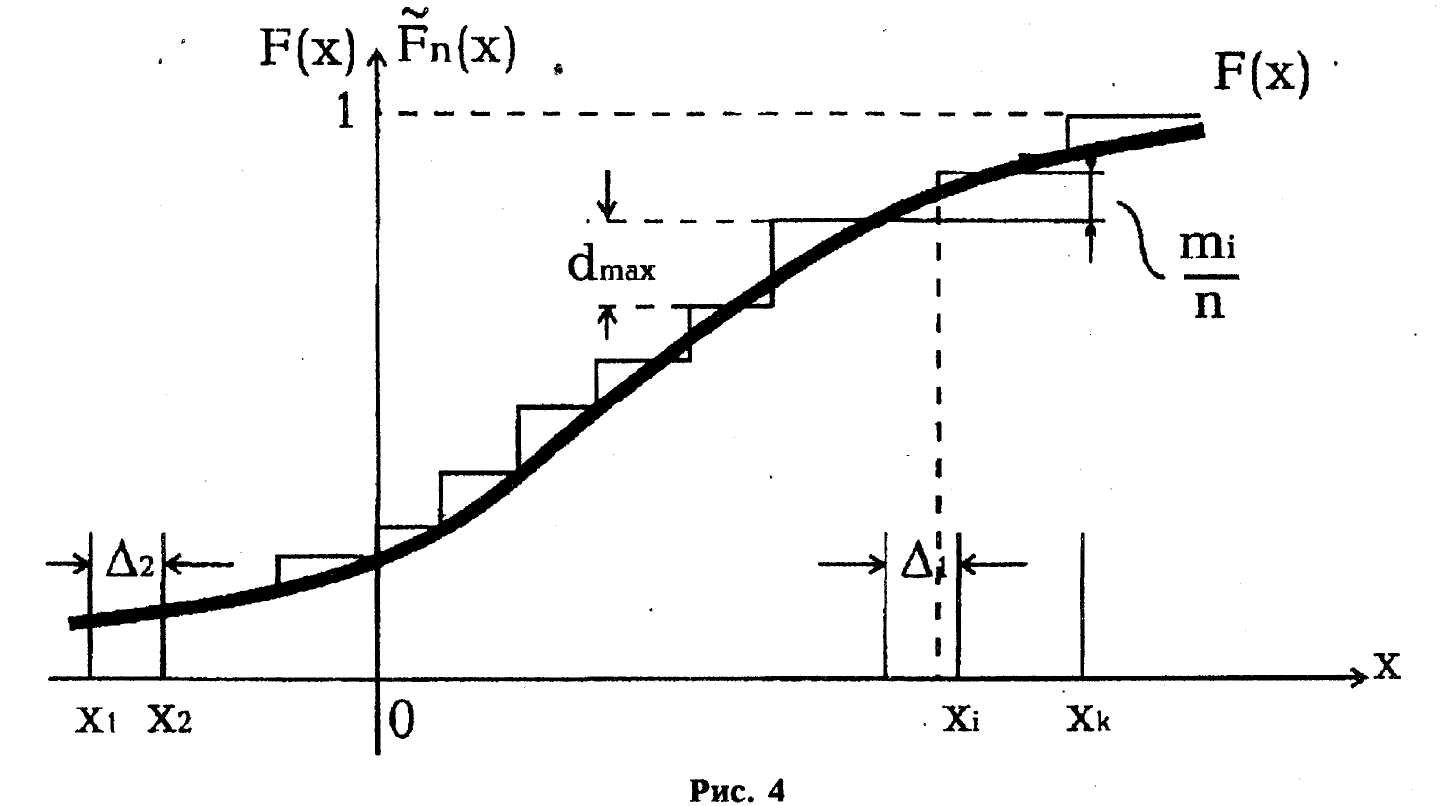
Пусть - эмпирическая функция распределения, построенная по выборке объема n (рис. 4, где - число наблюдений случайной величины в интервале); - гипотетическая функция распределения; можно рассматривать как состоятельную оценку функции распределения случайной величины Х.

Критерий согласия λ-Колмагорова основан на теореме Колмогорова, согласно которой

, (6.4)

где ; истинная функция распределения Х.

Из (6.4) видно, что представляет функцию распределения случайной величины . Это распределение табулировано.

Следует отметить, что распределение Колмагорова носит предельный характер и случайную величину можно считать подчиненной ему лишь при достаточно больших объемах выборки – n.

Пусть - максимальное расхождение между эмпирическим и гипотетическим распределениями:

. Отождествляя и и полагая, что гипотеза о распределении Ч верна, можем утверждать, что, если объем выборки достаточно велик, случайная величина подчинена распределению (6.4) Колмогорова. Величина λ и используется в качестве меры близости эмпирического и теоретического распределений. Так как λ неотрицательна, критерий согласия односторонний. По таблицам распределения Колмогорова находим для заданного уровня значимости q границу из соотношения .

Затем из сопоставления эмпирического и гипотетического распределений (рис. 4) находим и вычисляем . Если , гипотеза принимается. В противном случае гипотезу следует отвергнуть, так как слишком большое и соответственно маловероятное говорит о том, что, скорее всего, гипотеза о распределении Х неверна и поэтому применение распределения (6.4) некорректно, и граница получена ошибочно.

6.3.2. Проверка гипотезы о распределении случайной величины по критерию - Пирсона

ю и критическую, по таблицам ерсииизкое крахами распределения000000000000000

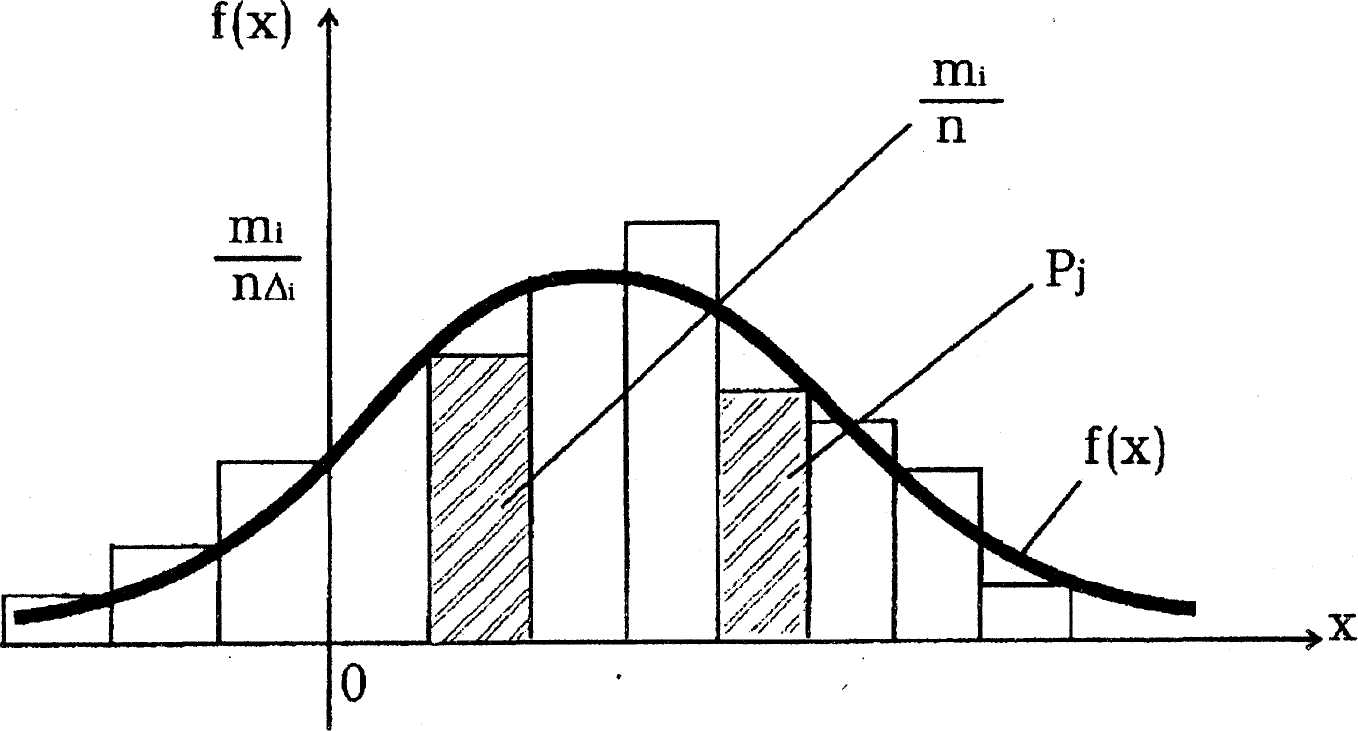
Метод проверки гипотез о распределении по критерию согласия λ-Колмагорова ограничен тем, что, как указывалось, применим лишь к непрерывным случайным величинам и полностью определенным гипотетическим распределениям. От этих ограничений свободен метод проверки по критерию согласия - Пирсона. В основу этого метода положена оценка близости гипотетической плотности распределения (для непрерывных Х) или ряда распределений (для дискретных Х) и эмпирического аналога этих характеристик, представленного гистограммой (рис. 5) или полигоном. Критерий согласия - Пирсона имеет вид:

, (6.5)

где - число наблюдений случайной величины Х в интервале ; - вероятность появления случайной величины Х в интервале , вычисленная в соответствии с гипотетическим распределением; k – число интервалов на которые разбита область возможных значений Х (или число возможных значений для дискретных Х).

В выражении (6.5) произведение имеет смысл математического ожидания числа наблюдений Х в интервале . Таким образом, критерий - Пирсона основан на сравнении эмпирически полученных чисел наблюдений случайной величины в интервалах с их математическим ожиданием, вычисляемым в предположении , что гипотеза верна. Форма критерия (6.5), а также нормирование этого критерия вероятностями обусловлено тем, что, как доказывается в теореме Пирсона, при увеличении объема выборки n распределение случайной величины, определяемой в соответствии с (6.5), стремится к - распределению. Число степеней свободы r этого распределения определяется как число разрядов k минус число связей s, наложенных на компоненты суммы (6.5): r=k-s.

Так, если гипотетическое распределение определено полностью, без использования выборочных данных, то на статистику (6.5) наложено единственное ограничение . Следовательно, s=1, r=k-1 и критерий согласия -Пирсона подчинен -распределению с (k-1) степенями свободы.

Если, например, математическое ожидание гипотетического распределения получено из выборки, т.е. принято равным его оценке , то на компоненты (6.5) наложена еще одна связь:

.

В этом случае s=2 и критерий -Пирсона имеет -распределение с (k-2) степенями свободы.

Если из выборки задавать не только математическое ожидание, но и дисперсию, то на компоненты (6.5) наложится еще одна связь:

и критерий (6.5) будет подчинен -распределению с (k-3) степенями свободы.

В соответствии с изложенным, проверка гипотезы о распределению по критерию -Пирсона сводится к следующему:

область возможных значений Х разбивается на k разрядов, при этом стремятся проводить разбиения так, чтобы все разряды были представительны, т.е. содержали бы несколько наблюдений;

формируется вариационный ряд;

в соответствии с гипотезой определяется число s связей, наложенных на сумму (6.5), и вычисляется число степеней свободы -распределения;

по таблице распределения для заданного уровня значимости q находится граница критической области из соотношения

;

по формуле (6.5) вычисляется эмпирическое значение критерия согласия ;

если вычисленное значение меньше , то гипотеза принимается, в противном случае отвергается.

Обоснования описанной процедуры те же, что и в предыдущих разделах. Из описанной процедуры следует, что исследователь имеет некоторую свободу выбора числа разрядов k , влияющего на число степеней свободы -распределения и в конечном счете на положение границы и результат проверки. Следует отметить, что это влияние не слишком велико. При разбиении области возможных значений непрерывной случайной величины (т.е. при назначении числа разрядов k) следует руководствоваться следующими соображениями:

как уже указывалось, каждый разряд должен быть в достаточной мере представительным, т.е. не должно быть пустых разрядов ( ) и разрядов с очень малыми числами наблюдений, с этой точки зрения число k должно быть невелико;

разрядов должно быть достаточно много, чтобы гистограмма хорошо аппроксимировала непрерывную кривую.

Естественно, что эти два требования противоречивы и не всегда удается в полной мере удовлетворить их.