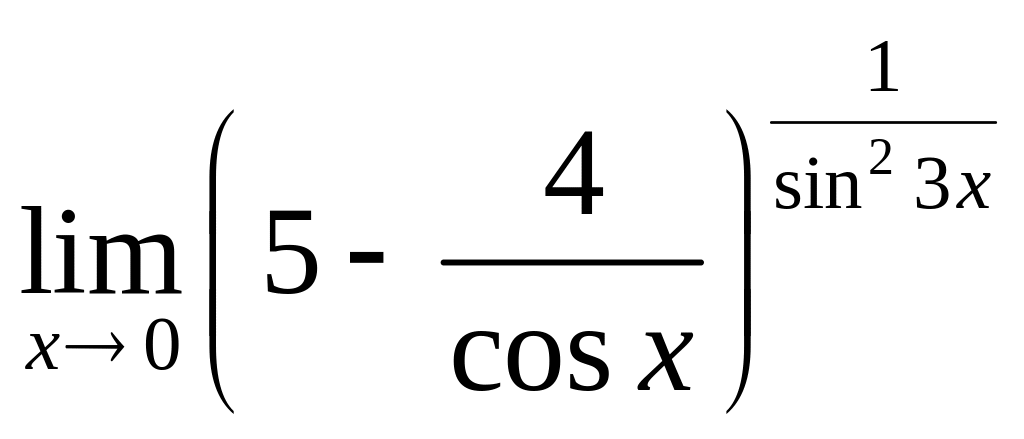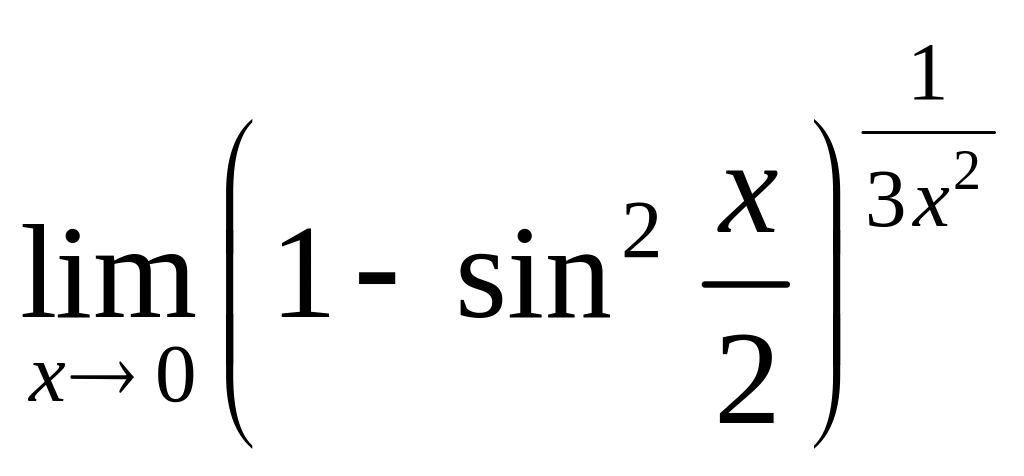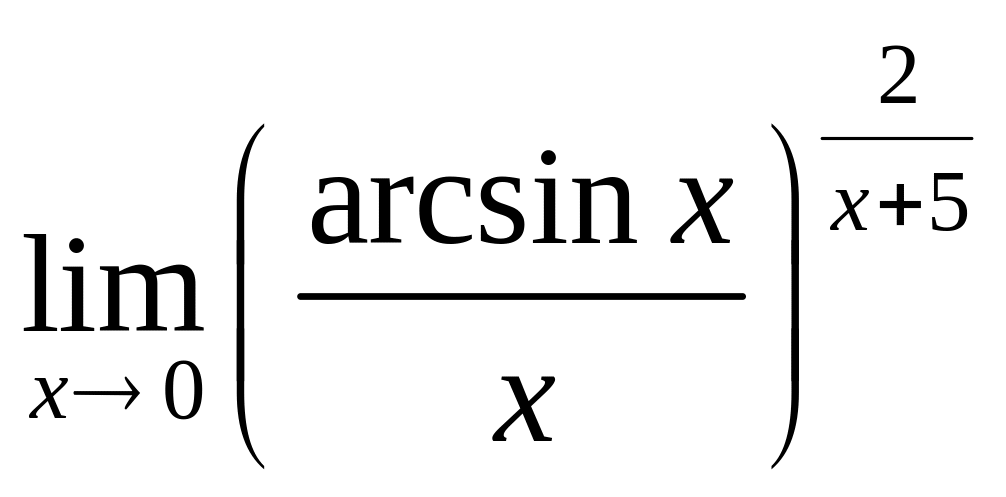Задания к вариантам для самостоятельных работ
I Упросить:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
|
II Разложить подынтегральную функцию в ряд Тейлора и вычислить определенный интеграл. Сравнить полученное значение со значением определенного интеграла вычисленного без использования разложения подынтегральной функции в ряд.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10. |
11.
|
12.
|
13.
|
14.
|
|
III Найти все корни уравнения, изобразить функцию на координатной плоскости и указать месторасположение корней
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10. |
11.
|
12.
|
13.
|
14.
|
|
IV Разложить функцию по простому аргументу х:
1. tg5x |
2. sin6x |
3. cos5x |
4. sin8x |
5. ctg7x |
6. ctg4x |
7. tg5x |
8. cos7x |
9. sin7x |
10. tg4x |
11. cos9x |
12. tg7x |
13. sin9x |
14.
|
V Вычислить пределы:
1.
а).
|
2.
а).
|
3.
а).
|
4.
а).
|
5.
а).
|
6.
а).
|
7.
а).
|
8.
а).
|
9.
а).
|
10.
а).
|
11.
а).
|
12.
а).
|
13.
а).
|
14.
а).
|
VI Вычислить неопределенный интеграл и производную подынтегральной функции
1.
|
2.
|
3.
|
4.
|
||||||
5.
|
6.
|
7.
|
8.
|
||||||
9.
|
10.
|
11.
|
12.
|
||||||
13.
|
14.
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

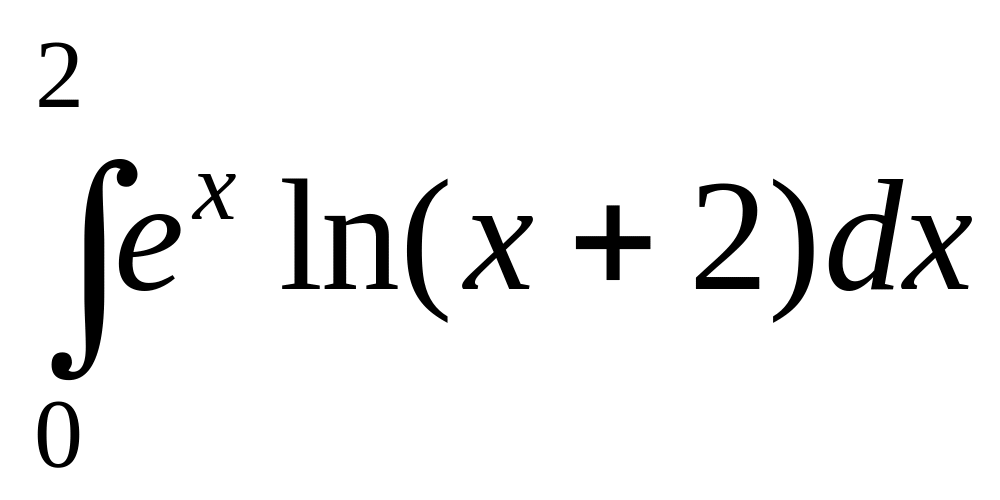

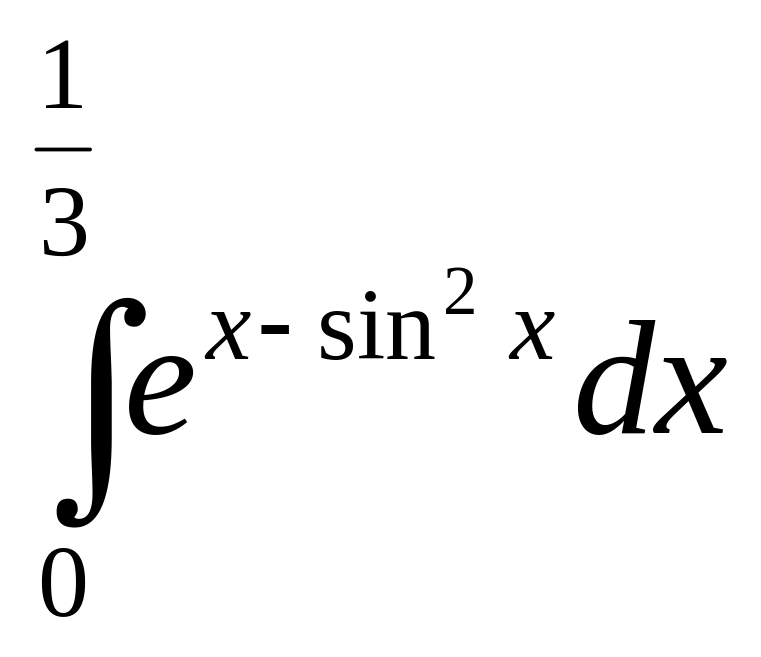
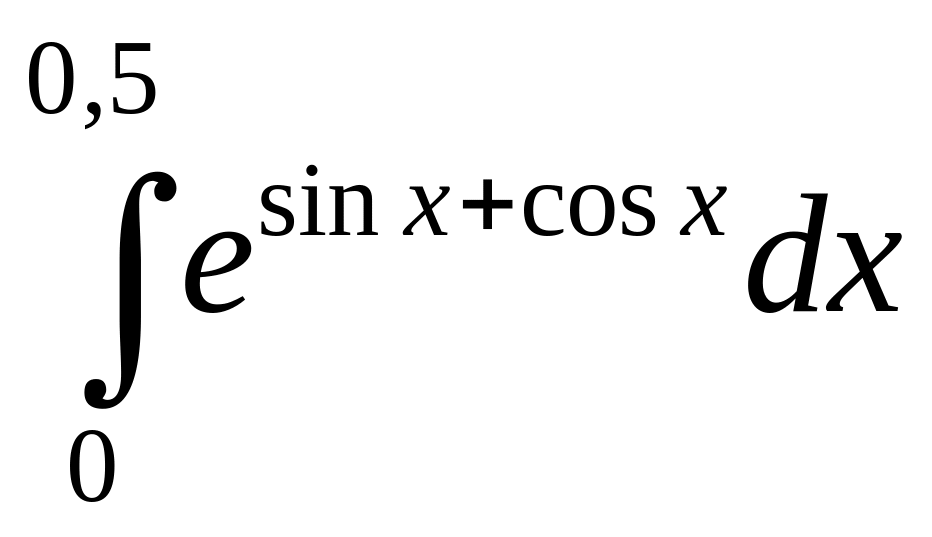
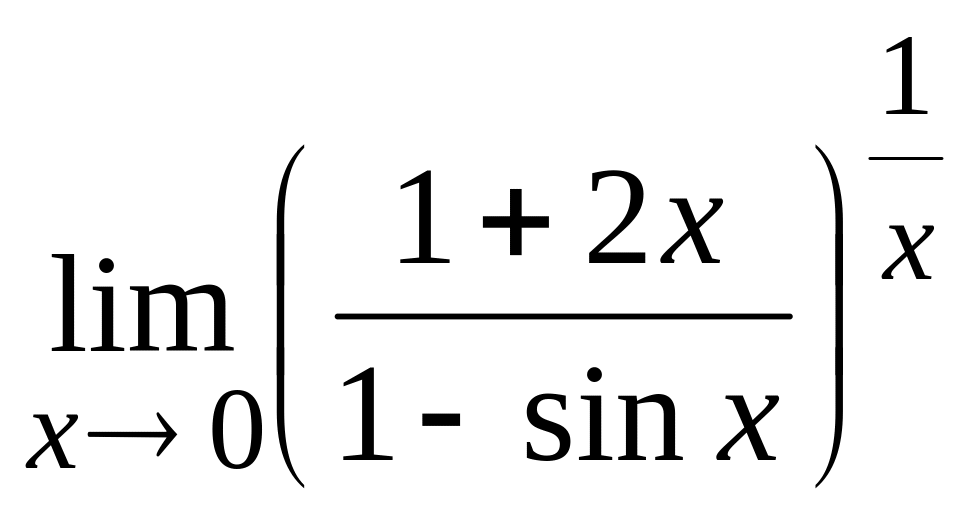
 ;
б).
;
б).

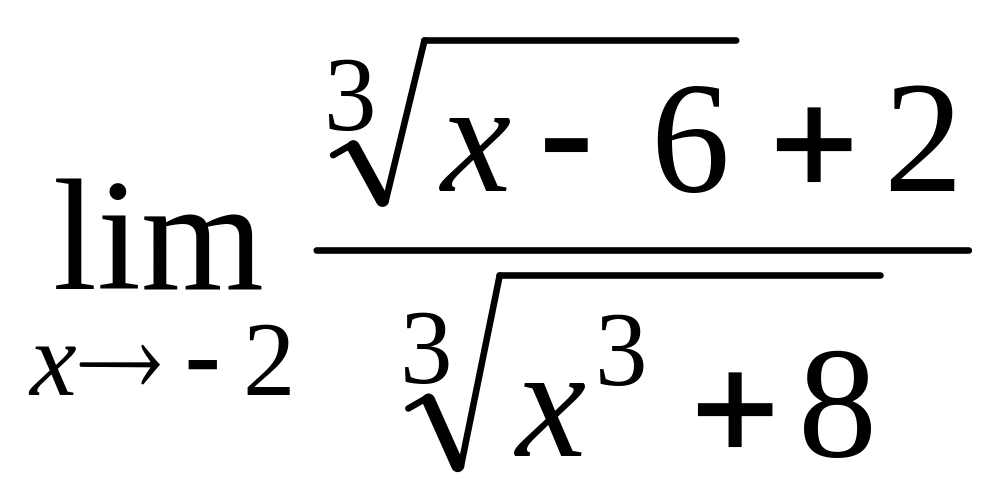 ;
б).
;
б).