ЛАБОРАТОРНАЯ РАБОТА № 4

Приближенные методы решения алгебраических уравнений. Численное дифференцирование и интегрирование. Символьные вычисления

Упрощение математических выражений

Команда Symbolics (Символьные вычисления) ► Simplify (Упростить) обеспечивает выполнение одной из самых важных символьных опера­ций, которая позволяет упрощать математические выражения, содер­жащие алгебраические и тригонометрические функции, а также выра­жения со степенными многочленами (полиномами). Упрощение означает замену сложных фрагментов выражения просты­ми. К примеру, в прежних версиях Mathcad функция tan(х) считалась более сложной, чем функции sin(x), cos(x), поэтому тангенс пред­ставлялся через соотношение этих функций.

Эта команда открывает широкие возможности для упрощения слож­ных и плохо упорядоченных алгебраических выражений. С помощью команды Simplify мож­но выполнять символьные вычисления производных и определенных интегралов, заданных соответствующими операторами.

Символьное вычисление производных

Если f(х) — непрерывная функция аргумента х, то производная этой функции определяется следующим образом: . Таким образом, производная функции f(х) — это предел, к которому стремится отношение бесконечно малого приращения функции к со­ответствующему бесконечно малому приращению аргумента . Если речь идет о вычислении численного значения производной, то оно про­изводится в некоторой точке х = х₀. Как известно, значение производ­ной геометрически характеризуется наклоном касательной к графику f(х) в точке х = х₀.

Непрерывность функции не является достаточным признаком того, что она имеет производную. Не все такие функции имеют производные во всех точках. В принципе, возможны даже непрерывные функции, во­обще не имеющие производных. Разрывные функции в точках разрыва не имеют производных, хотя возможны производные слева и справа от точек разрыва.

Производная от производной f(х), то есть функция f''(х), называет­ся производной второго порядка. Могут быть производные третьего, четвертого и т. д. порядков, словом, производные высшего порядка. Все математические системы способны вычислять такие производные, как и первую производную f'(х) от функции f(х).

Довольно часто встречаются функции нескольких переменных, напри­мер f(х, у, z ,...). В этом случае может идти речь о частных производ­ных по переменным х, у, z, и т.д.

С помощью команды Symbolics (Символьные вычисления) ► Simplify (Упростить) вполне возможно вычисление производных как первого, так и высшего порядков, заданных явно операторами дифференцирования.

Символьное вычисление интегралов

Если есть некоторая функция f(х), то показанный ниже определен­ный интеграл дает значение площади, ограниченной вертикалями а и b, именуемыми пределами интегрирования, кривой f(х) и осью абс­цисс х: 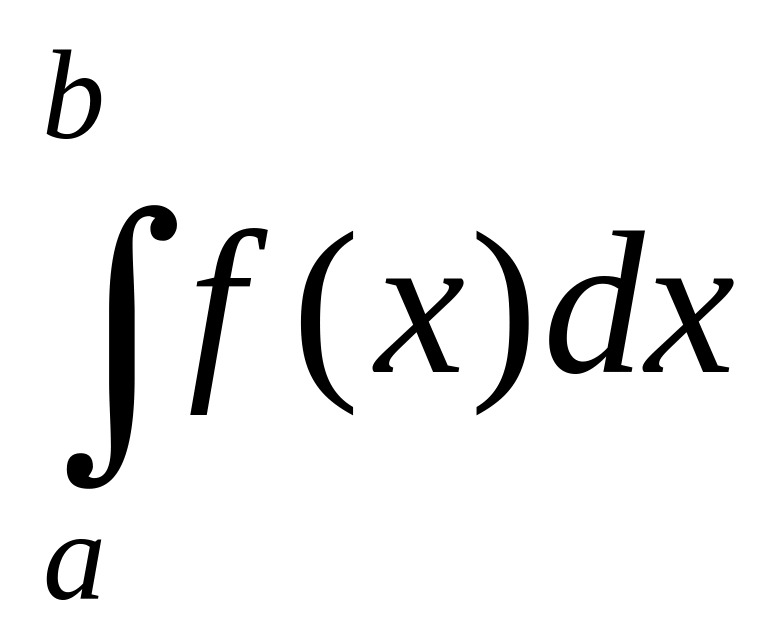. Такой интеграл обычно представляется числом (в общем случае комп­лексным), но может быть представлен и аналитическим выражением. Если f(x)dx есть дифференциал функции F(х), то f(x)dx = dF(x). Функцию F(х) называют первообразной функции f(x). Наиболее об­щий вид первообразной функции f(х) называют неопределенным ин­тегралом и обозначают следующим образом: .

В состав этого выражения обычно включается некоторая постоянная интегрирования С, подчеркивающая, что для одной и той же функции f(х) существует масса первообразных, описываемых одной и той же линией, но смещенных по вертикали на произвольную постоянную. О ее существо­вании надо помнить, так как она отдельно в результате не показывается. Возможно также вычисление кратных интегралов, например двойных.

Система Mathcad содержит встроенную функцию для вычисления значений определенных интегралов приближенным численным мето­дом. Ею целесообразно пользоваться, когда нужно просто получить зна­чение определенного интеграла в виде числа. С другой стороны, команда Symbolics (Символьные вычисления) ► Simplify (Упростить) примени­тельно к вычислениям определенных интегралов делает гораздо боль­ше — она ищет аналитическое выражение для интеграла. Более того, она способна делать это и при вычислении кратных интегралов, преде­лы которых — функции.

Как и в случае с вычислением производных, вычисление интегралов с помощью команды Simplify требует записи вычисляемых интегралов в явном виде — с применением шаблонов интегралов.

Расширение выражений

Действие команды Symbolics (Символьные вычисления) ► Expand (Раз­ложить по степеням) в известном смысле противоположно действию команды Symbolics (Символьные вычисления) ► Simplify (Упростить). Подвергаемое преобразованию выражение «расширяется» с использованием известных (и введенных в символьное ядро) соотношений. Разу­меется, расширение происходит только в том случае, когда его резуль­тат однозначен, иначе нельзя считать, что действие этой команды про­тивоположно действию команды Simplify. К примеру, команда Simplify преобразует сумму квадратов синуса и косинуса в 1, тогда как обратное преобразование многозначно и потому в общем виде невыполнимо.

При преобразовании выражений командой Expand система старается более простые функции представить через более сложные, свести ал­гебраические выражения, представленные в сжатом виде, к выражени­ям в развернутом виде и т. д.

Разложение выражений

Команда Symbolics (Символьные вычисления) ► Factor (Разложить множители) используется для факторизации — разложения выраже­ний или чисел на простые множители. Она способствует выявлению математической сущности выражения, например наглядно выявляет представление полинома через его действительные корни, а в том слу­чае, когда разложение части полинома содержит комплексно-сопряжен­ные корни, порождающее их выражение представляется квадратичным трехчленом. В большинстве случаев (но не всегда) операция факторизации ведет к упрощению выражений. Термин «факторизация» не является общепри­знанным в отечественной математической литературе, но мы его остав­ляем в связи с созвучностью англоязычному названию этой операции.

В Mathcad разложение чисел на простые множители записывает­ся как произведение множителей, причем повторяющиеся п раз мно­жители записываются в степени п.

Разложение по подвыражениям

Команда Symbolics (Символьные вычисления) ► Collect (Разложить по подвыражениям), полное название которой «Collect on Subexpresion», обеспечивает замену указанного выражения выражением, скомплекто­ванным по базису указанной переменной, если такое представление воз­можно. Эта команда особенно удобна, когда заданное выражение есть функция ряда переменных и нужно представить его в виде функции заданной переменной, имеющей вид степенного многочлена. При этом другие переменные входят в сомножители указанной переменной, пред­ставленные в порядке уменьшения ее степени. В том случае, когда комплектование по базису указанной переменной невозможно, система выдает сообщение об этом (снизу на рисунке).

Подстановка

Команда Symbolics (Символьные вычисления) ► Variable (Перемен­ная) ► Substitute (Подставить) возвращает новое выражение, получен­ное путем подстановки вместо указанной переменной некоторого другого выражения. Последнее должно быть подготовлено и помещено в [буфер обмена командой Cut (Вырезать) или Сору (Копировать) меню Edit (Правка). Наряду с получением результата в символьном виде эти команды позволяют найти и численные значения функции некоторой переменной путем замены ее аргумента числовым значением. Подстановка и замена переменных довольно часто встречаются в математических расчетах, что делает эти команды весьма полезными. Кроме того, они дают возможность перейти от символьного представления результата к числовому.

Разложение в ряд Тейлора

Команда Symbolics (Символьные вычисления) ► Variable (Переменная) ► Expand to Series (Разложить в ряд) выполняет разложение выражения в ряд Тейлора относительно выделенной переменной с заданным по зап­росу числом членов ряда п (число определяется по степеням ряда). Такое разложение относительно точки х = х₀ функции f(x) имеет вид:

.

Если разложение выполняется относительно точки х = 0, его принято называть рядом Маклорена: . По умолчанию принимается п = 6. Разложение возможно для функ­ции заданной переменной. В разложении указывается остаточная по­грешность.

Команда Expand - разлагает функцию по простым степеням, по простому аргументу.

Символьные операции нередко можно комбинировать для решения сложных задач — задачи вычисления определенного интеграла, который не бе­рется в явном виде.

Если пользователя (например; инженера) интересует просто числен­ное значение интеграла, надо лишь поставить после интеграла знак вывода = и значение интеграла будет вычислено адаптивным численным методом Симпсона. Однако попытка вычислить такой интеграл с помощью команды Symbolics (Символьные вычисления) ►Simplify (Упростить) окажется неудачной: после долгих попыток система сооб­щит, что интеграл в явном виде не берется.

Прием заключается в замене подынтегральной функции ее разложением в ряд Тейлора. Вначале необходимо получить такое разложение с избытком — для 10 членов ряда (однако учтенных нечетных членов тут нет, такова специфика функции). Далее, выделив четыре первых реальных члена и используя команды Сору (Ко­пировать) и Paste (Вставить) меню Edit (Правка), поместить это разложение на место шаблона подынтегральной функции. Теперь проблем с вычислением интеграла с помощью команды Simplify не будет.

Интеграл получается в форме ехр(), помноженной на дробные мно­жители, представленный в рациональной форме (отношения целых чисел). Это обстоятельство, возможно, бесполезное для рядового пользователя, наверняка будет весьма положительно воспринято «ис­тинным» математиком, поскольку здесь напрашиваются определенные аналитические выводы, которые нельзя сделать при вычислении ин­теграла численными методами.

Решение уравнений

Если задано некоторое выражение F(x) и выделена переменная х, ко­манда Symbolics (Символьные вычисления) ► Variable (Переменная) ► Solve (Решить) возвращает символьные значения указанной перемен­ной х, при которых F(x) = 0. Это очень удобно для решения алгебраи­ческих уравнений, например квадратных и кубических, а также для вычисления корней полинома.

С помощью команды Paste (Вставить) меню Edit (Правка) можно пере­нести решение в основное окно системы, но оно окажется текстовым комментарием (а не частью математического выражения) и не будет пригодно для дальнейших преобразований. Впрочем, часть решения (опять-таки через буфер обмена) можно ввести в формульные блоки для последующих преобразований и вычислений. Если при решении квадратного уравнения получены про­стые выражения, известные даже школьникам, то при увеличении порядка уравнения всего на единицу ре­зультаты представляются весьма громоздкими и малопригодными для анализа формулами. Хорошо еще, что существующими!

Пользователю надо реально оце­нить свои силы в упрощении решения. Это придется сделать «вруч­ную». При технических расчетах специалист нередко знает, какие из параметров решения несущественны, и может их отбросить. Однако для строгих математических расчетов это не всегда возможно, поэтому даже громоздкий результат может быть весьма полезным с познавательной точки зрения.