4. Циклический алгоритм

В жизни, однако, часто встречаются инструкции, в которых требуется один и тот же набор действий выполнять много раз подряд: "Иди, пока не придешь", "Закручивай гайку, пока не завернешь до отказа" и так далее. Используя только ветвление, такие алгоритмы записать не удастся. Для этого нужна новая форма организации действий – цикл. Если какие-либо операторы необходимо выполнить несколько раз, то их не переписывают каждый раз заново, а организуют цикл.

Циклический алгоритм – это алгоритм, в котором некоторая последовательность действий повторяется несколько раз.

1. Алгоритм заточки карандашей 2. Алгоритм просмотра телевизора

5.Виды циклов

1. Цикл с предусловием (цикл пока)

Телом цикла называются команды, многократно повторяющиеся в процессе его выполнения. Перед выполнением цикла происходит присваивание начальных значений переменным, меняющимся в ходе его выполнения. Собственно выполнение цикла Пока начинается с проверки условия его окончания. Поэтому такую разновидность цикла называют еще циклом с предусловием. Переход к выполнению тела цикла, включающего в себя рабочий блок и изменение значений аргументов, осуществляется только в том случае, если условие выполняется. В противном случае происходит выход из цикла. В частности, может оказаться, что тело цикла не будет выполнено ни разу (если с самого начала условие не выполняется). С другой стороны, для того чтобы цикл не повторялся бесконечно, необходимо в теле цикла осуществлять действия, приводящие к ситуации, когда условие перестанет быть истинным. Этой цели и служит блок изменения значений аргументов.

2. Цикл с постусловием (цикл до)

Цикла с заранее неизвестным числом повторений. Здесь условие выполнения цикла проверяется в конце выполнения тела цикла, то есть в любом случае тело цикла будет выполнено хотя бы один раз. Цикл До называют циклом с постусловием потому что выполняется тело цикла а потом проверяется условие.

3. Арифметический цикл (цикл для) – цикл с параметром.

В том случае, когда количество повторений заранее известно, используется цикл Для. Здесь само условие выполнения цикла содержит информацию о том, сколько раз надо повторить его выполнение, например, в виде диапазона изменения цикловой переменной. Цикл для называют арифметическим циклом

Цикл с предусловием (цикл ПОКА)	Цикл с постусловием (цикл ДО)	Цикл с параметром (цикл ДЛЯ)
пока условие, повторять нц серия кц	повторять серия до условие	для параметр от начзнач до конзнач шаг значение нц серия кц
Выполнение тела цикла повторяется, пока ус­ловие цикла истинно. Когда условие становится ложным, цикл заканчивает выполнение. Служебные слова нц и кц обозначают начало цикла и конец цикла соответственно.	Здесь используется условие окончания цикла. Когда оно стано­вится истинным, цикл заканчивает работу.	Цикл выполняется последовательно от начального значения до конечного с указанным шагом.

Пример 1. Дана последовательность, общий член которой определяется формулой

Вычислить при n 2 сумму тех ее членов, которые больше заданного числа .

Решение: При решении задачи находится очередной член последовательно и, если он больше , добавляется к сумме.

2	алг предусловие вещ , S, A, n нач Ввод S:= 0 A:= 1/4 n:= 2 пока A> , повторять нц S:= S + A A:= (n-1)/(n*n) n:= n + 1 кц Вывод S Кон

Этот алгоритм имеет циклическую структуру. В алгоритме исполь­зована структурная команда цикл-пока, или цикл с предусловием.

Для проверки правильности алгоритма строят трассировочную таблицу, в которой для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм.

Пусть =0,15, тогда

S	A	n	A>
0	1/4=0.25	2	+
1/4	2/9=0.22	3	+
1/4+2/9=0.25+0.22=0.47	3/16=0.19	4	+
0.47+0.19=0.66	4/25=0.16	5	+
0.66+0.16=0.82	5/36=0.14	6	-

Вывод: тело цикла повториться три раза при =0,15 и на выходе S=0,82

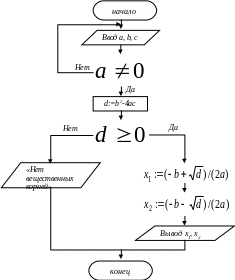
Цикл с предусловием — это основная, но не единственная форма организации циклических алгоритмов. Другим вариантом является цикл с постусловием. Рассмотрим алгоритм решения квадратного уравнения. К нему можно подойти с такой позиции: если а = 0, то это уже не квадратное уравнение и его можно не рассматривать. В таком случае будем считать, что пользователь ошибся при вводе данных, и следует предложить ему повторить ввод. Иначе говоря, в алгоритме будет предусмотрен контроль достоверности исходных данных с предоставлением пользователю возможности исправить ошибку. Наличие такого контроля — еще один признак хорошего качества программы.

алг квадратное уравнение

вещ а,b,с,d,xl,х2

нач

повторять

ввод а,b,с

до а О

d:=b²-4ac

если d 0

то

вывод xl,х2

иначе

вывод «Нет

вещественных корней»

кв

кон

В рассмотренных выше примерах количество повторений заранее неизвестно. В тех же случая, когда количество шагов известно из условия задачи, проще и предпочтительней использовать цикл с параметром.

Пример 3. Найти произведение первых k натуральных чисел, кратных трём.

При составлении алгоритма учтем, что первое натуральное число, кратное 3, есть тройка, а все последующие больше предыдущего на 3.

алг пример 3 цел k, p, t, i нач ввод k p:=1 {здесь накапливаем произведение} t:=0 {здесь будут числа, кратные 3} i:=1 для i>k нц t:=t+3 p:=p*t i:=i+1 кц вывод p Кон

Пример 4. Даны два на­туральных числа М и N. Требуется вычислить их наибольший об­щий делитель — НОД(М, N).

Эта задача решается с помощью метода, известного под назва­нием алгоритма Евклида. Его идея основана на том свойстве, что если М >N, то НОД(М, N) - НОД(М-N, N). Другой факт, лежащий в основе алгоритма, тривиален — НОД(М, М) = М. Для «ручного» выполне­ния этот алгоритм можно описать в форме следующей инструкции:

1. Если числа равны, то взять их общее значение в качестве ответа; в противном случае продолжить выполнение алгоритма.

2. Определить большее из чисел.

3. Заменить большее число разностью большего и меньшего значений.

4. Вернуться к выполнению пункта 1.

Блок-схема и алгоритм на АЯ будут следующими:

алг Евклид

цел M,N

нач ввод M,N

пока M N, повторять

нв если M>N

то M:=M-N

иначе N:=N-M

кв

кон

Алгоритм имеет структуру цикла с вложенным ветвлением. Проделайте самостоятельно трассировку этого алгоритма для случая М = 18, N = 12. В результате получится НОД = 6, что, очевидно, верно.

Самостоятельная работа:

1. Вывести на экран квадраты всех четных чисел от 3 до N.

2. Вкладчик внес в банк S руб под N% годовых. Определить сколько денег он получит через M лет.

Перечень источников:

1. Кинг Д. Создание эффективного программного обеспечения. –М.: мир, 1991 – 284с.

2. Немнюгин С.А. Turbo Pascal: учебник – СПб «Питер», 2007.- 455с.

3. Попов В.Б. Turbo Pascal для школьников. – М.: Финансы и статистика, 2009. – 525с.