
- •Часть 2
- •2011-2012 Учебный год
- •I. Программа дисциплины «Математический анализ. Часть 2»
- •IV. Интегральное исчисление функций одной переменной
- •V. Дифференциальное исчисление функции нескольких переменных
- •VI. Интегральное исчисление функций нескольких переменных
- •VII. Ряды
- •II. Структура зачета
- •Методика расчета зачетных баллов
- •III. Содержание зачета Теоретические вопросы (а)
- •Теоретические вопросы (б) Интегральное исчисление
- •Дифференциальное исчисление функции нескольких переменных
- •Интегральное исчисление функций нескольких переменных
- •Примеры задач
- •1.Интегральное исчисление функции одной переменной
- •2. Дифференциальное исчисление функции нескольких переменных
- •3. Интегральное исчисление функций нескольких переменных
- •IV. Образцы билетов для зачета Вариант 1
- •Вариант 2
- •V. Ответы Примеры задач
- •1.Интегральное исчисление функции одной переменной
- •2. Дифференциальное исчисление функции нескольких переменных
- •3. Интегральное исчисление функций нескольких переменных
- •Образцы экзаменационных билетов
- •VI. Рекомендуемая литература
Теоретические вопросы (б) Интегральное исчисление
Докажите, что если
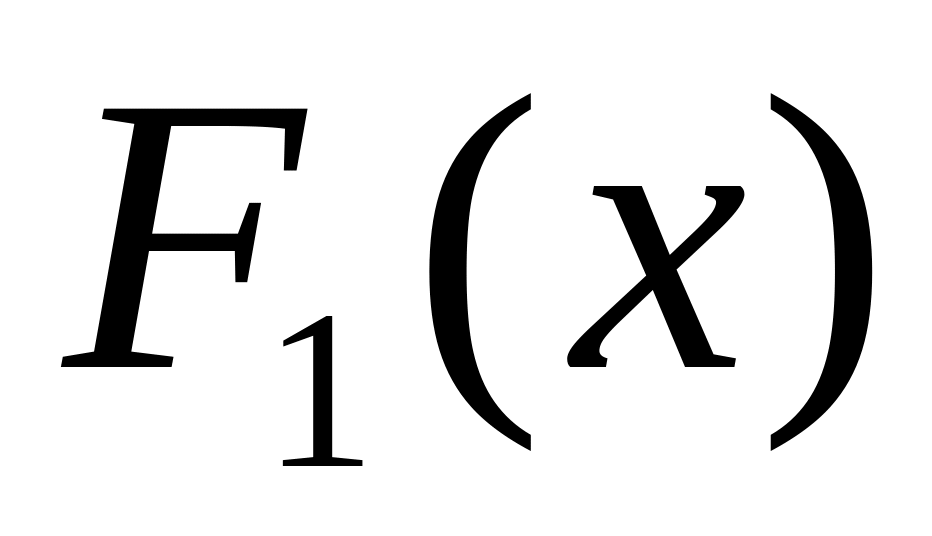 и
и
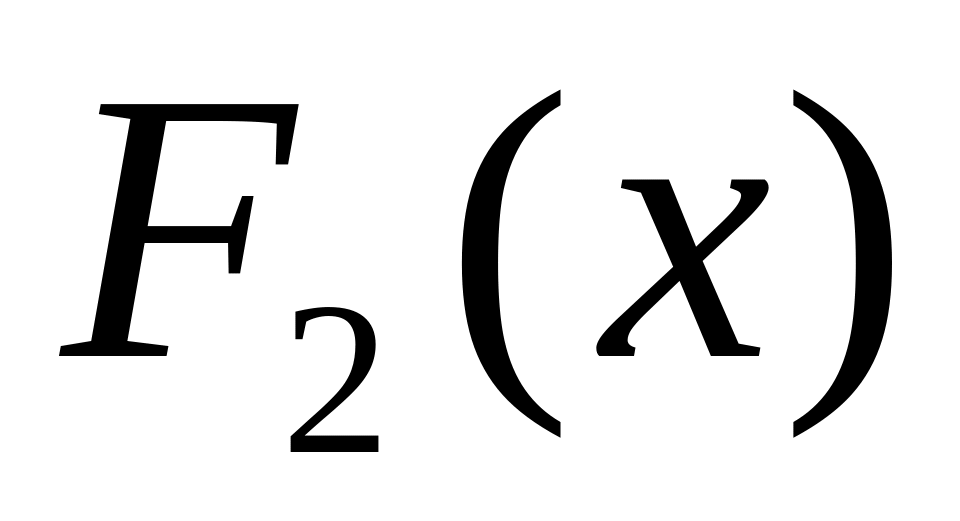 –
первообразные функции
–
первообразные функции
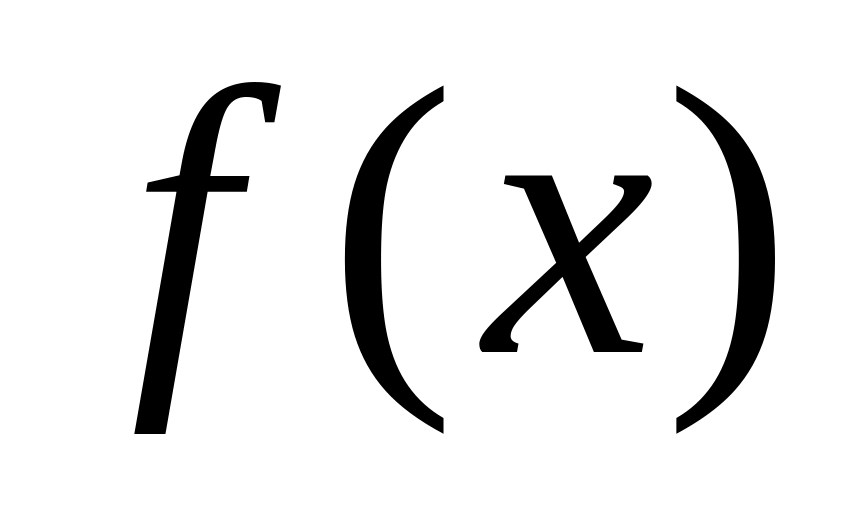 на интервале
на интервале
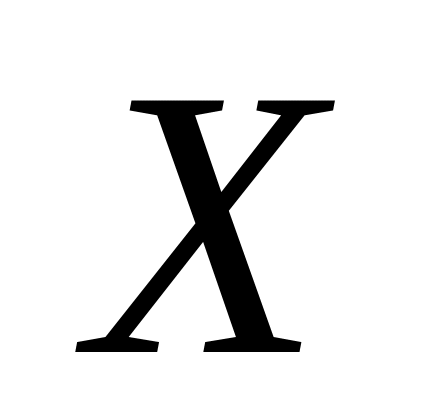 ,
то
,
то
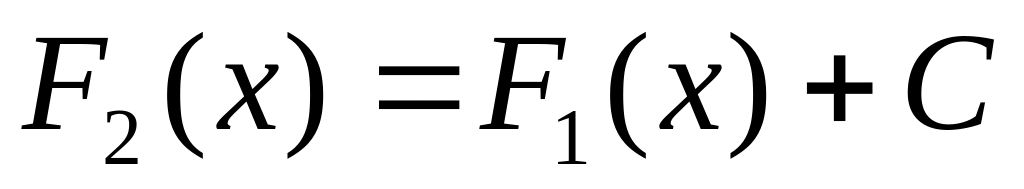 ,
где
,
где
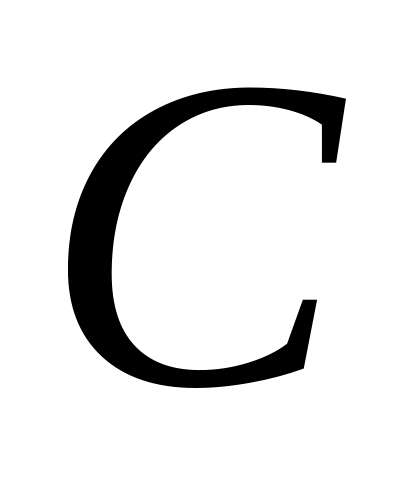 –
некоторая постоянная.
–
некоторая постоянная.
Докажите, что
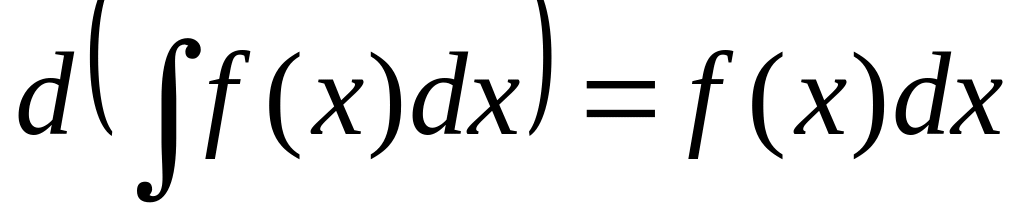 .
.
Докажите формулу интегрирования по частям для неопределенного интеграла.
Докажите формулу замены переменной для неопределенного интеграла.
Докажите, что если функция непрерывна на отрезке
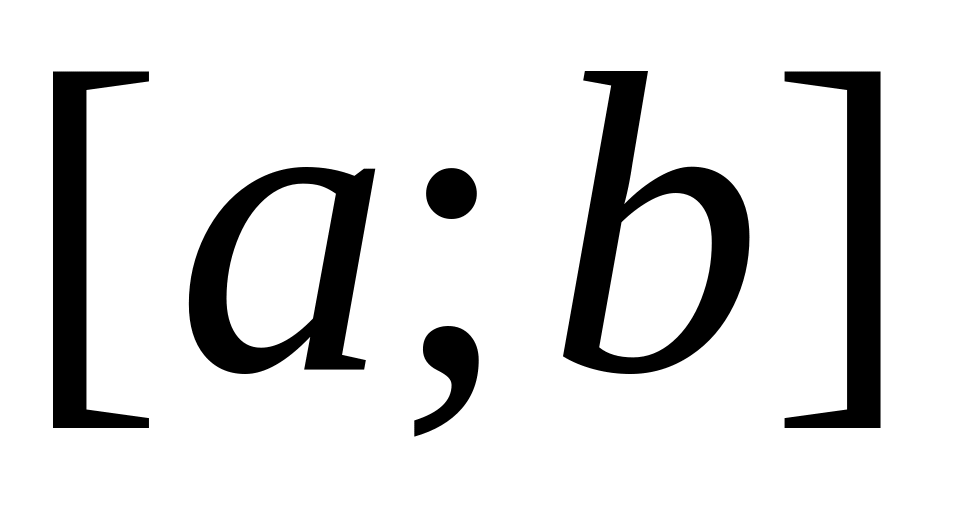 ,
то функция
,
то функция
 ,
,
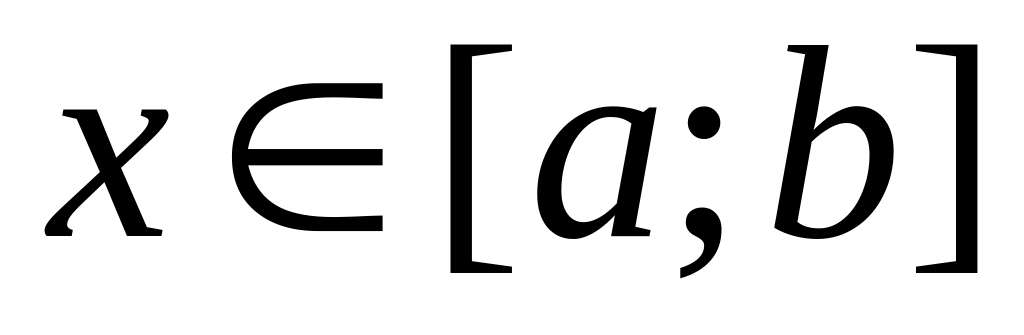 ,
является ее первообразной на этом
отрезке.
,
является ее первообразной на этом
отрезке.Используя свойство интеграла с переменным верхним пределом, докажите формулу Ньютона-Лейбница.
Применив замену переменной в определенном интеграле, докажите, что для любой четной непрерывной на отрезке
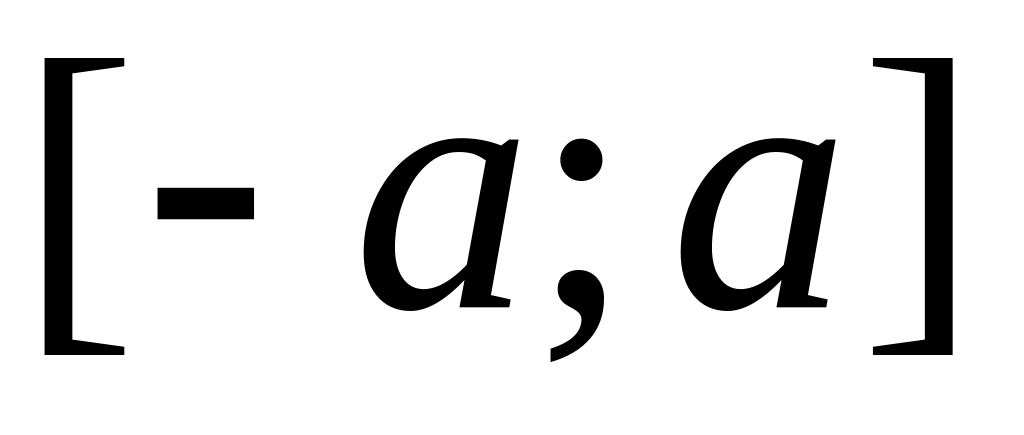 функции
справедливо
равенство
функции
справедливо
равенство
 .
В чем состоит его геометрический смысл?
.
В чем состоит его геометрический смысл?
Применив замену переменной в определенном интеграле, докажите, что для любой нечетной непрерывной на отрезке функции справедливо равенство
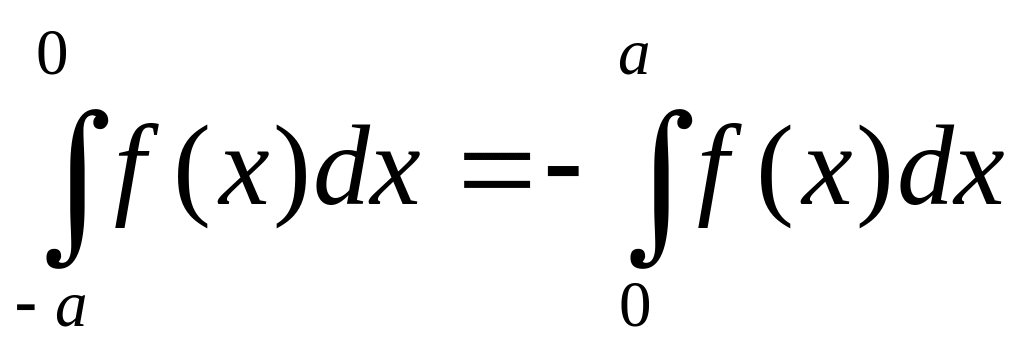 .
В чем состоит его геометрический смысл?
.
В чем состоит его геометрический смысл?
Сходится ли интеграл
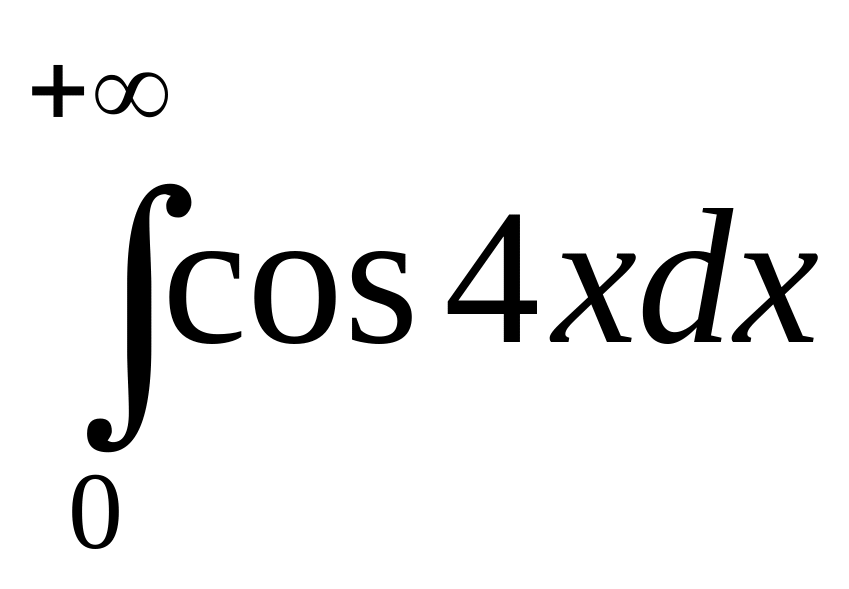 ?
Ответ обоснуйте.
?
Ответ обоснуйте.
Сходится ли интеграл
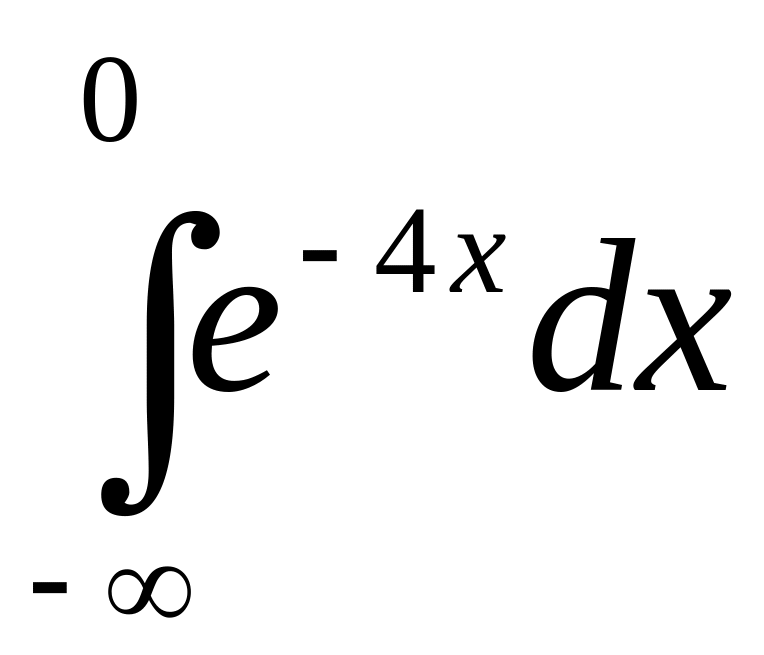 ?
Ответ обоснуйте.
?
Ответ обоснуйте.
При каких значениях
 сходится интеграл
сходится интеграл
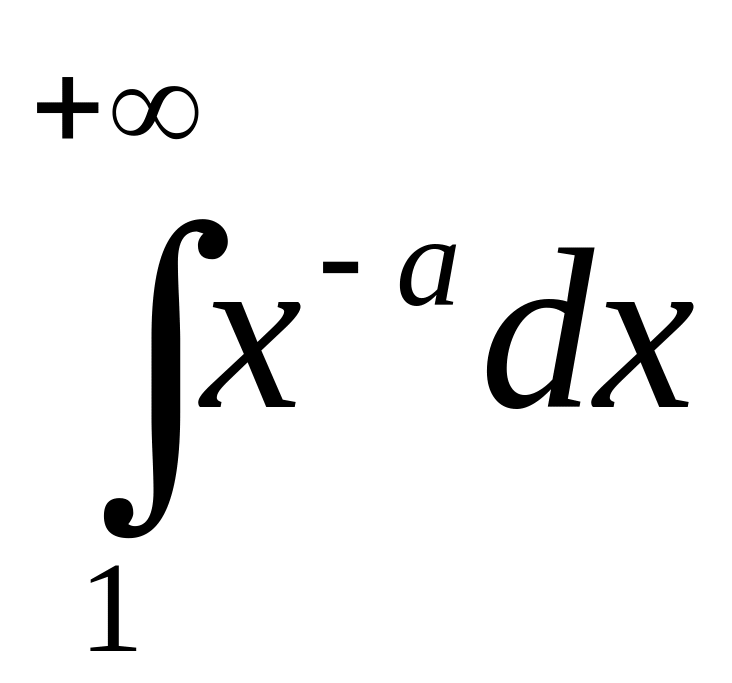 ?
Ответ обоснуйте.
?
Ответ обоснуйте.
Сходится ли интеграл
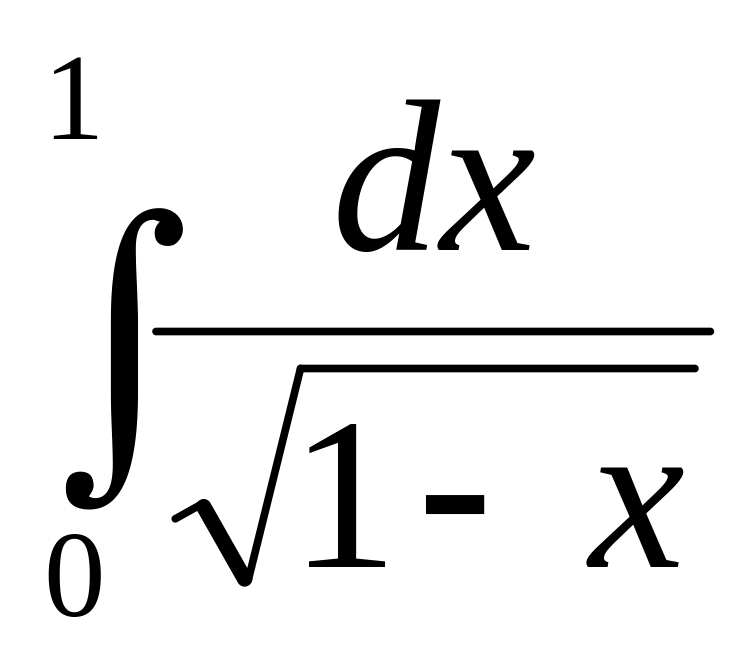 ?
Ответ обоснуйте.
?
Ответ обоснуйте.При каких значениях
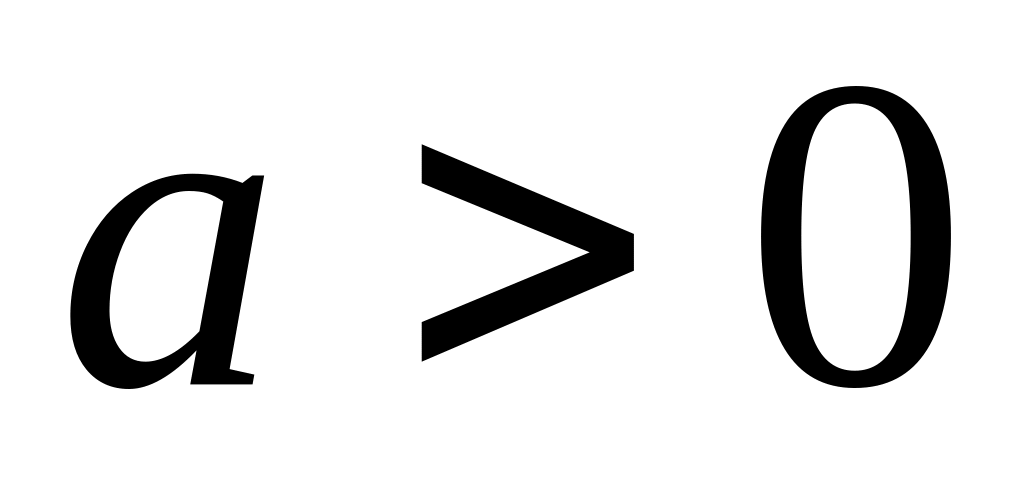 сходится
интеграл
сходится
интеграл
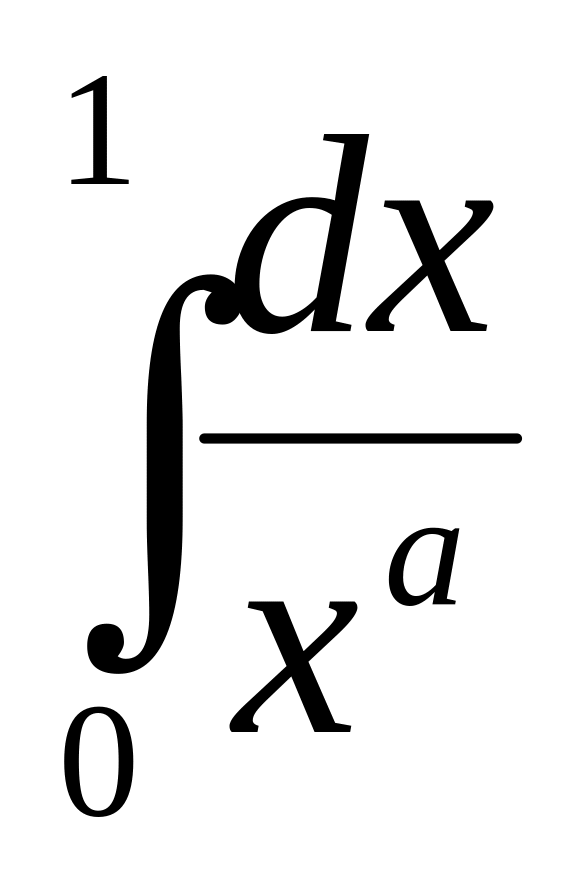 ?
Ответ обоснуйте.
?
Ответ обоснуйте.
Дифференциальное исчисление функции нескольких переменных
Дайте определение расстояния
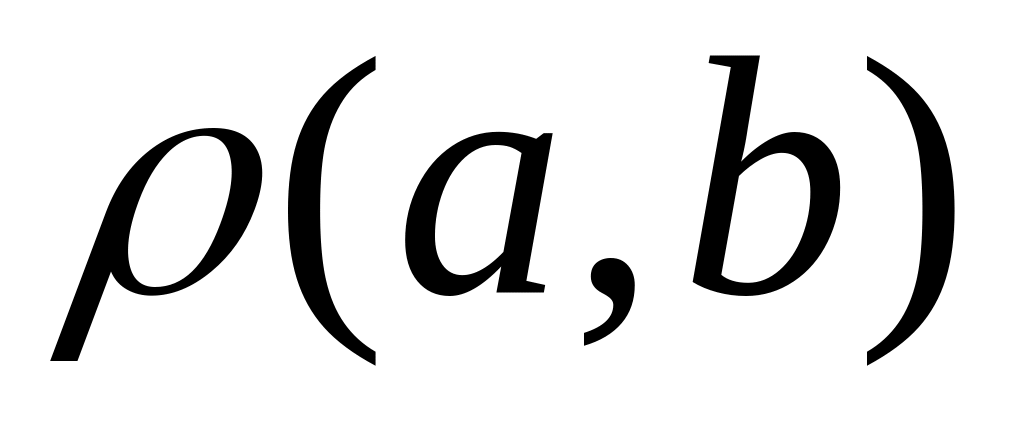 между точками
между точками
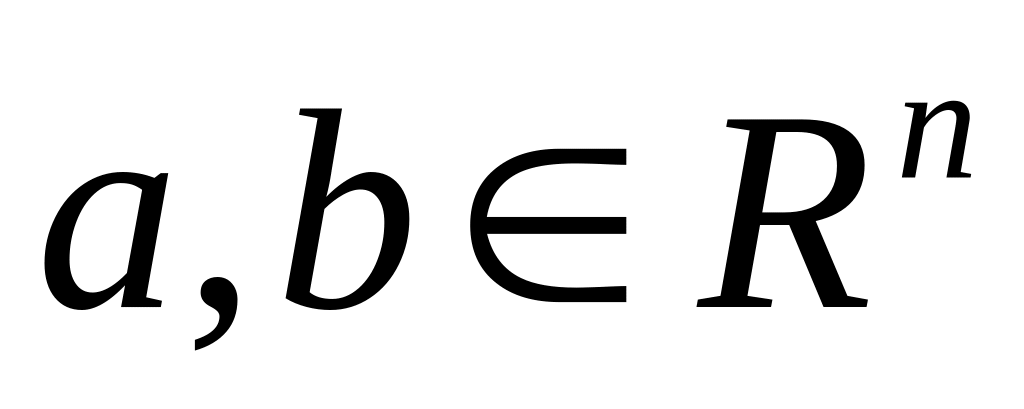 .
Сформулируйте и докажите свойства
функции
.
.
Сформулируйте и докажите свойства
функции
.Дайте определение открытого множества в
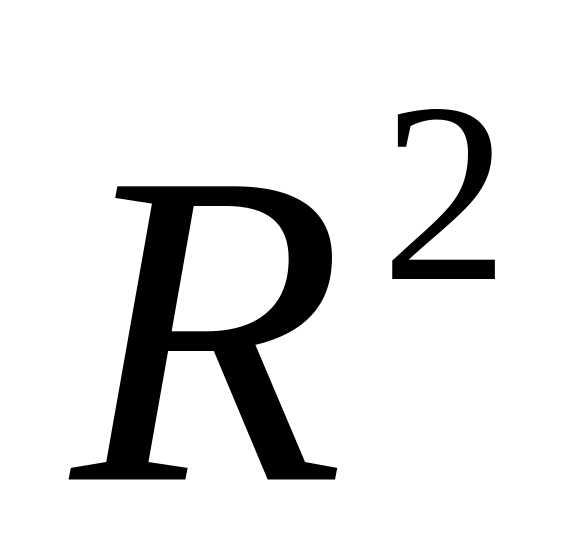 .
Является ли множество
.
Является ли множество
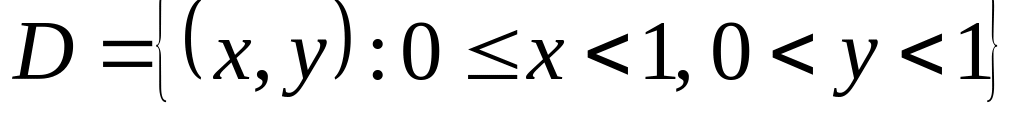 открытым? Ответ обоснуйте.
открытым? Ответ обоснуйте.
Дайте определение замкнутого множества в . Является ли множество
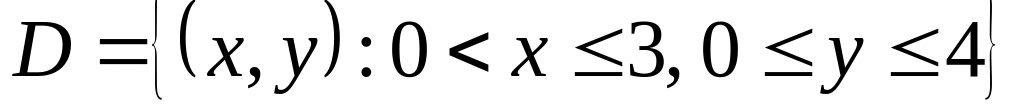 замкнутым? Ответ обоснуйте.
замкнутым? Ответ обоснуйте.
Дайте определение открытого множества в . Является ли множество
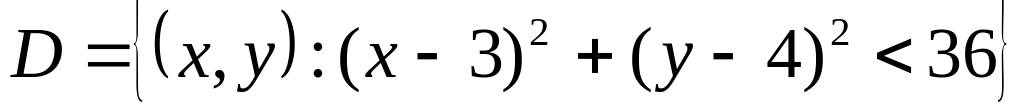 открытым? Ответ обоснуйте.
открытым? Ответ обоснуйте.Дайте определение предельной точки множества. Приведите примеры: а) множества, содержащего все свои предельные точки, б) множества, для которого существует предельная точка, ему не принадлежащая.
Дайте определение сходящейся последовательности точек в
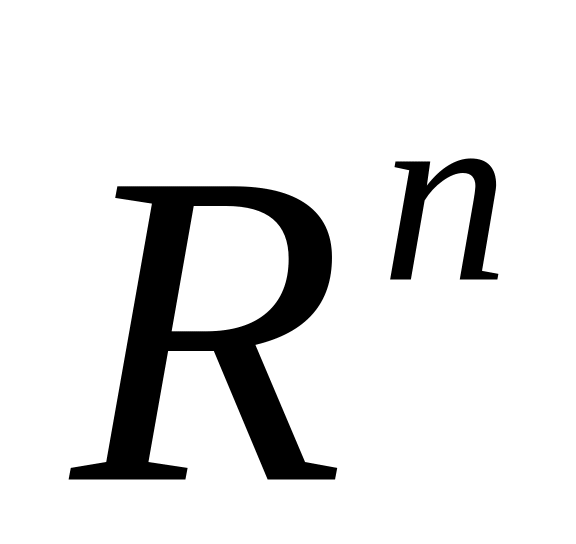 .
К какой точке в
сходится последовательность
.
К какой точке в
сходится последовательность
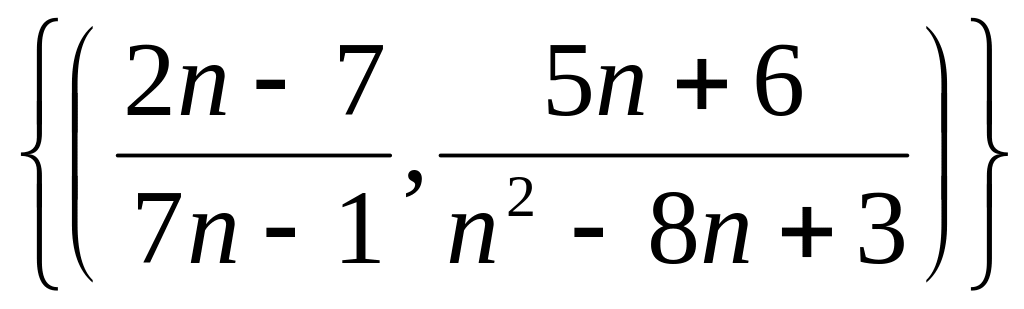 ?
Ответ обоснуйте.
?
Ответ обоснуйте.
Дайте определение сходящейся последовательности точек в
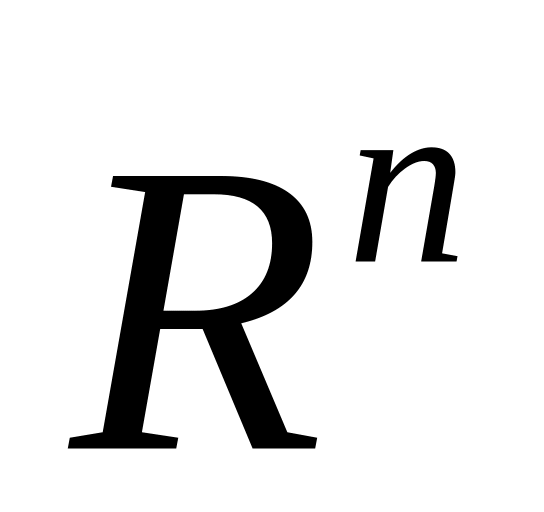 .
К какой точке в
сходится последовательность
.
К какой точке в
сходится последовательность
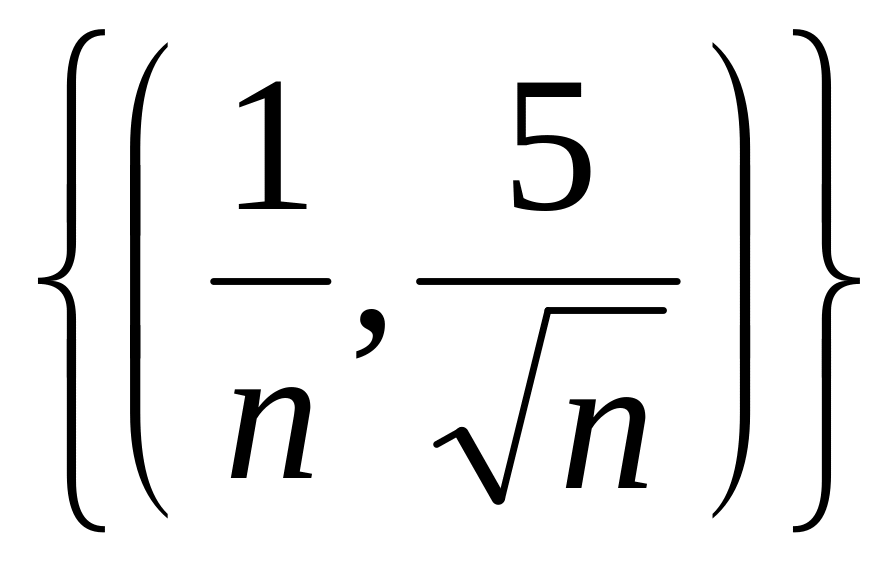 ?
Ответ обоснуйте.
?
Ответ обоснуйте.Дайте определение предела функции двух переменных в точке. Найдите предел функции
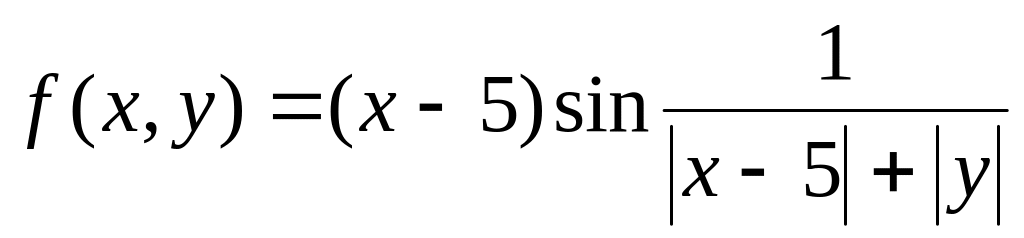 в точке
в точке
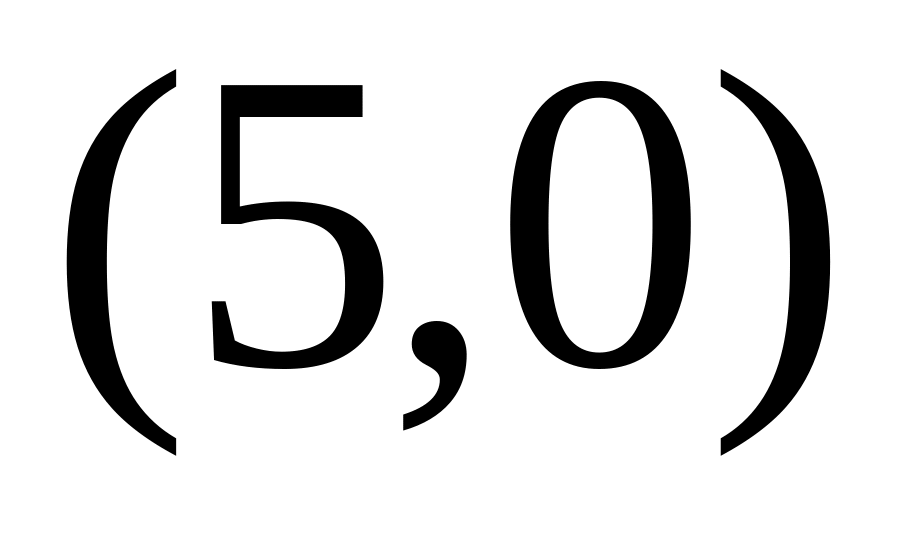 .
Ответ обоснуйте.
.
Ответ обоснуйте.
Дайте определение предела функции двух переменных в точке. Докажите, что функция
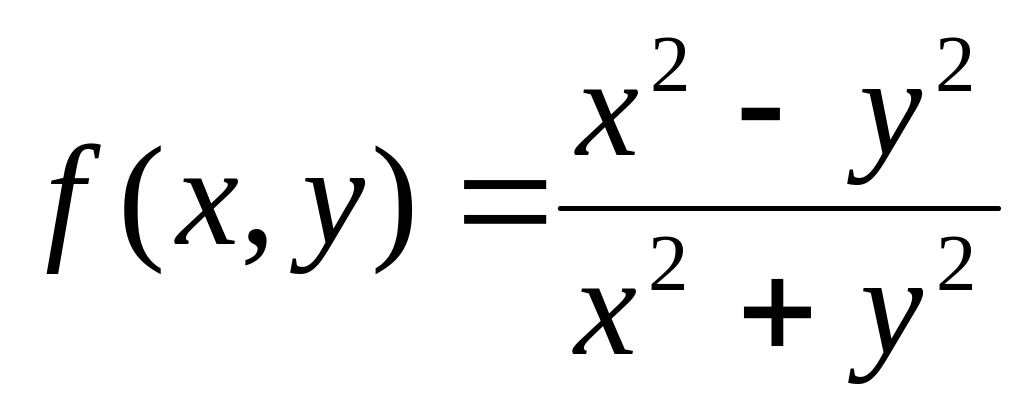 не имеет предела в точке
не имеет предела в точке
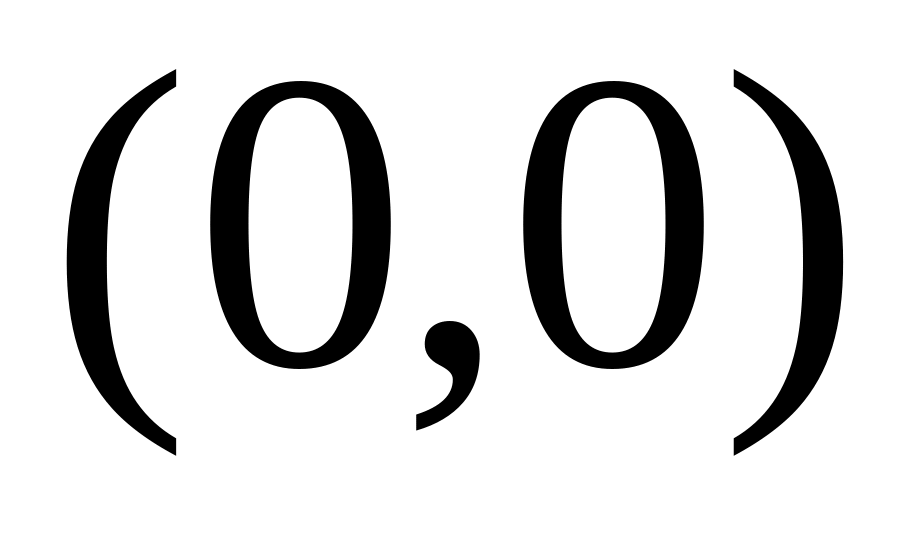 .
.Дайте определение функции двух переменных, непрерывной в точке. Является ли функция
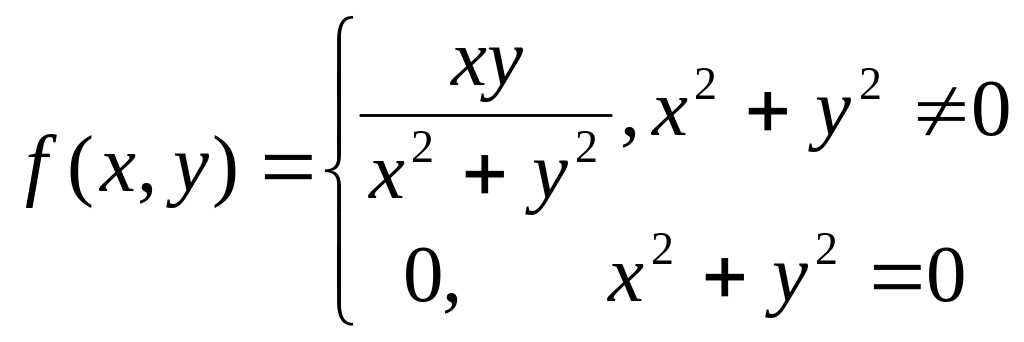 непрерывной
в точке
?
Ответ обоснуйте.
непрерывной
в точке
?
Ответ обоснуйте.
Докажите, что функция
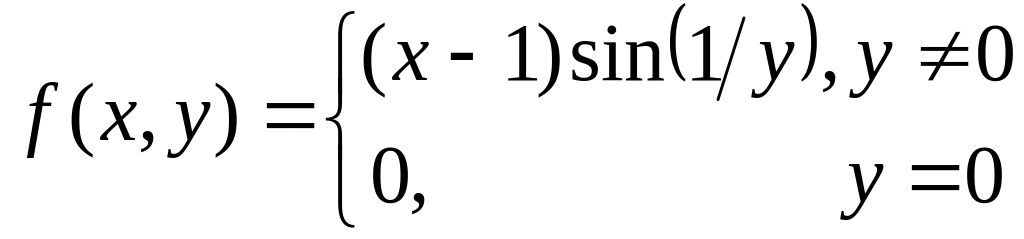 непрерывна в точке
непрерывна в точке
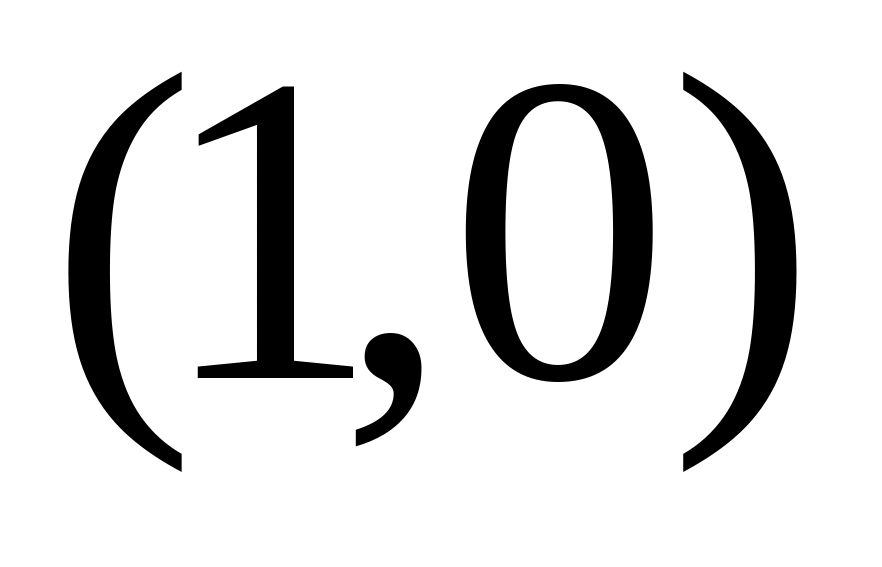 .
.Дайте определение частной производной функции
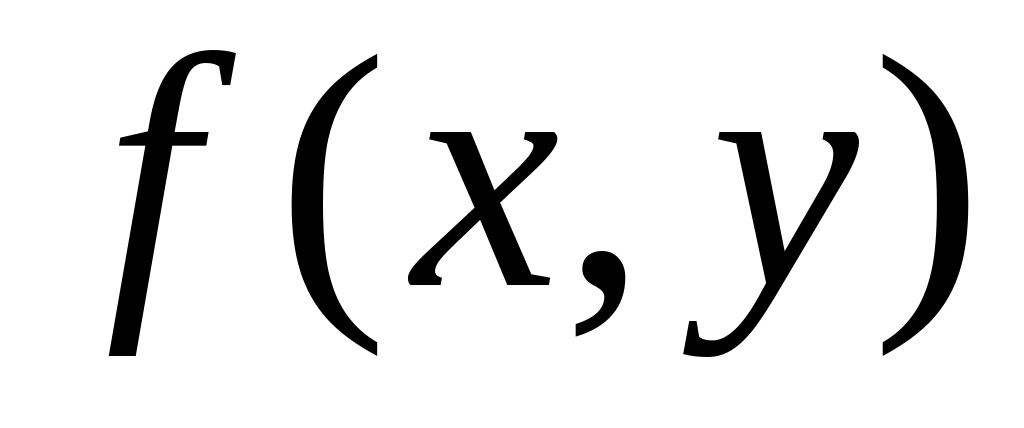 по
по
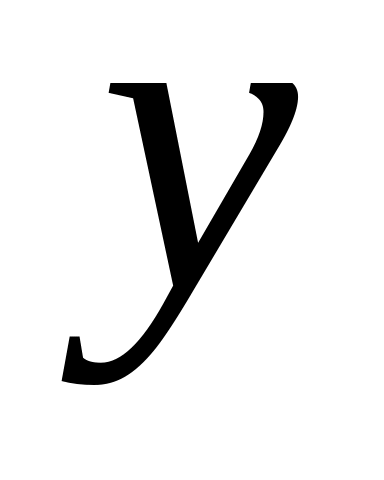 в точке
в точке
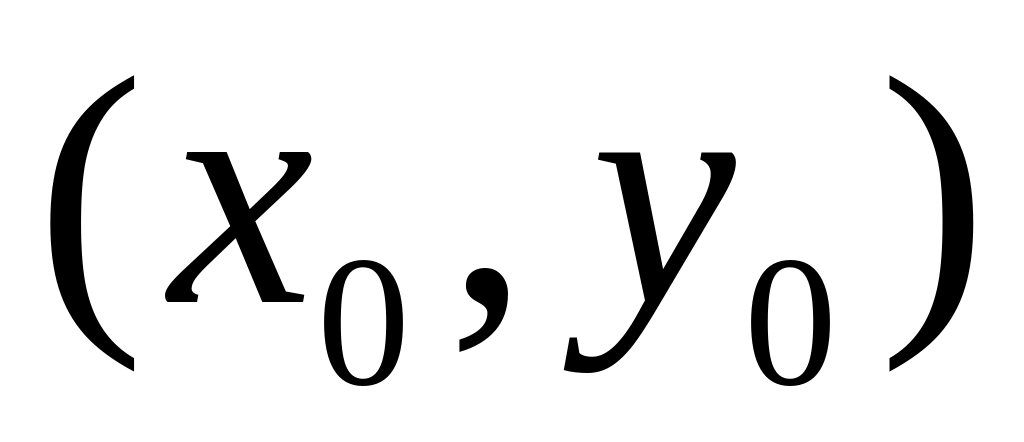 .
Найдите
.
Найдите
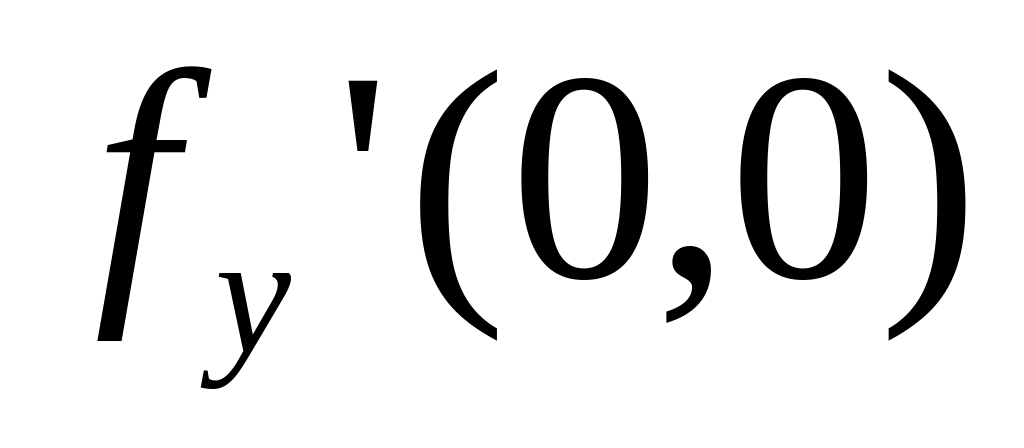 ,
если
,
если
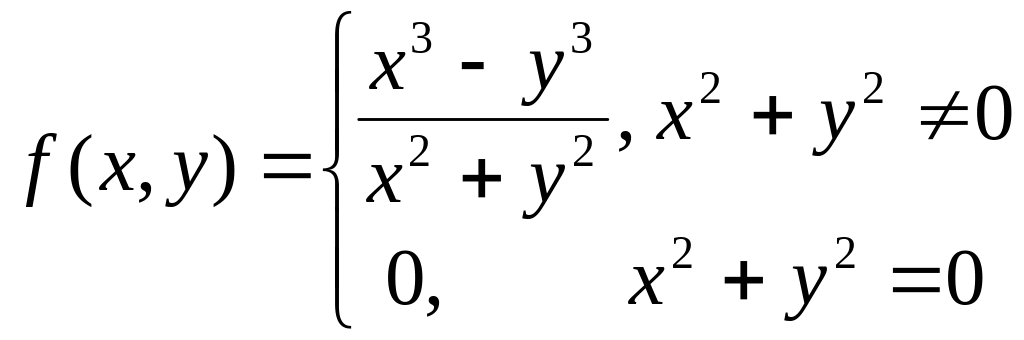 .
.Дайте определение частных производных функции в точке . Найдите, исходя из определения, частные производные функции
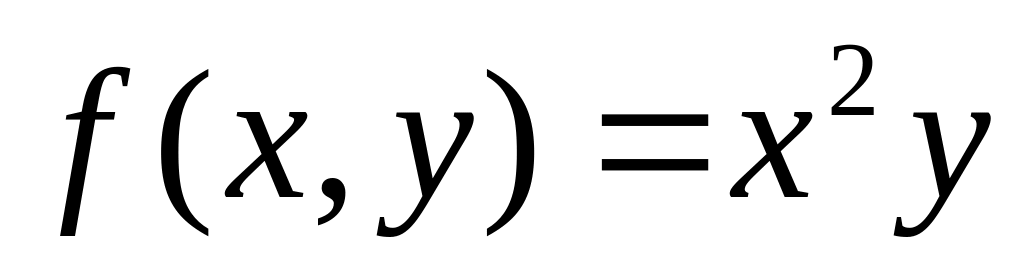 в точке
в точке
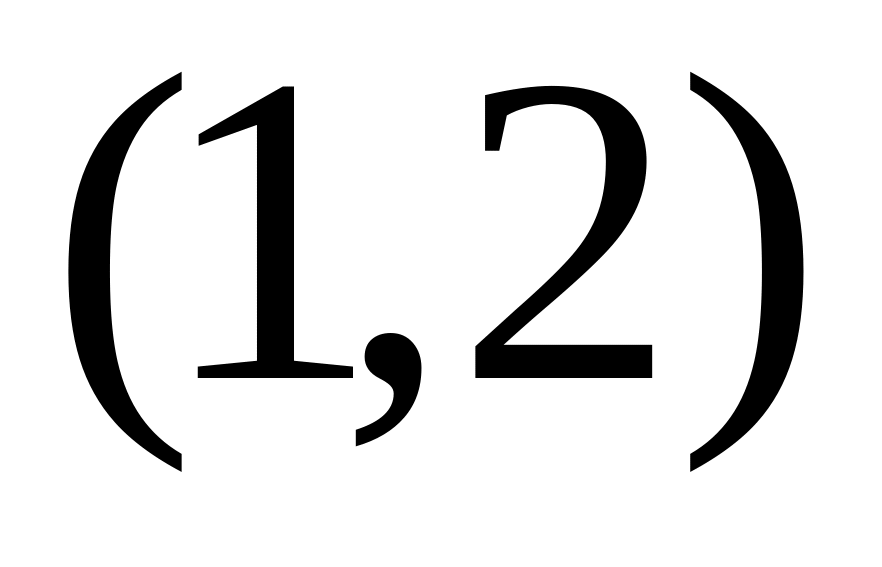 .
.
Дайте определение дифференцируемости функции в точке . Докажите, что если функция дифференцируема в точке , то она непрерывна в этой точке.
Дайте определение дифференциала функции в точке . Какая функция называется дифференцируемой в точке ? Приведите пример.
Как связаны производная по направлению и градиент дифференцируемой функции ? Чему равна производная по направлению, перпендикулярному градиенту?
Дайте определение градиента функции в точке . Докажите, что в направлении градиента происходит наиболее быстрый рост функции. Чему равна скорость этого роста?
Дайте определение однородной функции степени
 .
Является ли функция
.
Является ли функция
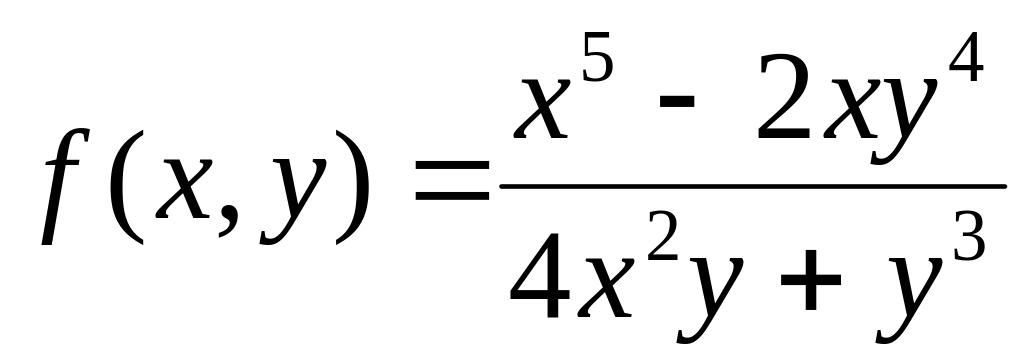 однородной? Если да, то какой степени?
однородной? Если да, то какой степени?Дайте определение однородной функции нескольких переменных. Приведите пример однородной функции степени 3, не являющейся рациональной функцией.
Дайте определение однородной функции степени . Выведите формулу Эйлера для однородной функции трех переменных.
Дайте определение локального экстремума функции двух переменных. Является ли равенство нулю частных производных функции в некоторой точке достаточным условием ее локального экстремума в этой точке?
Дайте определение локального экстремума функции двух переменных. Имеет ли функция
 локальный экстремум в точке
?
Ответ обоснуйте.
локальный экстремум в точке
?
Ответ обоснуйте.
Дайте определение локального экстремума функции двух переменных. Имеет ли функция
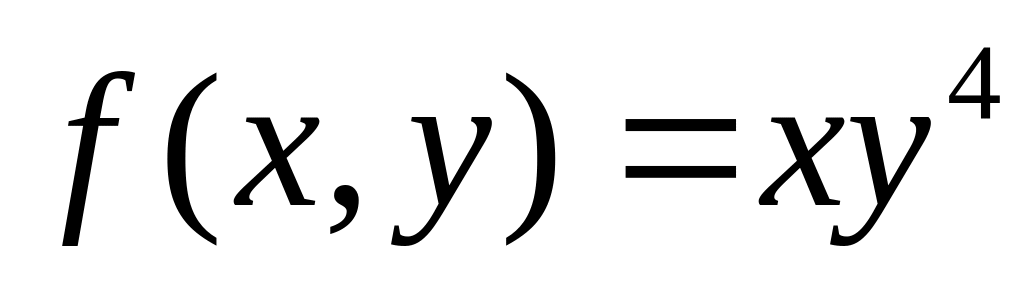 локальный
экстремум в точке
?
Ответ обоснуйте.
локальный
экстремум в точке
?
Ответ обоснуйте.Сформулируйте достаточное условие локального экстремума функции двух переменных. Имеет ли функция
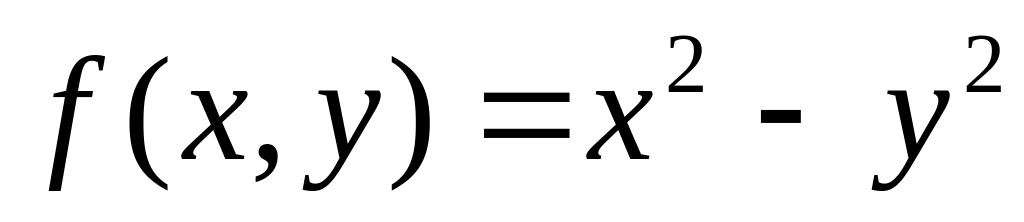 в точке
локальный экстремум? Ответ обоснуйте.
в точке
локальный экстремум? Ответ обоснуйте.
Докажите, что функция
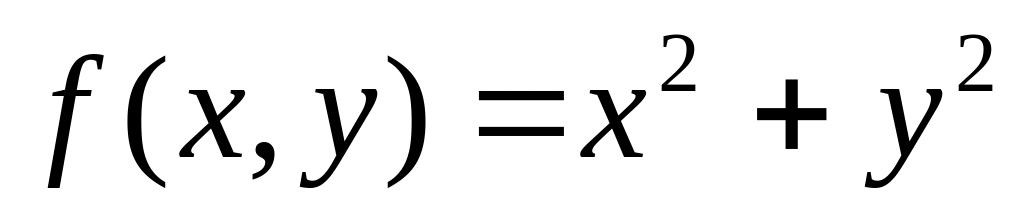 :
а) не имеет локального экстремума в
точке
:
а) не имеет локального экстремума в
точке
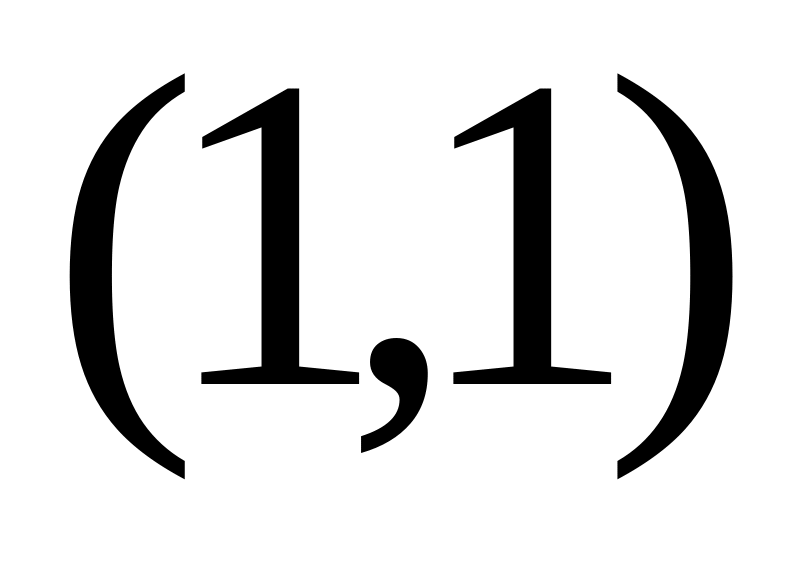 ,
б) имеет в этой точке условный локальный
экстремум при наличии связи
,
б) имеет в этой точке условный локальный
экстремум при наличии связи
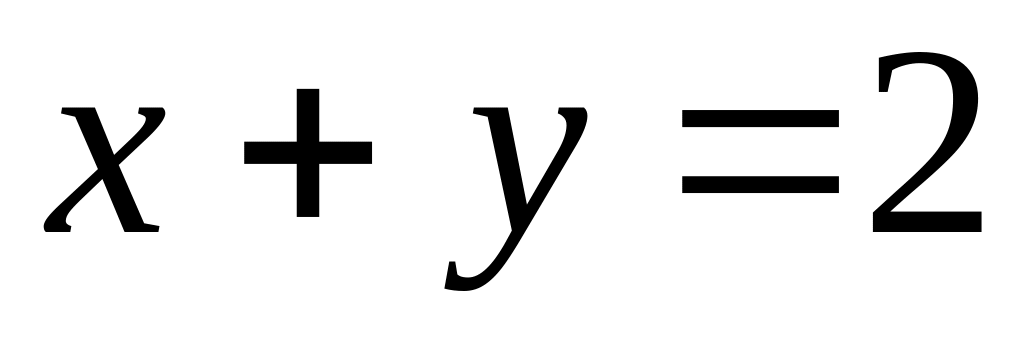 .
.Найдите наименьшее значение функции
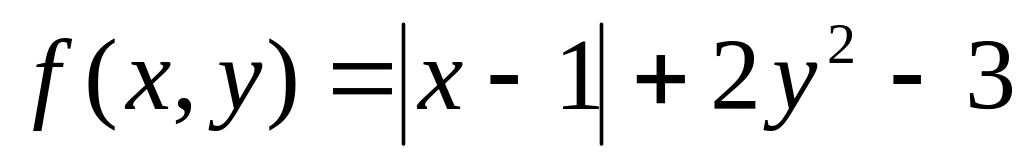 .
.Рассмотрев линии уровня функции , выяснить, в каких точках круга
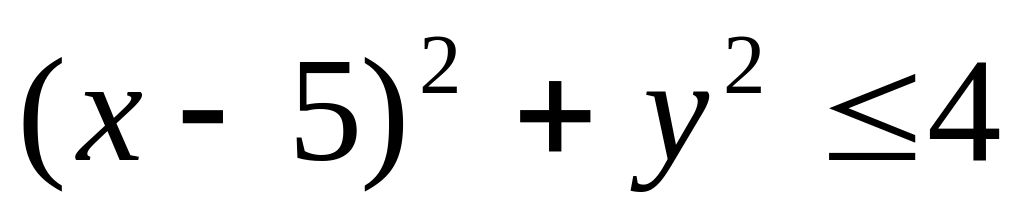 она принимает наибольшее и наименьшее
значения, найти эти значения.
она принимает наибольшее и наименьшее
значения, найти эти значения.
