
- •Теоретическая механика
- •260601– Машины и аппараты пищевых производств
- •Содержание
- •1. Общие методические рекомендации по изучению курса
- •1.1. Цели и задачи курса
- •1.2 Рекомендуемая литература
- •1.3 Методические указания по изучению курса
- •1.4. Учебная программа
- •Статика твердого тела
- •Кинематика
- •Кинематика твердого тела
- •Динамика
- •Динамика точки.
- •Общие теоремы динамики
- •1.5. Контрольные задания Содержание заданий, выбор вариантов, порядок выполнения работ, пояснения к тесту задач
- •2 Статика твердого тела
- •2.1 Основные понятия
- •2.2 Связи и их реакции
- •2.3 Момент силы относительно точки
- •2.4. Векторный момент силы относительно центра
- •2.5 Момент силы относительно оси
- •2.6. Пара сил
- •2.7. Приведение системы сил к заданному центру
- •2.8 Равновесие твердого тела
- •2.9 Последовательность решения задач о равновесии
- •2.10 Контрольные задания
- •Задача с1
- •Задача с2
- •Задача с3
- •3 Кинематика
- •3.1 Кинематика точки
- •3.1.1 Способы задания движения
- •3.1.2 Скорость и ускорение точки
- •3.1.3 Частные случаи движения точки
- •3.1.4 Последовательность решения задач по кинематике точки
- •Задача к1
- •3.2 Поступательное и вращательное движения твердого тела
- •3.2.1 Поступательное движение твердого тела
- •3.2.2 Вращение твердого тела вокруг неподвижной оси Угловая скорость и угловое ускорение
- •3.2.3 Траектории, скорости и ускорения точек вращающегося тела
- •3.2.4 Векторные формулы для скоростей и ускорений точек тела
- •3.3 Сложное движение точки
- •3.3.1 Теорема о сложении скоростей
- •3.3.2 Ускорение точки в сложном движении
- •Задача к2
- •3.4 Плоскопараллельное движение твердого тела
- •3.4.1 Уравнение плоскопараллельного движения
- •3.4.2 Графоаналитические методы определения скоростей точек плоской фигуры
- •Мгновенный центр скоростей (мцс)
- •3.4.3 Определение угловой скорости при плоском движении
- •3.4.4 Графоаналитические методы определения ускорений точек плоской фигуры
- •3.4.5 Определение углового ускорения при плоском движении
- •Задача кз
- •4. Динамика
- •4.1 Законы Ньютона – Галилея
- •4.2 Дифференциальные уравнения движения материальной точки. Первая и вторая задачи динамики.
- •Задача д1.
- •4.3 Механическая система. Основные понятия.
- •4.4 Кинетические характеристики движения механической системы.
- •1. Количество движения.
- •2. Главный момент количества движения или кинетический момент механической системы.
- •3.Кинетическая энергия.
- •4.5 Общие теоремы динамики точки и механической системы. Теорема о движении центра масс системы.
- •4.6 Теорема об изменении количества движения материальной точки и механической системы.
- •4.7 Теорема об изменении количества движения механической системы.
- •Закон сохранения количества движения
- •4.8 Теорема об изменении кинетического момента
- •4.9 Закон сохранения кинетического момента системы
- •Задача д2
- •4.10 Теорема об изменении кинетической энергии
- •4.11. Теорема об изменении кинетической энергии системы
- •Задача д3
- •4.12. Принцип Даламбера
- •4.13. Принцип Даламбера для механической системы.
- •Задача д4
- •4.14 Принцип возможных перемещений и общее уравнение динамики.
- •4.15 Принцип Даламбера – Лагранжа
- •Задача д5
- •Вопросы к экзамену
- •Часть 1. Статика твердого тела
- •Часть 2. Кинематика.
- •Часть 3. Динамика.
3.2.4 Векторные формулы для скоростей и ускорений точек тела
Скорость точки по модулю и направлению можно определить по формуле Эйлера векторным произведением:

![]() (3.28)
(3.28)
где
![]() –
радиус-вектор точки М,
проведенной из произвольной точки оси
вращения Oz,
например точки О
(рис. 3.10). В справедливости формулы (3.28)
можно убедится определив по ней модуль
скорости.
–
радиус-вектор точки М,
проведенной из произвольной точки оси
вращения Oz,
например точки О
(рис. 3.10). В справедливости формулы (3.28)
можно убедится определив по ней модуль
скорости.
![]()
Из определения ускорения и векторной формулы Эйлера имеем:
Рис. 3.10
Касательное и нормальное ускорения также можно записать в виде:
![]()
где
![]() –
соответственно ортогональные единичные
векторы (см. выше 3.1.2).
–
соответственно ортогональные единичные
векторы (см. выше 3.1.2).
Рассмотрим конкретные задачи.
Задача 3.1 Ротор мотора в период пуска имеет угловое ускорение = 2 с–2. Определить скорость, касательное, нормальное и полное ускорения точки М (рис. 3.11), лежащей на ободе ротора в момент t = 3 c. Диаметр ротора d = 0,2 м.
Решение
Угловую скорость ротора в момент времени t = 3 c находим, пользуясь формулой (3.25):
= о + t
З десь
и далее учитываем, что вращение ротора
равноускоренное, начальный угол поворота
о= 0 и начальная
угловая скорость о
= 0, так как ротор начинает вращаться
из состояния покоя. Тогда
= t
= 23 = 6
с–2. Для определения положения
точки на ободе ротора вычислим также
по формуле (3.24) угол поворота
десь
и далее учитываем, что вращение ротора
равноускоренное, начальный угол поворота
о= 0 и начальная
угловая скорость о
= 0, так как ротор начинает вращаться
из состояния покоя. Тогда
= t
= 23 = 6
с–2. Для определения положения
точки на ободе ротора вычислим также
по формуле (3.24) угол поворота
![]() По формулам (3.27) определим соответственно
скорость, касательное, нормальное и
полное ускорение точки М.
По формулам (3.27) определим соответственно
скорость, касательное, нормальное и
полное ускорение точки М.
Рис. 3.11
Векторы
![]() в момент времени t
= 3 c
изображены на рисунке 3.11.
в момент времени t
= 3 c
изображены на рисунке 3.11.
Задача
3.2 В период
разгона маховика закон его вращения
характеризуется
![]() .
Определить скорость и ускорение точки,
находящейся на расстоянии
R
= 0,8 м от оси
вращения в тот момент, когда касательное
и нормальное ускорения точки равны.
.
Определить скорость и ускорение точки,
находящейся на расстоянии
R
= 0,8 м от оси
вращения в тот момент, когда касательное
и нормальное ускорения точки равны.
Решение
По формулам (3.21) и (3.22) определяем угловую скорость и угловое ускорение маховика.
![]()
Касательное
и нормальное ускорения соответственно
равны a
= R,
an
= 2R.
По условию задачи в момент времени t
= t1
a
= an.
Поэтому в этот момент
= 2
или
![]() откуда
откуда
![]() Подставляя t1
в выражения для
и ,
находим, что в момент времени t1
Подставляя t1
в выражения для
и ,
находим, что в момент времени t1

Определим скорость и полное ускорение при t = t1
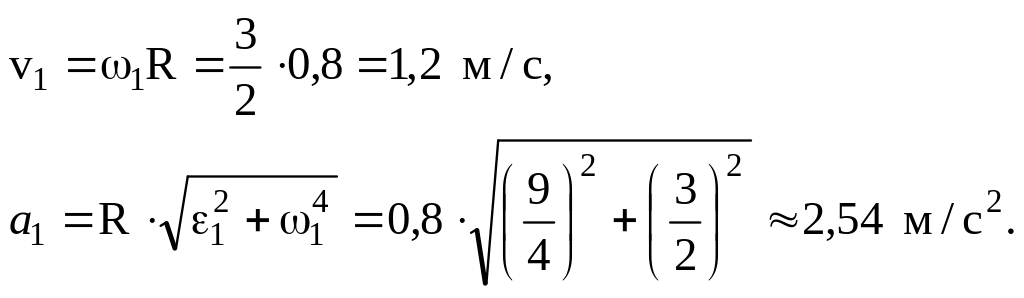
Задача 3.3 Шестерня 1 радиуса r1 приводится во вращение рукояткой АО1 = l. Эта шестерня сцеплена зубчатым колесом 2 радиуса r2, которое наглухо насажено на вал диаметра d. На вал намотан нерастяжимый канат, к которому прикреплен груз В. Определить скорость и ускорение груза В, если рукоятка АО1, вращаясь равноускоренно из состояния покоя совершает 16 оборотов за 2 с после начала движения (рис. 3.12).
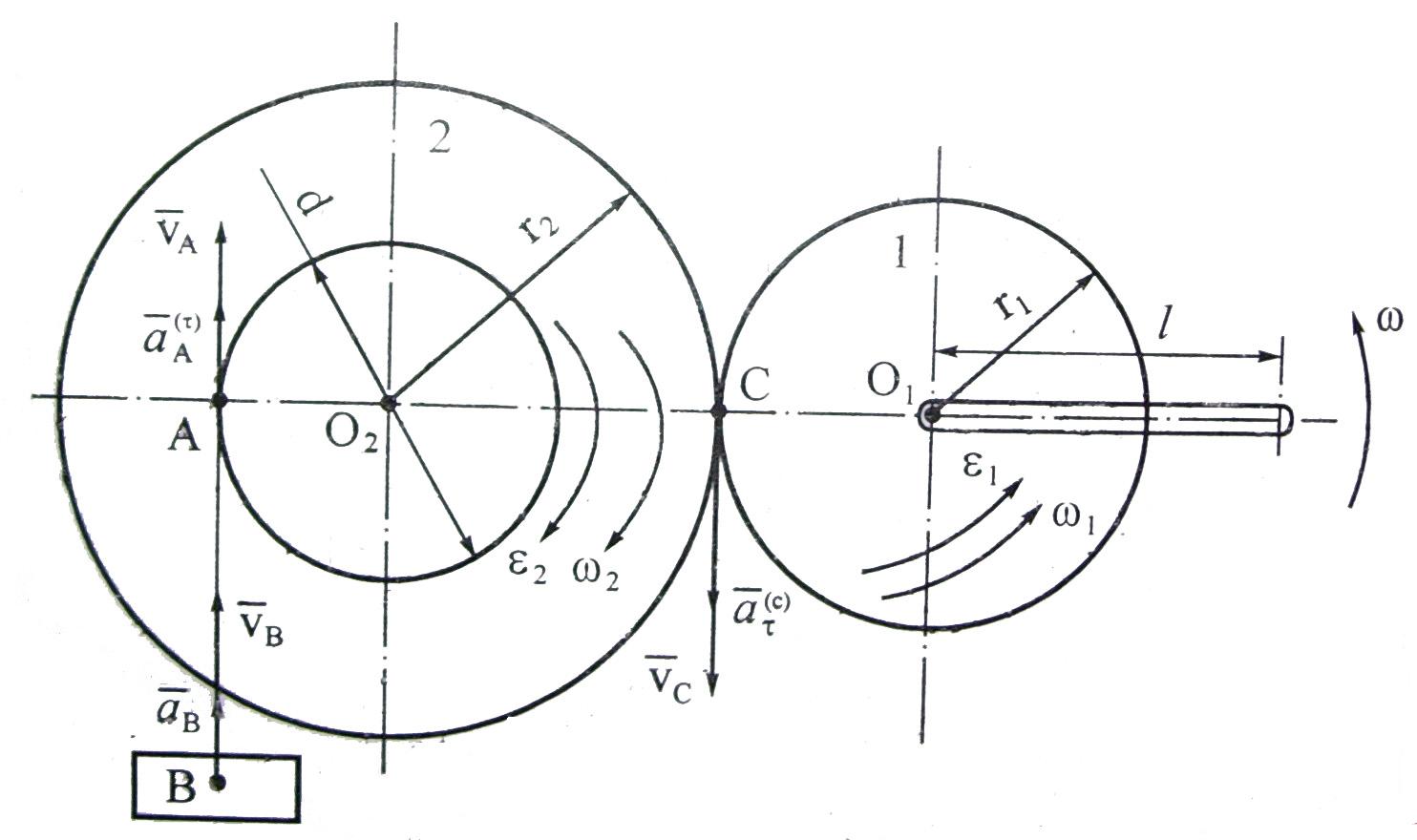
Р
Рис. 3.12
Определяем
угловое ускорение из формулы (3.25). По
условию задачи о
= 0,
о
= 0,
![]() .
Отсюда
.
Отсюда
![]()
Угловую скорость рукоятки для t = 2 с определяем по формуле (3.25) при о = 0: = t = 162 = 32 c–1.
Угловая скорость шестерни 1 равна угловой скорости рукоятки, так как они неизменно связаны между собой:
1 = = 32 с–1
Скорость точки С, которая принадлежит к шестерне 1 и колесу 2, равна
vC
= 1r1
= 2r2
, откуда
![]()
Касательное
ускорение а(С)
точки С
находится по формуле (3.27)
а(С)
= 1r1=
2r2
. Откуда
![]() Так как колесо 2
и вал жестко скреплены, имеем:
Так как колесо 2
и вал жестко скреплены, имеем:
![]()
Поскольку канат нерастяжим и вместе с грузом совершает поступательное движение, можно определить

