Чорноморський державний університет ім. П. Могили

Кафедра філософії

Логіка: приклади розв’язання задач:

методична розробка.

Укладач – ст. викл. кафедри філософії

Маргеліс Наталія Володимирівна

Миколаїв - 2009

Логіка: приклади розв’язання задач. Методична розробка для студентів денної та заочної форми навчання / Укладач – Маргеліс Н.В.

Рецензенти: канд. філософ. наук, професор ПСІ КСУ Хімченко О.Г.

доктор філософ. наук, проф. ЧДУ ім.. П.Могили Гавеля В.Л.

Затверджено на засіданні кафедри протокол № _8___ від 06.03.2009 р.

ЗМІСТ

ВСТУП.

1.ПРИКЛАДИ РОЗВ’ЯЗАННЯ ВПРАВ ЗА ТЕМОЮ «ПОНЯТТЯ».

2. ПРИКЛАДИ РОЗВ’ЯЗАННЯ ВПРАВ ЗА ТЕМОЮ «СУДЖЕННЯ».

3. ПРИКЛАДИ РОЗВ’ЯЗАННЯ ВПРАВ ЗА ТЕМАМИ «УМОВИВІД» І «ЗАКОНИ ЛОГІКИ».

4. ПРИКЛАДИ РОЗВ’ЯЗАННЯ ЗАДАЧ ДО ТЕМИ «ДОВЕДЕННЯ І СПРОСТУВАННЯ МІРКУВАНЬ».

СЛОВНИК БАЗОВИХ ТЕРМІНІВ.

ЛІТЕРАТУРА.

ВСТУП

Вивчення логіки має за мету формування навичок правильного мислення та вміння їх застосувати для подальшого успішного оволодіння суспільними та фаховими дисциплінами, в практичній діяльності взагалі. В результаті вивчення логіки необхідно

знати:

• предмет дисципліни, її структуру та понятійний апарат;

• основні логічні форми та закони правильного мислення;

• логічні операції над поняттями та судженнями;

• основні види умовиводів;

• основи логічної теорії доведення та спростування.

уміти:

• давати правильні визначення поняттям та термінам;

• аналізувати та формалізувати вербальні висловлювання;

• робити безпосередні та опосередковані умовиводи;

• логічно обґрунтовувати правильні твердження та спростовувати неправильні;

• знаходити логічні помилки у визначеннях, умовиводах та доведеннях.

Для успішного оволодіння програмними знаннями з логіки студенту треба вміти розв’язувати вправи, які є необхідною умовою формування навичок правильного мислення та застосування їх в житті.

В методичну розробку включені приклади розв’язання задач з усіх тем, а також словник базових термінів та необхідна література.

1. Приклади розв’язання вправ за темою «поняття» Вправа 1.

Визначте зміст, обсяг, підкласи обсягу й елементи обсягу (якщо є) в таких поняттях:

а) планета Сонячної системи;

б) хімічний елемент;

в) русалка.

Приклади розв’язання:

а) Щоб розкрити зміст поняття “планета Сонячної системи”, необхідно дати його визначення; отже, планета Сонячної системи — це така планета, яка обертається навколо Сонця. Обсяг цього поняття складається з дев’яти елементів (планет, відомих сучасній науці). Підкласи обсягу: внутрішні (від Меркурія до Марса) і зовнішні (від Юпітера до Плутона) планети. Елементи обсягу: Меркурій, Венера, Земля, Марс, Юпітер, Сатурн, Уран, Нептун, Плутон.

б) Щоб розкрити зміст поняття “хімічний елемент”, необхідно дати його визначення; отже, хімічний елемент — це частина речовини, яку далі не можна поділити (атом у фізиці). У своєму визначенні ми абстрагуємося від тієї обставини, що атоми також складаються з частин: протонів, нейтронів та ін. Обсяг цього поняття — це елементи періодичної системи Д.І. Менделєєва. Підкласи обсягу: метали, гази, радіоактивні і тощо. Елементи обсягу: водень, гелій тощо.

в) Щоб розкрити зміст поняття “русалка”, необхідно дати його визначення; отже, русалка — це міфічна істота, верхня частина якої має людську подобу, а нижня — риб’ячу. Обсяг цього поняття — 0 (на сьогодні достовірних відомостей про їх існування немає). Підкласи обсягу: немає. Елементи обсягу: немає.

Вправа 2.

Наведіть приклади таких видів понять:

а) пустих і непустих;

б) збірних і незбірних;

в) конкретних і абстрактних;

г) позитивних і негативних, співвідносних і безвідносних.

Приклади розв’язання:

а) Пусті (в обсязі 0 елементів): квадратне коло, химера тощо. Непусті (в обсязі понад 0 елементів) бувають одиничними і загальними. Одиничні (в обсязі 1 елемент): столиця Волинської області, автор “Кобзаря”, творець теорії відносності тощо. Загальні (в обсязі більше одного елемента): місто на Дніпрі, киянин, апельсин, природнича наука та ін.

б) Збірні (елементами їх є множини): футбольна команда, галактика тощо. Незбірні (елементами їх є окремі предмети): футболіст, країна та ін.

в) Конкретні (мають як змістове значення, так і предметне): корова, стіл тощо. Абстрактні (мають лише змістове значення, тобто позначають лише

властивості): радість, натхнення та ін.

г) Позитивні (складаються з позитивних ознак або вказують на наявність певної ознаки): оптимальний варіант, справжній громадянин тощо. Негативні (вказують на відсутність певної ознаки): неохайний вигляд, іншомовний та ін. Співвідносні (їх зміст не має автономного смислу): причетність, діалог тощо. Безвідносні (їх зміст має самостійний смисл): КДУ ім. Т.Г. Шевченка, Дніпро, хліб та ін.

Вправа 3.

Дайте повну характеристику поняттю (за обсягом і змістом): скромність.

Приклад розв’язання:

Скромність - загальне, абстрактне, позитивне, безвідносне, незбірне, нереєструюче.

Вправа 4.

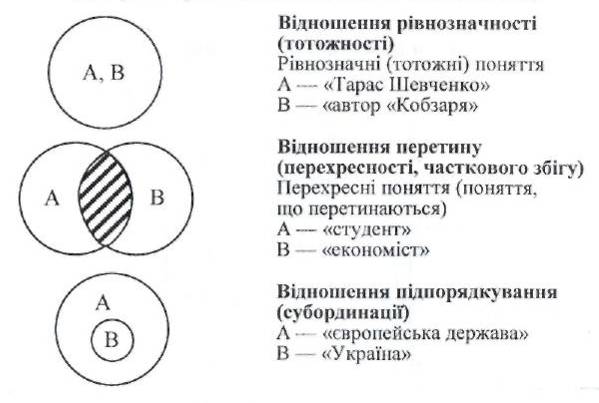
Наведіть приклади понять, обсяги яких перебувають між собою у відношеннях:

а) рівнозначності (тотожності);

б) перетину;

в) підпорядкованості;

г) співпідпорядкованості

д) протилежності (контрарності);

е) суперечності (контрадикторності);

Приклади розв’язання:

Вправа 5.

В изначте відношення між обсягами понять, графічно зобразивши їх за допомогою кіл Ейлера:

1-будинок,

2

1

- цегляний будинок,

3

2

дерев’яний будинок,

4

4

- одноповерховий будинок,

5

5

- двоповерховий будинок;

3

Вправа 6.

В изначте відношення між обсягами понять, графічно зобразивши їх за допомогою кіл Ейлера:

1 - навчальний заклад;

2 - Національна Академія наук України,

3 - університет,

4 – Чорноморський державний університет,

5 - технікум

Обсяги понять 2, 1 не містять спільних елементів. Поняття 3, 5 співпідпорядковані 1. Обсяг поняття 4 входить в обсяг поняття 3, отже, 3 підпорядковує 4.