- •Тверской государственный технический университет
- •Е.А. Панкратов, н.Ю. Старовойтова, т.Л. Кравец
- •Химия и физика полимеров
- •Часть 2
- •Глава I. Молекулярное строение полимеров
- •Зависимость свойств полимеров от топологии макромолекул
- •Конфигурация макромолекулы и конфигурационная изомерия
- •Конформация макромолекулы и конформационная изомерия
- •Внутримолекулярное вращение
- •Гибкость полимерной цепи
- •Количественные характеристики гибкости
- •Потенциальная энергия макромолекулы
- •Механическая модель молекулы
- •Ближние и дальние взаимодействия
- •Межмолекулярные взаимодействия
- •Глава II. Полимерные тела
- •Фазовые, агрегатные и физические состояния высокомолекулярных соединений
- •Кристаллическое состояние полимеров
- •Основные условия кристаллизации полимеров
- •Влияние различных факторов на скорость и глубину кристаллизации
- •Механизм кристаллизации
- •Кинетические особенности кристаллизации
- •Характер деформации кристаллических полимеров
- •Лиотропные и термотропные жидкокристаллические полимеры
- •Стеклообразное состояние
- •Характеристика состояния
- •Температура хрупкости и температура стеклования
- •Деформация стеклообразных полимеров и явление вынужденной эластичности
- •Высокоэластическое состояние полимеров
- •Особенности высокоэластического состояния
- •Два типа упругих тел и характер высокоэластической деформации
- •Термодинамическое рассмотрение природы упругих сил
- •Кинетическая теория высокоэластичности
- •Релаксационный характер процесса деформации эластомеров
- •Явление гистерезиса
- •Вязкотекучее состояние полимеров
- •Характеристика состояния
- •Температура текучести
- •Ориентация макромолекул при течении полимера. Структурная вязкость
- •Механическое стеклование. Химическое течение
- •Пластическая и общая деформация полимеров
- •Надмолекулярные структуры в полимерах
- •Глава III. Растворы полимеров
- •Общая характеристика
- •Разбавленные растворы полимеров
- •Теория Флори-Хаггинса
- •Качество растворителя и -точка
- •Уравнение Марка-Куна-Хувинка
- •Полуразбавленные растворы полимеров. Явления ассоциации и гелеобразования
- •Концентрированные растворы полимеров и расплавы
- •Характеристика концентрированных растворов
- •Пластификация полимеров. Пластификаторы
- •Основы термодинамики растворов полимеров
- •Самопроизвольный характер процессов растворения
- •Тепловой эффект процессов растворения
- •Модель полимерного раствора Флори-Хаггинса
- •Фазовые равновесия системы «полимер-растворитель»
- •Набухание и растворение полимеров
- •Методы исследования растворов полимеров
- •Методы определения средних молекулярных масс
- •Осмометрия
- •3.7.3. Эластоосмометрия
- •Криоскопия и эбулиоскопия
- •Вискозиметрия
- •Светорассеяние
- •Фракционирование. Гельпроникающая хроматография и седиментация
- •Метод концевых групп
- •Глава IV. Физические свойства полимеров
- •Прочность и долговечность
- •Механическая прочность
- •Долговечность
- •Механизм разрушения полимеров
- •Факторы, влияющие на прочность образца
- •Кинетика процесса разрушения
- •Адгезия и аутогезия
- •Основные понятия и определения
- •Теории адгезии
- •Влияние различных факторов на величину адгезии полимеров
- •Образование аутогезионной связи
- •Проницаемость полимеров
- •Сорбция и диффузия газов и жидкостей. Газопроницаемость
- •Влияние физических факторов на газопроницаемость полимера
- •Паропроницаемость
- •Электрические свойства полимеров
- •Классификация полимеров по электропроводности
- •Характер электропроводности
- •Электропроводность полимеров с сопряженными двойными связями
- •Полимеры как диэлектрики. Основные характеристики диэлектриков
- •Библиографический список
- •Химия и физика полимеров
- •Часть 2
- •Учебное пособие
- •170026, Г. Тверь, наб. А. Никитина, 22
Количественные характеристики гибкости
Отклонения от равновесного состояния на коротких участках цепи вызывают на длинных участках проявление такого свойства полимера, как гибкость.
Количественными характеристиками гибкости макромолекулы могут служить персистентная длина, статистический сегмент, среднеквадратичное расстояние между концами цепи, средний квадрат радиуса инерции макромолекулы.
Среднеквадратичное расстояние между концами цепи. Конформация полимерного клубка постоянно меняется, отклоняется от равновесной. Расстояние между концами цепи при этом меняется. Чтобы узнать, какое расстояние между концами цепи наиболее часто реализуется, надо взять все значения, полученные в ходе измерений, и поделить на число измерений – т.е. найти среднее значение (рис. 8):
![]() .
.
Средний квадрат радиуса инерции (рис. 8) находится по формуле
![]() ,
,
где
![]() –
средний квадрат расстояния между i-м
мономерным звеном цепи и ее центром
масс (суммирование ведется по всем
мономерным звеньям).
–
средний квадрат расстояния между i-м
мономерным звеном цепи и ее центром
масс (суммирование ведется по всем
мономерным звеньям).
![]() и
и
![]() определяют средние размеры макромолекулы.
Экспериментально их получают из данных
по измерению вязкости полимерных
растворов, коэффициентов диффузии или
седиментации, по угловой зависимости
интенсивности рассеянного излучения.
определяют средние размеры макромолекулы.
Экспериментально их получают из данных
по измерению вязкости полимерных
растворов, коэффициентов диффузии или
седиментации, по угловой зависимости
интенсивности рассеянного излучения.
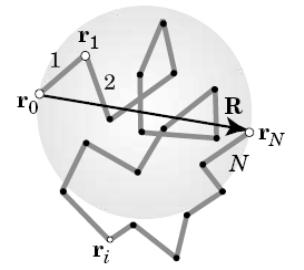

Рис. 4. Расстояние между концами цепи (слева) и радиус инерции (справа) в представлении свободно-сочлененной модели цепи
Зная длину жесткого
сегмента lN
и количество таких сегментов в цепи N,
можно рассчитать
![]() ,
используя разные приближения при
описании механизмов гибкости макромолекулы.
,
используя разные приближения при
описании механизмов гибкости макромолекулы.
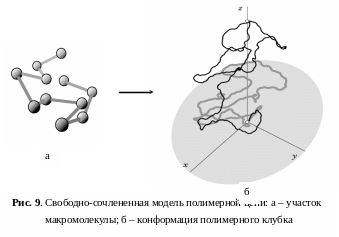
Свободно-сочлененная модель. Полимерная цепь представляется в виде отрезков – сегментов, моделирующих жесткий участок цепи, последовательно соединенных шарнирными сочленениями (рис. 9). Вращение жестких участков на шарнирах свободно. Для такой модели
![]() .
.
Модель с фиксированными валентными углами b. Отличается от предыдущей модели тем, что между двумя соседними сегментами фиксируется угол. Вращение вокруг осей остается свободным. В таком случае
![]() .
.
Поворотно-изомерная
модель. В
этой модели, кроме фиксированных
валентных углов, появляется заторможенное
внутреннее вращение, определяемое
величиной торсионного угла
![]() :
:
![]() .
.
Для идеального
клубка, зная
![]() ,
можно легко вычислить
,
можно легко вычислить
![]() :
:
![]()
 .
.
Средние размеры макромолекулы также можно выразить через контурную длину цепи L. Контурная длина цепи определяется числом мономерных звеньев или СПЗ, образующих макромолекулу. Если поделить цепь на жесткие участки равной длины, то
![]() . (1)
. (1)
Отсюда можно записать, используя свободно-сочлененную модель:
![]() , (2)
, (2)
![]() .
.
Такая модель справедлива для оценки термодинамической гибкости макромолекул гибкоцепных полимеров (lN 100 Å или 10 нм).
Из выражений (1), (2) можно найти величину наименьшего жесткого участка цепи (сегмента Куна):
![]() . (3)
. (3)
Исходя из выражения (3), для объема клубка можно записать:
![]() .
.
Гауссово распределение расстояний между концами цепи
Типичная конформация полимерного клубка имеет очевидное сходство с траекторией движения броуновской частицы (рис. 9б).
Вектор r, определяющий расстояние между концами цепи, сильно флуктуирует из-за теплового движения. Рассмотрим распределение вероятности вектора r между концами цепи из N сегментов для свободно-сочлененной модели идеальной цепи. Так как каждый сегмент дает независимый вклад в r, то, по аналогии с траекторией броуновской частицы, для величины r будет справедливо гауссово распределение (поэтому идеальный клубок часто называют гауссовым клубком):
 ,
,
где
![]() – средний размер клубка.
– средний размер клубка.
Таким образом,
наибольшему числу конформаций
соответствует не полностью свернутая
(R
= 0) или
выпрямленная (R
= L)
цепь, а некое промежуточное значение.
Для свободно-сочлененной цепи
![]() .
.
Гауссово распределение графически изображено на рис. 10.