Аналитическое продолжение вдоль пути

Построение продолжения относительно цепочки областей дискретно. В некотором роде в теории аналитического продолжения нам сейчас нужно осуществить переход, который равносилен переходу от последовательности к функции. Рассмотрим канонический элемент с центром в точке и некоторую непрерывную жорданову кривую , обладающую свойством . Для краткости обозначим .Предположим, что существует семейство канонических элементов с ненулевыми радиусами сходимости, такое, что  — центр элемента и для произвольного существует такая окрестность (понимаемая в смысле окрестностей на вещественной прямой), удовлетворяющая условию ; тогда, если для любого элемент является непосредственным продолжением элемента , то считается, что элемент таким образом аналитически продолжается вдоль пути .Выбирать семейство областей можно произвольным образом, так как можно доказать, что результат аналитического продолжения не зависит от выбора семейства областей.Достаточно интересным свойством обладает также функция  — радиус круга сходимости . Для семейства, упомянутого в определении продолжения вдоль пути, функция будет непрерывна в смысле вещественного анализа на .Собственно, осталось связать определение аналитического продолжения через цепочку областей и аналитического продолжения вдоль пути. Это очень просто. Допустим, что канонический элемент получен из элемента путем аналитического продолжения вдоль некоторого пути через промежуточное семейство элементов . Тогда, если выбрать некоторую возрастающую последовательность элементов отрезка , где круги и будут пересекаться, то элемент будет аналитическим продолжением элемента через цепочку областей .

Полная аналитическая функция

Развив аппарат аналитического продолжения вдоль путей, теперь можно перейти от изначальной аналитической функции через аналитические и канонические элементы к более общему понятию — полной аналитической функции. Таким термином будет обозначаться совокупность всех канонических элементов, получаемых из какого-либо первоначального элемента методом аналитического продолжения относительно всех возможных жордановых кривых, допускающих такое продолжение и берущих начало в точке  — центре элемента .

Немного проясняет внутреннее устройство такого весьма абстрактного понятия теорема Пуанкаре — Вольтерры, гласящая, что в каждой точке своей области определения полная аналитическая функция может иметь не более чем счетное множество элементов с центром в этой точке.

Важность понятия полной аналитической функции состоит в том, что оно позволяет с более общей точки зрения изучить понятие особой точки. А именно, особые точки для полной аналитической функции — просто точки границы области её определения. В зависимости от поведения функции в окрестности этих точек определяется их характер.

Рассмотрим некоторую особую точку для полной аналитической функции и некоторую её проколотую окрестность , принадлежащую области определения . Теперь выберем какую-нибудь замкнутую жорданову кривую . Если аналитическое продолжение вдоль кривой приводит к тому же элементу, то точка называется особой точкой однозначного характера и интерпретируется, как просто изолированная особая точка; если же результатом аналитического продолжения будет уже другой элемент, то точка называется особой точкой многозначного характера или точкой ветвления.

Принцип максимума модуля

Формулировка

Если голоморфна в некоторой области и существует точка такая, что во всей области выполняется неравенство , то .

Другими словами, модуль аналитической функции, отличной от константы, не может иметь локальных максимумов внутри области .

Следствия

• Принцип минимума модуля. Если аналитична в некоторой области , не обращается там в нуль и существует точка такая, что во всей области выполняется неравенство 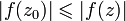, то . (То есть локальные минимумы модуля аналитической функции, отличной от константы, могут достигаться только в тех точках, где она обращается в ноль.)

• Принцип максимума вещественной и мнимой части. Если для аналитической функции в точке достигается локальный максимум (минимум) у её вещественной (или мнимой) части, тогда функция есть константа.

(Здесь используется обычный принцип максимума модуля для функций и , а также равенство .)

• Пусть  — компактное подмножество. Для всякой функции , непрерывной на и аналитичной внутри , выполнено равенство:

Если последовательность таких функций равномерно сходится на границе компакта , тогда она сходится равномерно на всём .