Министерство образования Республики Беларусь

Учреждения образования

«Гомельский государственный университет им Ф. Скорины»

Физический факультет

Смостоятельная учебная работа студента

По теме :

геометрическое приложение определённого интеграла

( площадь криволенейной трапеции, длинна дуги плоской кривой, объём тела вращения, площадь поверхности вращения )

Выполнила студентка группы Ф-15: Карпук Анна

Проверил преподаватель: Бородич Тимур Викторович

2011 г

Оглавление

Введение

Глава I. Задачи, приводящие к понятию определенного интеграла

Задачи о площади криволинейной трапеции

Глава II. Определенный интеграл как предел интегральной суммы

Глава III. Геометрический смысл определенного интеграла

Площадь криволинейной трапеции

Вычисление объема тела вращения

Вычисление площади поверхности вращения

Вычисление длины дуги

Вычисление длин кривых

Объёмы тел вращения

Площадь поверхности вращения

Введение

Интеграл(от лат. integer – целый), одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны, отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости этой точки), а с другой – измерять площади, объёмы, длины дуг, работу сил за определённый промежуток времени и т.п. Соответственно с этим различают неопределенные и определённые интегралы, вычисление которых является задачейинтегрального исчисления.

Определенный интеграл – одно из основных понятий математического анализа – является мощным средством исследования в математике, физике, механике и других дисциплинах.

Мы же рассмотрим геометрическое приложение определенного интеграла.

Объект курсового исследования: определенный интеграл.

Предмет курсового исследования: геометрическое приложение определенного интеграла.

Цель курсовой работы: показать применение определенного интеграла в геометрии

Глава I. Задачи, приводящие к понятию определенного интеграла

Пусть на промежутке [a; b] задана функция f(x)≥0. Криволинейной трапецией называется плоская фигура, ограниченная указанной кривой y=f(x), прямыми x=a, x=b и осью Оx. (рис. 1). Для вычисления ее площади проделаем несколько операций.

Рисунок 1

1). Разобьем промежуток [a; b] произвольными точками x₀=a<x₁<x₂<…<x_i-1<x_i<…<x_n=b на n частей. Положим Δx_i = x_i – x_i-1, то есть Δx_i есть длина i-го частичного отрезка, а наибольшую из этих длин обозначим λ, (λ=max Δx_i).

2). На каждом отрезке [x_i-1, x_i] возьмем по произвольной точке c_i,

x_i-1<c_i< x_i и вычислим f(c_i). Построим прямоугольник с основанием [x_i-1, x_i] и высотой f(c_i). Его площадь равна S_i=f(c_i)*(x_i – x_i-1). Проделаем это для каждого i = 1, 2, …, n.

3). Площадь всей заштрихованной ступенчатой фигуры, составленной из прямоугольников, равна сумме

.

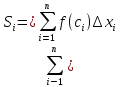Площадь S криволинейной трапеции будет приближенно равна площади ступенчатой фигуры:

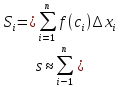
Чем мельче отрезки деления, тем точнее полученная фигура “отображает” криволинейную трапецию.

4). За площадь криволинейной трапеции принимают предел, к которому стремятся площади ступенчатых фигур, когда длины отрезков деления стремятся к нулю, а их число неограниченно увеличивается (n→∞). Таким образом,

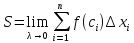
Мы рассмотрели несколько видов задач, приводящие к понятию определенного интеграла, а теперь сформулируем определения данного понятия. Возможны два различных подхода к определению определённого интеграла.

Определение 1: приращение F(b)-F(a) любой из преобразованных функций F(x)+c при изменении аргумента от x=a до x=b называют определённым интегралом от a до b функции f и обозначается .

Причём функция F является первообразной для функции f на некотором промежутке D, а числа а и b принадлежат этому промежутку. Это можно записать следующим образом:

Данная формула является формулой Ньютона-Лейбница.

Определение 2:

Рисунок. 2

Если при любой последовательности разбиений отрезка [a;b] таких, что δ = max Δx_i→0 (n→∞) и при любом выборе точек интегральная сумма σ_k=f(ε_i) Δx_i стремится к одному и тому же конечному пределу А, то это число А и есть определённый интеграл, т.е.

lim_n→∞ σ_k = lim_δ→0 f (ε_i) Δx_i=A(2).

Где Δх_i = x_i - x_i-1 (i=1,2,…,n) ε = max Δx_i – начало разбиения произвольная точка из отрезка [x_i-1;x_i] сумма всех произведений f(ε_i)Δx_i(i=1,…,n). Простыми словами, определенный интеграл есть предел интегральной суммы, число членов которой неограниченно возрастает, а каждое слагаемое стремится к нулю.