1.3 Закон Фурье

Для передачи теплоты, как формы энергии, в любом теле необходимым условием есть наличие разности температур в различных точках тела. Очевидно, что это условие относится и к передаче теплоты теплопроводностью, при которой градиент температуры в различных точках тела не должен быть равен нулю ( ≠ 0).

Связь между количеством теплоты dQ, передаваемой теплопроводностью через элементарную площадку dF, расположенную на изотермной поверхности, за время dτ и градиентом температуры устанавливается гипотезой Фурье:

, Дж. (1.5)

Множитель пропорциональности λ в правой части называется коэффициентом теплопроводности.

Количество теплоты, проходящей через единицу изотермной поверхности в единицу времени, называют плотностью теплового потока или вектором плотности теплового потока, имеющим размерность [Вт/м²].

или . (1.6)

Эту запись гипотезы Фурье называют законом Фурье.

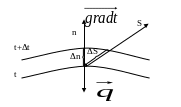
Рисунок 1.2 К определению вектора плотности теплового потока

Вектор плотности теплового потока считают положительным, если он направлен по нормали к изотермической поверхности в сторону убывания температуры. Вектор плотности теплового потока и вектор градиента температуры лежат на одной прямой, но вектор градиента температуры направлен в сторону возрастания температуры, поэтому в приведенных выше формулах в правой части стоит минус.

Как следует из закона Фурье, для определения количества теплоты, проходящей через произвольную поверхность тела, необходимо знать температурное поле внутри рассматриваемого тела. Нахождение температурного поля и составляет основную задачу аналитической теории теплопроводности.

1.4 Коэффициент теплопроводности. Физический смысл, зависимость от температуры

Коэффициент теплопроводности λ есть физический параметр вещества, характеризующий его способность проводить теплоту.

Размерность и физический смысл λ определяется из гипотезы Фурье:

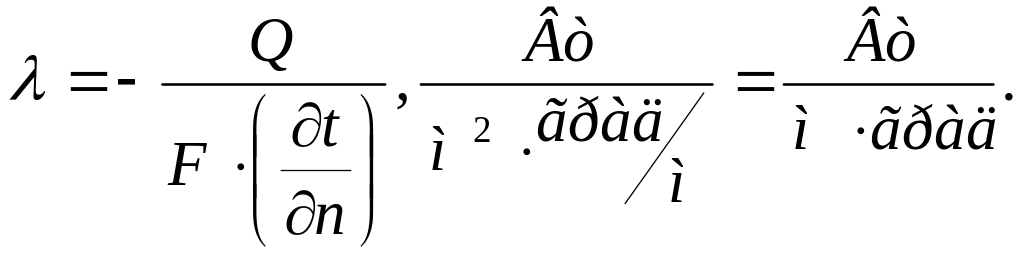(1.7)

Значение коэффициента теплопроводности λ определяет количество теплоты, проходящей через единицу изотермной поверхности в единицу времени, при условии, что градиент температуры равен единице.

В общем случае коэффициент теплопроводности зависит от температуры и давления.

Для многих твердых материалов зависимость λ от температуры может быть принята линейной:

λ = λ₀·[1 + b·(t – t₀)], (1.8)

где λ₀ – коэффициент теплопроводности при температуре t₀;

t – текущая температура;

b – коэффициент, определяемый опытным путем.

Наиболее теплопроводными являются металлы, у которых λ составляет 3÷468 Вт/м·град. Коэффициенты теплопроводности чистых металлов, за исключением алюминия, с возрастанием температуры убывают. Самым теплопроводным металлом является чистое серебро.

Коэффициенты теплопроводности сухих строительных и теплоизоляционных материалов при повышении температуры возрастают по линейному закону и изменяются в пределах от 0,01 до 3 Вт/м·град. Увеличение λ пористых материалов при повышении температуры объясняется значительным возрастанием лучистого теплообмена между поверхностями твердого «скелета» пор. Конвективная составляющая теплообмена в порах растет с увеличением размера пор. Коэффициенты теплопроводности отдельных видов материалов зависят от их объёмной массы (пористости), влажности и температуры. В основном эти зависимости определяются соотношением составляющих, которыми может быть заполнен объём материала.

Коэффициент теплопроводности любого материала сильно отличается от коэффициента теплопроводности воздуха   0,023 Вт/мград. Влага, заполняющая поры имеет   0,58 Вт/мград, т.е. в 25 раз больший, чем у воздуха. При переходе жидкой влаги в лед её теплопроводность увеличивается в 4 раза и для льда   2,3 Вт/мград. Важной для строительных материалов является зависимость  от влажности. С увеличением влажности материалов коэффициент теплопроводности возрастает.

С увеличением объёмной массы теплопроводность одного и того же материала заметно возрастает. Так, например, пенобетон при _o = 400 кг/м³ имеет  = 0,14 Вт/мград, при _o = 600 кг/м³ уже  = 0,21 Вт/мград, а при _o = 1000 кг/м³ – уже  = 0,4 Вт/мград.

Поэтому эффективный коэффициент теплопроводности пористых материалов имеет сложную природу и является условной величиной.

Коэффициенты теплопроводности большинства капельных жидкостей (λ = 0,08÷0,65 Вт/м·град) с повышением температуры убывают. Вода является исключением: с увеличением температуры от 0 до 127 ^оС коэффициент теплопроводности повышается, а при дальнейшем возрастании температуры уменьшается. От давления λ капельных жидкостей практически не зависят.

Коэффициенты теплопроводности газов (λ = 0,005÷0,6 Вт/м·град) при повышении температуры возрастают и практически не зависят от давления.

Коэффициенты теплопроводности различных веществ определяются опытным путем и для технических расчетов берутся по справочным данным.